حتماً میدانید که حل یک تست بدون در اختیار داشتن پاسخنامه تشریحی ناممکن است؛ بنابراین شما باید جواب تشریحی تمامی تستهای کنکور ارشد کامپیوتر را داشته باشید. در این مقاله به روشهایی اشاره میکنیم که با استفاده از آنها میتوانید به پاسخ تشریحی کنکور ارشد کامپیوتر ۱۳۹۰ دسترسی داشته باشید. نحوه دسترسی به پاسخ کلیدی کنکور کامپیوتر ۱۳۹۰ نیز در انتهای مقاله بیان شده است.
آسان
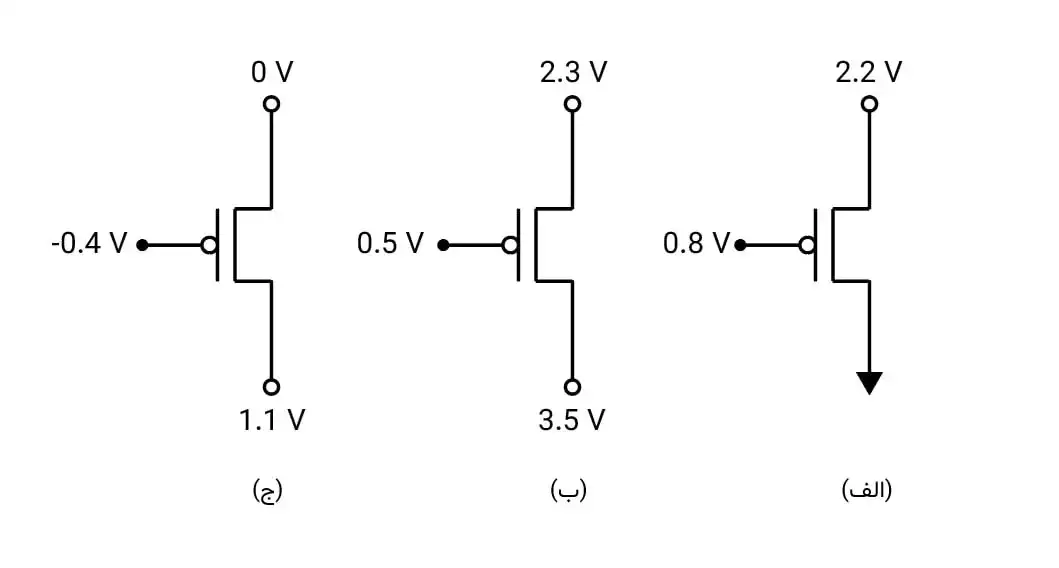
با فرض آن که مقدار ولتاژ آستانه برای ترانزیستور pMOS برابر -0.4 V باشد، کدام گزینه وضعیت صحیح بایاس را برای هر سه حالت (الف)، (ب) و (ج) درست نشان داده است؟
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
1 (الف) = (ب) = خطی و (ج) = اشباع
2 (الف) = اشباع، (ب) = خطی و (ج) = نقطه مرزی اشباع و خطی
3 (الف) = (ج) = اشباع و (ب) = خطی
4 (الف) = اشباع، (ب) = قطع و (ج) = نقطه مرزی اشباع و خطی
گزینه 2 صحیح است.
ترانزیستور PMOS روشن است اگر:
$V_{SG}>\left|V_{tp}\right|=0.4$
اگر ترانزیستور PMOS روشن باشد شرط خطی و اشباع بودن آن به شرح زیر است:
$V_{SD}<V_{SG}-\left|V_{tp}\right|\to Triod$
$V_{SD}>V_{SG}-\left|V_{tp}\right|\to Saturated$
سر Source ترانزیستور آن سری است که ولتاژ بیشتری دارد.
مدار الف) اشباع
$V_{SG}=2.2-0.8=1.4V,\ V_{SD}=2.2V$
$\to V_{SG}>0.4,\ 2.2=V_{SD}>V_{SG}-\left|V_{tp}\right|=1.4-0.4=1\to Saturated$
مدار ب) خطی
$V_{SG}=3.5-0.5=3V,\ V_{SD}=3.5-2.3=1.2V$
$\to V_{SG}>0.4,\ 1.2=V_{SD}<V_{SG}-\left|V_{tp}\right|=3-0.4=2.6\to Triod$
مدار ج) نقطه مرزی اشباع و خطی
$V_{SG}=1.1+0.4=1.5V,\ V_{SD}=1.1V$
$\to V_{SG}>0.4,\ 1.1=V_{SD}=V_{SG}-\left|V_{tp}\right|=1.5-0.4=1.1\to Saturated\ or\ Triod$
روش های دسترسی به پاسخ نامه تشریحی تست های کنکور ارشد کامپیوتر ۱۳۹۰
برای دسترسی به پاسخ تشریحی تستهای کنکور ارشد کامپیوتر سال ۱۳۹۰ و سالهای دیگر میتوانید از دو روش زیر استفاده کنید.
روش اول: استفاده از پلتفرم آزمون کنکور کامپیوتر
شما با تهیه پلتفرم آزمون با یک تیر چند نشان میزنید. این پلتفرم علاوه بر پوشش پاسخنامه تشریحی تمامی تستهای کنکور کامپیوتر، آیتی و علوم کامپیوتر، میتوانید آزمون شخصیسازیشده بسازید، با دیگر دانشجویان رقابت کنید و…. برای آشنایی بیشتر با این پلتفرم به صفحه پلتفرم آزمون مراجعه کنید.
در زیر پاسخ تشریحی تست های کنکور کامپیوتر ۱۳۹۰ برای درسهای هوش مصنوعیدرس هوش مصنوعی این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده، سیستم عاملمعرفی درس سیستم عامل – بهترین آموزش درس سیستم عامل در کشور
این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده، سیستم عاملمعرفی درس سیستم عامل – بهترین آموزش درس سیستم عامل در کشور درس سیستم عامل در این صفحه معرفی شده، همچنین بهترین آموزش درس سیستم عامل در کشور را میتوانید در این صفحه تهیه کنید، فصول و مراجع سیستم عامل نیز بررسی شده، الکترونیک دیجیتالمعرفی درس الکترونیک دیجیتال
درس سیستم عامل در این صفحه معرفی شده، همچنین بهترین آموزش درس سیستم عامل در کشور را میتوانید در این صفحه تهیه کنید، فصول و مراجع سیستم عامل نیز بررسی شده، الکترونیک دیجیتالمعرفی درس الکترونیک دیجیتال درس الکترونیک دیجیتال در تمامی دانشگاههای جهان به منظور آشنایی با مبانی الکترونیک و سختافزار و تکنولوژیهای استفاده شده از زمان پیدایش کامپیوتر تا کنون تدریس میشود و نظریه زبان ها و ماشین هادرس نظریه زبان ها و ماشین ها
درس الکترونیک دیجیتال در تمامی دانشگاههای جهان به منظور آشنایی با مبانی الکترونیک و سختافزار و تکنولوژیهای استفاده شده از زمان پیدایش کامپیوتر تا کنون تدریس میشود و نظریه زبان ها و ماشین هادرس نظریه زبان ها و ماشین ها این صفحه عالی به معرفی درس نظریه زبانها و ماشینها پرداخته است، همچنین به اهمیت درس نظریه در کنکور ارشد کامپیوتر، سرفصلها، معرفی مراجع و فیلمهای آموزشی این درس پرداخته است. به همراه پاسخ تشریحی آمده است:
این صفحه عالی به معرفی درس نظریه زبانها و ماشینها پرداخته است، همچنین به اهمیت درس نظریه در کنکور ارشد کامپیوتر، سرفصلها، معرفی مراجع و فیلمهای آموزشی این درس پرداخته است. به همراه پاسخ تشریحی آمده است:
تست های درس هوش مصنوعی کنکور کامپیوتر ۱۳۹۰ به همراه جواب تشریحی
دشوار
چند مورد از موارد زیر درست میباشد؟
الگوریتم های جستجوی آگاهانه
1) اگر برای مسئله خاصی یک راهحل کامل ناآگاهانه وجود داشته باشد، آنگاه حداقل یک راهحل کامل آگاهانه نیز برای آن مسئله وجود دارد.
2) اگر برای مسئله خاصی حداقل یک راهحل کامل آگاهانه وجود داشته باشد، آنگاه حداقل یک راهحل کامل ناآگاهانه نیز برای آن مسئله وجود دارد.
3) اگر برای مسئله خاصی هیچ راهحل آگاهانهای وجود نداشته باشد، آنگاه هیچ راهحل کامل ناآگاهانهای نیز برای آن مسئله وجود ندارد.
4) اگر برای مسئله خاصی هیچ راهحل کامل ناآگاهانهای وجود نداشته باشد، آنگاه هیچ راهحل کامل آگاهانهای نیز برای آن مسئله وجود ندارد.
1 دو مورد
2 یک مورد
3 سه مورد
4 چهار مورد
گزینه 4 صحیح است.
اگر یک الگوریتم کامل باشد مستقل از این که آگاهانه است یا نه جواب را برمیگرداند همچنین اگر کامل نباشد هیچ جوابی را برنمیگرداند. پس اگر یک مسئله جواب داشت روشهای کامل آگاهانه و ناآگاهانه، هر دو میتوانند جواب را برگردانند و اگر جواب نداشت هر دو هیچ راه حلی برنمیگردانند. با توجه به توضیحات هر چهار مورد سوال درست است و جواب گزینه ۴ میباشد.
دشوار
روی یک توری n*n که هر خانه به چهار همسایه خود متصل است، خانه میانی را نقطه شروع جستجو و نقطه $\left(\circ \ ,\ \circ \right)$ در نظر میگیریم. گره هدف در موقعیت $\left(\mathrm{X\ ,\ Y}\right)$ است. در این گراف الگوریتم جستجوی A بدون تست تکراری بودن حالات، حداکثر $\left(\left({\mathrm{4}}^{\mathrm{X\ +\ Y\ +\ }\mathrm{1}}-\ \mathrm{1}\right)\ / \, \mathrm{3}\right)\mathrm{-}\mathrm{1}$ گره و الگوریتم جستجوی B با تست تکراری بودن حالات، حداکثر $\mathrm{2}\left(\mathrm{X\ +\ Y}\right)\left(\mathrm{X\ +\ Y\ +\ }\mathrm{1}\right)\ -\mathrm{1}$ گره را قبل از یافتن جواب بسط میدهند. کدام یک از گزینههای زیر در مورد این دو الگوریتم صحیح است؟
الگوریتم های جستجوی ناآگاهانه
1 A و B هر دو الگوریتم اول عمق (Depth first) هستند.
2 A و B هر دو الگوریتم اول پهنا (Breadth first) هستند.
3 A الگوریتم اول پهنا (Breadth first) و B الگوریتم اول عمق (Depth first) است.
4 A الگوریتم اول عمق (Depth first) و B الگوریتم اول پهنا (Breadth first) است.
گزینه 2 صحیح است.
(نکته : در این تست فرض شده است که تست در الگوریتم BFS در زمان بسط انجام میشود)
در این سوال در ابتدا هر کدام از حالات جستجو درختی و گرافی را با روش DFS و BFS بررسی میکنیم.
۱- جستجوی A بدون تست تکراری بودن حالات (درختی)
آ) BFS
در جستجو اول سطح در هر مرحله با توجه به اینکه هر گره چهار فرزند دارد، فاکتور انشعاب ۴ است (چون تکرار هم داریم) و در هر مرحله تعداد گرههای ۴ برابر میشود و در صورتی که بدانیم هدف در خانه (x,y)است داریم :
تعداد گرههای بسط داده شده $=\mathrm{1\ +\ b\ +\ }b^{2\ }+\ ......+b^{d\ }-1\ =\ \frac{b^{d+1}\ -1}{b-1}\ \ \ \ -1\ =\ \frac{4^{x+y+1}-1\ }{3}\ -1$
نکته :
۱- آخر برای کم کردن خود گره هدف است.
از آنجایی که در هر مرحله به یکی از گرههای مجاور میرویم و حرکت مورب نداریم میتوان گفت d = x +y میباشد.
ب) DFS
جستجو اول عمق در صورتی که تکرار داشته باشیم در بدترین حالت ممکن است در حلقه بینهایت بیفتد و هیچگاه تمام نشود.
۲- جستجوی A با تست تکراری بودن حالات (گرافی)
آ) BFS
در این جستجو مطابق شکل زیر در هر مرحله یک دور به مربع اضافه میشود تا به هدف که در (x,y) قرار دارد برسیم. تعداد گرههایی که در هر مرحله بسط داده میشوند الگویی مطابق فرمول زیر دارند:
تعداد گرههای بسط داده شده =
$ \mathrm{1+b+}2b+\dots \dots +\mathrm{bd\ -1}=1+4\left(1+2+\dots .+d\right)-1=1+\frac{4d\left(d+1\right)}{2}\ -1=2\left(x+y\right)\left(x+y+1\right)$
نکته :
۱- آخر برای کم کردن خود گره هدف است.
از آنجایی که در هر مرحله به یکی از گرههای مجاور میرویم و حرکت مورب نداریم میتوان گفت d = x +y میباشد.
ب) DFS
این روش در صورتی که تست تکراری بودن حالات را داشته باشیم در بدترین حالت همه گرههای صفحه یعنی $n^2-1$ گره را بررسی میکند.
با توجه به صورت سوال و با توجه به مقادیر که در بالا بدست آوردیم بهترین گزینه برای این پاسخ این سوال گزینه دوم است.
متوسط
کدامیک از گزینههای داده شده بازنمایی جملهی «هر دانشآموزی حداقل دو دوست دارد.» به منطق مرتبه اول است؟
منطق مرتبه اول
1 $\mathrm{\forall }\mathrm{x,\ y,\ student}\left(\mathrm{x}\right)\mathrm{\wedge }\mathrm{friend}\left(\mathrm{y\ ,\ x}\right)\mathrm{\Rightarrow }\mathrm{number}\left(\mathrm{y}\right)\mathrm{\ge }\mathrm{2}$
2 $\mathrm{\forall }\mathrm{x,\ y,\ student}\left(\mathrm{x}\right)\mathrm{\Rightarrow }\mathrm{number}\left(\mathrm{friend}\left(\mathrm{y\ ,\ x}\right)\right)\mathrm{\ge }\mathrm{2}$
3 $\mathrm{\forall }\mathrm{x,\ y,\ z,\ student}\left(\mathrm{x}\right)\mathrm{\wedge }\mathrm{friend}\left(\mathrm{y\ ,\ x}\right)\mathrm{\wedge }\mathrm{friend}\left(\mathrm{z\ ,\ x}\right)\mathrm{\Rightarrow }\mathrm{y\ }\mathrm{\neq }\mathrm{\ z}\mathrm{\ }$
4 $\mathrm{\forall }\mathrm{x,\ student}\left(\mathrm{x}\right)\mathrm{\Rightarrow }\mathrm{\exists }\mathrm{y,\ z,\ friend}\left(\mathrm{y\ ,\ x}\right)\mathrm{\wedge }\mathrm{friend}\left(\mathrm{z\ ,\ x}\right)\mathrm{\wedge }\mathrm{y\ }\mathrm{\neq }\mathrm{\ z}$
گزینه 4 صحیح است.
برای این سوال باید اثبات کنیم که هر دانشآموز باید دست کم دو دوست متفاوت داشته باشد.
گزینه ۲ و ۱: به طور کلی در منطق مرتبه اول هیچگاه از اعداد استفاده نمیکردیم پس این گزینه نادرست است.
گزینه ۳ : بخش اول این گزینه برای دانشآموزی که هیچ دوستی ندارد برابر F است که باعث میشود در کل این گزینه T شود که این مثال نقض باعث میشود که این گزینه نادرست شود.
گزینه ۴: این گزینه درست است و بیان میکند که یک نفر(x) یا دانشآموز نیست یا اگر دانش آموز است پس حتما دو نفر y,z وجود دارد که با x دوست هستند و y همان z نیز نیست.
دشوار
فرض کنید فضای جستجویی دارای پنج گره D ،C ،B ،A و
Eباشد. جدول زیر فواصل واقعی این گرهها را از هم نشان میدهد. (وجود عدد در هر خانه جدول نشاندهندۀ این است که از گره مربوط به سطر به سمت گره مربوط به ستون مسیری به طول عدد وجود دارد.) اگر گره A گره شروع، گره E گره هدف و تابع h تابع مکاشفهای تخمین فاصله گره تا هدف باشد، کدام یک از گزینههای زیر صحیح است؟
الگوریتم های جستجوی آگاهانه
| E |
D |
C |
B |
A |
|
| |
2 |
8 |
10 |
|
A |
| 2 |
|
2 |
|
10 |
B |
| 6 |
2 |
|
|
8 |
C |
| 9 |
|
2 |
|
2 |
D |
| |
9 |
6 |
2 |
|
E |
1 اگر h(c)=5 ، h(B)=1 و h(D)=8 ، آنگاه تابع h یک تابع یکنواخت (monotonic) و قابل قبول (admissible) است.
2 اگر h(c)=6 ، h(B)=3 و h(D)=9 ، آنگاه تابع h یک تابع یکنواخت (monotonic) و قابل قبول (admissible) است.
3 اگر h(c)=5 ، h(B)=1 و h(D)=8 ، آنگاه تابع h یک تابع یکنواخت (monotonic) نیست ولی قابل قبول (admissible) است.
4 اگر h(c)=3 ، h(B)=3 و h(D)=8 ، آنگاه تابع h یک تابع یکنواخت (monotonic) است ولی قابل قبول (admissible) نیست.
گزینه 3 صحیح است.
ابتدا گرافی که نشاندهنده فواصل داده شده در جدول است را رسم میکنیم سپس به بررسی گزینهها میپردازیم هم چنین میدانیم که یک هیوریستیک قابل قبول است اگر شرط $h \le h \ast$ برای همه گرههای آن برقرار باشد.
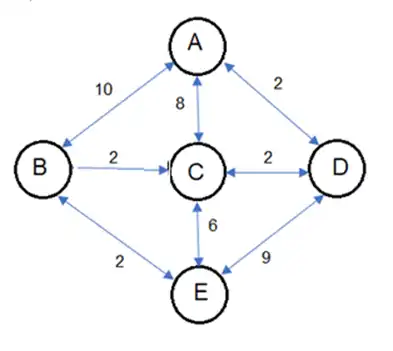
گزینه ۱ : در این گزینه h(C)=5, h(B)=1 , h(D)=8 داده شده است از طرفی با توجه به گراف بالا h*(C)=6, h*(B)=2 و h*(D)=8 میباشد پس شرط قابل قبول بودن برای این هیوریستیک برقرار است اما این هیوریستیک شرط سازگاری را ندارد چرا که برای مثال h(D) > h(C) + c(D,C) = h(C) + 2 میباشد پس این گزینه نادرست است.
گزینه ۲ : در این گزینه h(C)=6, h(B)=3 , h(D)=9 داده شده است مطابق گزینه قبل h*(C)=6, h*(B)=2 و h*(D)=8 میباشد پس شرط قابل قبول بودن برای این هیوریستیک برقرار نیست و در مورد سازگاری آن به دلیل اینکه داریم h(D) > h(C) + c(D,C) = h(C) + 2 این هیوریستیک ناسازگار است و این گزینه نیز نادرست است.
گزینه ۳ : در این گزینه h(C)=5, h(B)=1 , h(D)=8 داده شده است و شرط قابل قبول بودن برای این هیوریستیک برقرار است اما همانطور که در گزینه یک اشاره شد این هیوریستیک ناسازگار است پس این گزینه که فقط به قابل قبول بودن این تابع اشاره میکند درست است.
گزینه ۴ : در این گزینه h(C)=3, h(B)=3 , h(D)=8 داده شده است از طرفی میدانیم در صورتی که یک تابع هیوریستیک یکنواخت باشد پس حتما قابل قبول هم هست اما در صورت سوال اشاره شده است که قابل قبول نیست در نتیجه این گزینه نادرست میشود.
نکته : در هیچکدام از گزینه ها به h(A) اشاره نشده است و در این سوال فرض کردیم که هیوریستیک این گره درست و موجب قابل قبول نشدن یا ناسازگاری نمیشود.
دشوار
فرض کنید در سفری به سیبری راه خود را گم کردهاید و بعد از مدتی به یک شهر میرسید. دقیقاً نمیدانید نام این شهر چیست ولی با توجه به محدوده گم شدنتان حدس میزنید این شهر باید یکی از چهار شهر C، B، A یا D باشد. با توجه به اطلاعاتی که در مورد مکان این چهار شهر دارید احتمال حضور در هر یک از چهار شهر $A$، $B$، $C$ و $D$ را به ترتیب 10%، 40%، 10% و 30% میدانید؛ سپس از یکی از اهالی سؤالی میپرسید و او به زبان اسپرانتو پاسخ میدهد. شما میدانید 50% مردم شهر$A$، 20% مردم شهر $B$، 40% مردم شهر $C$ و 30% مردم شهر $D$ به زبان اسپرانتو صحبت میکند. حالا با بیشترین احتمال خود را در کدام شهر میدانید؟
عدم قطعیت
1 B
2 A
3 C
4 D
گزینه 4 صحیح است.
با توجه به صورت سوال در مورد احتمال حضور در هر یک از شهرها داریم:
P(A) = 0.1, P(B) = 0.4, P(C) = 0.1, P(D) = 0.3
از طرفی میدانیم مردم هر شهر با چه احتمالی به زبان اسپرانتو صحبت میکنند و میتوان آن را به صورت زیر نوشت:
P(S|A) = 0.5, P(S|B) = 0.2, P(S|C) = 0.4, P(S|D) = 0.3
صورت سوال گفته است که به شرط صحبت کردن مردم شهر به زبان اسپرانتو احتمال بودن در کدام شهر بیشتر است. برای پاسخ به این سوال ابتدا باید احتمال شرطی بودن در هر شهر به شرط اسپرانتو صحبت کردن را بیابیم و سپس آنها را با هم مقایسه کنیم. برای این کار ابتدا باید احتمال کلی اسپرانتو صحبت کردن را مطابق فرمول زیر بیابیم.
P(S) = P(A)P(S|A) P(B)P(S|B) P(C)P(S|C) P(D)P(S|D) = 0.26
سپس با توجه به قانون بیز داریم :
$P(A|S)\ =\ \frac{P(S|A)P(A)}{P(S)}\ \simeq \ 0.19$
$P(B|S)\ =\ \frac{P(S|B)P(B)}{P(S)}\ \simeq \ 0.3$
$P(C|S)\ =\ \frac{P(S|C)P(C)}{P(S)}\ \simeq \ 0.15$
$P(D|S)\ =\ \frac{P(S|D)P(D)}{P(S)}\ \simeq \ 0.35$
در نهایت با توجه به مقادیر بدست آمده در بالا میبینیم که احتمال بودن در شهر D به شرط اسپرانتو صحبت کردن از همه بیشتر است.
دشوار
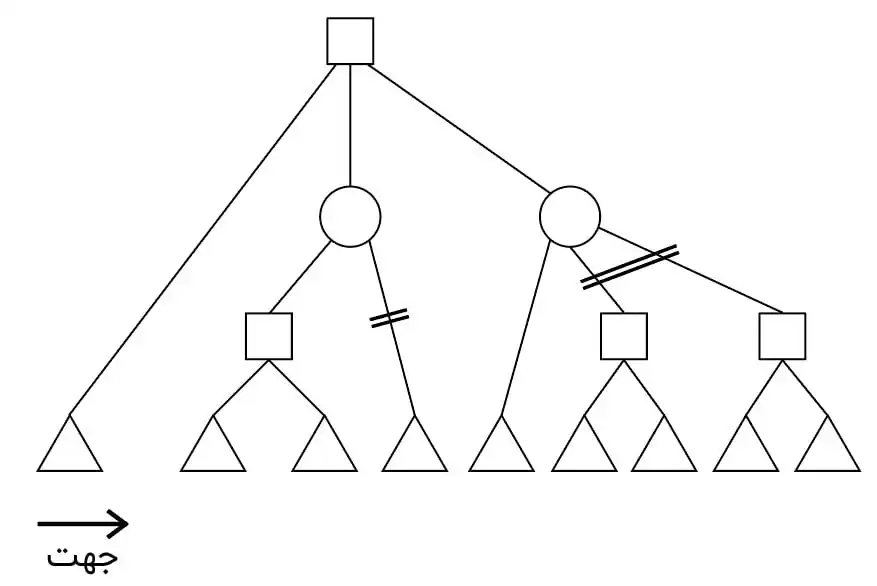
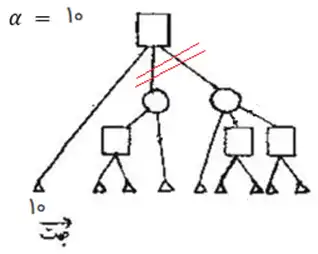
در گراف مقابل مربع نشانه بازیکن Max، دایره نشانه بازیکن Min و مثلث نشانه حالت پایانی است. اگر مقادیر ارزیابی بتوانند در فاصله بسته $\left[\mathrm{\circ }\ ,\mathrm{\ }\mathrm{10}\right]$ باشند و با هرس آلفا- بتا فقط یالهای علامتزده شده با // حذف شوند، ترتیب گرههای پایانی به ترتیب از چپ به راست در شکل کدام یک از گزینههای زیر خواهد بود؟
بازی های رقابتی
1 ${{\mathop{\longrightarrow}\limits_{\ \ \ \ \ \ \ \ \text{جهت}\ \ \ \ \ \ \ }}}$10, 9, 8, 5, 4, 3, 2, 1, 0
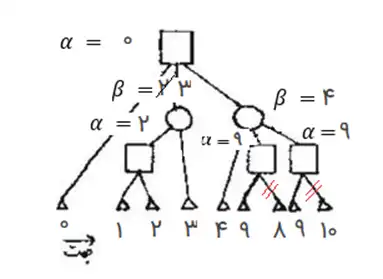
2 ${{\mathop{\longrightarrow}\limits_{\ \ \ \ \ \ \ \ \text{جهت}\ \ \ \ \ \ \ }}}$0, 1, 2, 3, 4, 9, 8, 9, 10
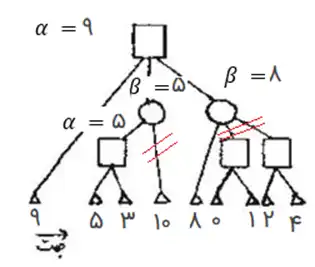
3 ${{\mathop{\longrightarrow}\limits_{\ \ \ \ \ \ \ \ \text{جهت}\ \ \ \ \ \ \ }}}$9, 5, 3, 10, 8, 0, 1, 2, 4
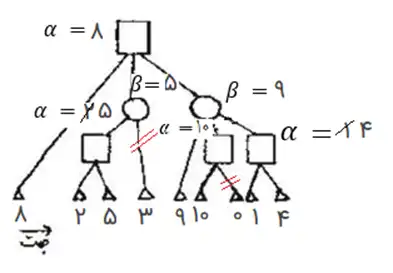
4 ${{\mathop{\longrightarrow}\limits_{\ \ \ \ \ \ \ \ \text{جهت}\ \ \ \ \ \ \ }}}$8, 2, 5, 3, 9, 10, 0, 1, 4
گزینه 3 صحیح است.
در این سوال به بررسی تک تک گزینهها میپردازیم تا ببینیم در کدامیک شرط هرس مطابق شکل داده شده برقرار میشود.
گزینه ۱ : در این گزینه مقدار اولین گره ۱۰ داده شده است که با توجه به اینکه بازه مقادیر را داریم و ۱۰ بیشترین مقدار است، گره ریشه که از نوع max است به بیشترین مقدار رسیده است و شرط هرس برقرار است و سایر گرههای بازدید نشده میتوانند هرس شوند که این حالت معادل شکل داده شده در صورت سوال نیست.
گزینه ۲ : گرههای حذف شده توسط این الگورتیم با مقادیر داده شده در گزینه ۲ نیز به شکل زیر است.
گزینه ۳ : گرههای حذف شده توسط این الگورتیم با مقادیر داده شده در این گزینه به شکل زیر است که همانطور که میبینید مطابق گرههای هرس شده در صورت سوال است.
گزینه ۴ : گرههای حذف شده توسط این الگورتیم با مقادیر داده شده در گزینه ۴ نیز به شکل زیر است.
متوسط
اگر بدانیم
منطق گزارهای
$\mathrm{E\ }\mathrm{\wedge }\mathrm{\ R\ }\mathrm{\Rightarrow }\mathrm{\ B}$
$\mathrm{E\ }\mathrm{\Rightarrow }\mathrm{\ R\ }\mathrm{\vee }\mathrm{\ P\ }\mathrm{\vee }\mathrm{\ L}$
$\mathrm{K\ }\mathrm{\Rightarrow }\mathrm{\ B}$
$\mathrm{\neg }\left(\mathrm{L\ }\mathrm{\wedge }\mathrm{\ B}\right)$
$\mathrm{P\ }\mathrm{\Rightarrow }\mathrm{\ \neg K}$
کدامیک از موارد زیر با استدلال منطقی قابل نتیجهگیری نیست؟
1 $\mathrm{K\ }\mathrm{\wedge }\mathrm{\ E\ }\mathrm{\Rightarrow }\mathrm{\ R}$
2 $\mathrm{E\ }\mathrm{\wedge }\mathrm{\ P}$
3 $\mathrm{L\ }\mathrm{\vee }\mathrm{\ P\ }\mathrm{\Rightarrow }\mathrm{\ \neg K}$
4 $\mathrm{L\ }\mathrm{\Rightarrow }\mathrm{\ \neg }\left(\mathrm{K\ }\mathrm{\wedge }\mathrm{\ E}\right)$
پاسخ گزینه 2 است.
ابتدا گزارهها را به فرم CNF مینویسیم:
1) $\neg E ∨\neg R ∨B$
2) $\neg E ∨R ∨ P ∨ L$
3) $\neg K ∨B$
4) $\neg L ∨ \neg B$
5) $\neg P ∨\neg K$
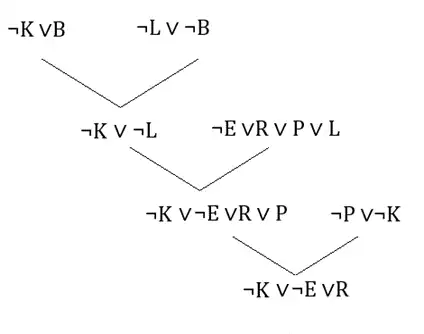
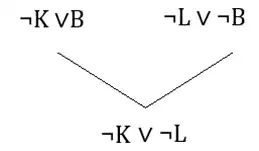
گزینه ۱ : عبارت این گزینه را میتوان به فرم $\neg K ∨ \neg E ∨ R$ نوشت که طبق درخت زیر قابل نتیجهگیری است.
گزینه ۲ : از آنجایی که E از هیچکدام از لیترالها نتیجه گرفته نمیشود و جز حقایق نیز نیست این گزینه از پایگاه دانش قابل نتیجهگیری نیست.
گزینه ۳ : ساده شده عبارت این گزینه به فرم زیر است که بخش اول آن مطابق جمله ۸ پایگاه دانش است و بخش دوم آن از رزولوشن روی جمله ۳ و ۵ بدست میآید(مشابه درخت رسم شده درگزینه ۴). در نتیجه این عبارت قابل نتیجهگیری است.
$(\neg P ∨\neg K) ∧ (\neg L ∨ \neg K)$
گزینه ۴ : عبارت ساده شده این گزینه نیز به فرم $\neg L ∨ \neg K∨\neg E$ میباشد که میتوان طبق درخت زیر بخش اول آن یعنی $(\neg L ∨ \neg K)$ را از پایگاه دانش نتیجه گرفت و از طرفی ∨ این عبارت با ¬E نیز برقرار است پس این گزینه نیز درست است.
تست های درس سیستم های عامل کنکور کامپیوتر ۱۳۹۰ به همراه جواب تشریحی
دشوار
پنج فرآیند $(\ P_\mathrm{4}\ ~ تا~ P_0~)$ ، با مشخصات زمان اجرای نشان داده شده در شکل، به ترتیب $\ P_\mathrm{4}\ ~تا~ P_0$ در صف آماده قرار دارند. هر فرآیند فقط در محلهای مشخص شده در آن، عملیات P(s) یا (wait(s)) و V(s) یا (signal(s)) را بر روی سمافور s با مقدار اولیه یک اجرا میکند. اعداد نوشته شده در کنار آکولادها نشان دهنده طول زمان اجرای آن بخش از فرآیندها میباشند. برای زمانبندی آنها الگوریتم Round Robin) RR) با زمان کوانتوم ۵=q استاده میشود: متوسط زمان بازگشت (turn around) و متوسط زمان انتظار فرآیندهای فوق با زمانبندی مذکور به ترتیب چقدر است؟ توجه شود که فرآیندها براساس FIFO از حالت بلوکه شده (Blocked) خارج میشوند. ضمنأ زمان اجرای P(s) و V(s) را ناچیز در نظر بگیرید.
انحصار متقابل
1 135 , 102
2 133 , 99
3 141 , 108
4 بنبست رخ میدهد و اجرای فرآیندها به اتمام نمیرسد.
گزینه درست وجود ندارد.
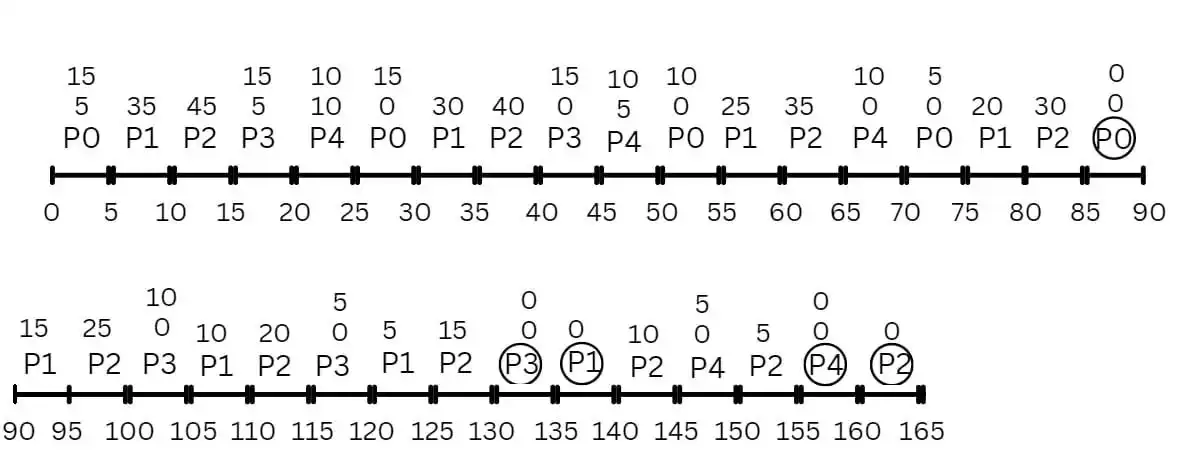
نمودار گانت را برای سیستم رسم میکنیم: (اعداد بالایی زمان باقی مانده هر کد است)
با توجه به نمودار بالا متوسط زمان بازگشت و متوسط زمان انتظار را به صورت زیر بهدست میآوریم:
متوسط زمان بازگشت=$\frac{90+140+165+135+160}{5}=\frac{690}{5}=138$
متوسط زمان سرویس $\mathrm{AST\ =\ }\frac{\left(10+15\right)+40+50+\left(10+15\right)+(15+10)}{5}=\frac{165}{5}=33$
متوسط زمان انتظار $\mathrm{AWT\ =\ ATT}-\mathrm{AST\ =\ }138-33=105$
این سوال سنجش پاسخ صحیح نداشت.
دشوار
اگر در یک سیستم دو فرآیند $P_\mathrm{1}$ و $ \ P_\mathrm{2}$ داشته باشیم که jobهای فرآیند ${\ P}_\mathrm{1}$ و بهصورت دوره ای هر ۵ ثانیه یکبار و jobهای فرآیند ${\ P}_\mathrm{2}$ بهصورت دورهای هر ۴ ثانیه یکبار به سیستم وارد شوند و زمان اجرای هر job از فرآیند $P_\mathrm{1}$ برابر با ۳ ثانیه و زمان اجرای هر job از فرآیند $P_\mathrm{2}$ برابر با ۱ ثانیه باشد، بهرهوری (utilization) و میانگین زمان پاسخ (Average response time) سیستم به ترتیب چه اعدادی خواهند بود؟ الگوریتم زمانبندی RR با برش زمانی ۱=q است و اگر در لحظه t یک job به سیستم وارد شود و در همین لحظه یک job دیگر پردازنده را ترک کرده و به صف آمادگی (ready queue) منتقل شود، اولویت با job قبلی موجود در سیستم است که تازه پردازنده را رها کرده است. زمان پاسخ، تأخیر بین ورود هر job و اولین زمان در اختیار گرفتن پردازنده توسط آن job است.)
فرآیندها و زمانبندی پردازندهها
1 85% , $\frac{\mathrm{5}}{\mathrm{9}}$
2 85% , $\frac{\mathrm{1}}{\mathrm{3}}$
3 90% , $\frac{\mathrm{1}}{\mathrm{3}}$
4 90% , $\frac{\mathrm{5}}{\mathrm{9}}$
با توجه به اینکه سوال در مورد لحظه شروع $(t=0)$ اطلاعاتی نداده است. بنابراین ما فرض را بر این میگذاریم که در لحظه شروع هر دو این jobها وارد سیستم شدهاند و اولویت اجرا را هم به فرآیند $P_1$ اختصاص میدهیم. بنابراین با توجه به توضیحات داده شده نمودار گانت سوال به صورت زیر خواهد بود:
بنابراین بهرهوری CPU برابر است با:
\[\mathrm{Utilization\ =\ }\mathrm{1\ -\ }\frac{\text{زمان}\mathrm{\ }\text{بیکاری}\mathrm{\ }\text{پردازنده}}{\text{زمان}\mathrm{\ }\text{یک}\mathrm{\ }\text{تناوب}}=\frac{17}{20}=85\%\]
و با توجه به تعریف ارائه شده در متن سوال برای زمان پاسخ و همچنین زمانهای پاسخ jobهای دو فرآیند که در زیر آورده شدهاند. میانگین زمان پاسخ سیستم برابر است با:
زمانهای پاسخ برای 4 job وارد شده فرآیند $P_1$ به ترتیب برابر است با: 0,0,0,0
زمانهای پاسخ برای 5 job وارد شده فرآیند $P_2$ به ترتیب برابر است با: 1,0,0,1,1
و میانگین زمان پاسخ سیستم برابر است با: $\frac{1+1+1}{9}=\frac{3}{9}=\frac{1}{3}$
دشوار
حافظه اصلی با وضعیت نشان داده شده در شکل را در نظر بگیرید. اگر مدیریت حافظه اصلی براساس اختصاصدهی پویا باشد و اختصاصدهی فضای خالی به فرآیندها براساس Next-fit انجام گیرد و فرآیندهای ${\ P}_\mathrm{5},....., P_\mathrm{1} ,P_\mathrm{0}$ جهت اجرا شدن، مطابق با اطلاعات جدول زیر وارد سیستم شوند. با فرض اینکه از بین فضاهای پرشماره ۱ تا ۴، فقط فضای پر ۳ در لحظه ۲۰+t آزاد گردد (دیگر فضاهای پر تا اتمام اجرای فرآیندهای فوق آزاد نمیگردند)، متوسط زمان بازگشت (turn around) و متوسط زمان انتظار فرآیندهای فوق در روش FCFS به ترتیب چقدر است؟
مدیریت حافظه
| فضای پر ۱ (۳۰ KB) |
| فضای خالی ۱ (20 KB) |
| فضای پر ۲ (10 KB) |
| فضای خالی ۲ (40 KB) |
| فضای پر ۳ (20 KB) |
| فضای خالی ۳ (۳۰ KB) |
| فضای پر ۴ (40 KB) |
| فضای خالی ۴ (۳۰ KB) |
| زمان سرویس |
حافظه مورد نیاز (KB) |
زمان ورود |
فرآیند |
| 30 |
25 |
$t$ |
$p_0$ |
| 40 |
20 |
$t +1$ |
$p_1$ |
| 20 |
40 |
$t +2$ |
$p_2$ |
| 45 |
25 |
$t +3$ |
$p_3$ |
| 35 |
10 |
$t +4$ |
$p_4$ |
| 15 |
35 |
$t +5$ |
$p_5$ |
1 109/5 , 85/83
2 109/5 , 78/67
3 110/83 , 80
4 116/67 , 85/83
با توجه به فرض سوال مدیریت حافظه اصلی براساس اختصاصدهی پویا و براساس الگوریتم Next Fit انجام میشود. با توجه به این فرض تخصیص فضایهای خالی براساس زمان در جدول زیر آورده شده:
E
(30KB) |
F
(40KB) |
E
(30KB) |
E
(30KB) |
E
(40KB) |
F
(10KB) |
E
(20KB)
|
F
(30KB)
|
T= 0 |
E
(30KB) |
F
(40KB) |
E
(30KB) |
F
(20KB) |
E(15) |
F(25) |
F
(10KB) |
E
(20KB)
|
F
(30KB)
|
T= t |
E
(30KB) |
F
(40KB) |
E(10) |
F(20)
$p_1$ |
F
(20KB) |
E(15) |
F(25) |
F
(10KB) |
E
(20KB) |
F
(30KB)
|
T= t+1 |
E
(30KB) |
F
(40KB) |
E(10) |
F(20)
$p_1$ |
F
(20KB) |
E(15) |
F(25) |
F
(10KB) |
E
(20KB) |
F
(30 KB)
|
T= t+2 |
| E(5) |
F(250)
$p_3$ |
F
(40KB) |
E(10) |
F(20)
$p_1$ |
F
(20KB) |
E(15) |
F(25) |
F
(10KB) |
E
(20KB) |
F
(30 KB)
|
T= t+3 |
| E(5) |
F(250)
$p_3$ |
F
(40KB) |
E(10) |
F(20)
$p_1$ |
F
(20KB) |
E(15) |
F(25) |
F
(10KB) |
E(10) |
E(10)
$p_4$
|
F
(30KB)
|
T= t+4 |
| E(5) |
F(250)
$p_3$ |
F
(40KB) |
E(10) |
F(20)
$p_1$ |
F
(20KB) |
E(15) |
F(25) |
F
(10KB) |
E(10) |
E(10)
$p_4$
|
F
(30KB)
|
T= t+5 |
| E(5) |
F(250)
$p_3$ |
F
(40KB) |
E(10) |
F(20)
$p_1$ |
E(35) |
F(25) |
F
(10KB) |
E(10) |
E(10)
$p_4$
|
F
(30KB)
|
T= t+20 |
| E(5) |
F(250)
$p_3$ |
F
(40KB) |
E(10) |
F(20)
$p_1$ |
E(35) |
F(35) |
F
(10KB) |
E(10) |
E(10)
$p_4$ |
F
(30KB)
|
T= t+20 |
| E(30) |
F
(40KB) |
E(30) |
(E(20 |
F(40)
$p_2$ |
F
(10KB) |
E(20)
|
F
(30KB)
|
T= t+165 |
با توجه نمودار تخصیص فوق و الگوریتم زمانبندی بیان شده در سوال (FCFS) نمودار گانت سیستم به صورت زیر خواهد بود:
با توجه به نمودار گانت فوق متوسط زمان انتظار و متوسط زمان بازگشت به صورت زیر به دست میآید: (t=0 فرض شد)
متوسط زمان انتظار=$\frac{\left(30-0-30\right)+\left(70-1-40\right)+\left(115-3-45\right)+\left(150-4-35\right)+\left(165-5-15\right)+\left(185-2-20\right)}{6}=\frac{515}{6}=85.83$
متوسط زمان بازگشت=$\frac{\left(30-0\right)+\left(70-1\right)+\left(115-3\right)+\left(150-4\right)+\left(165-5\right)+\left(185-2\right)}{6}=\frac{700}{6}=116.67$
متوسط
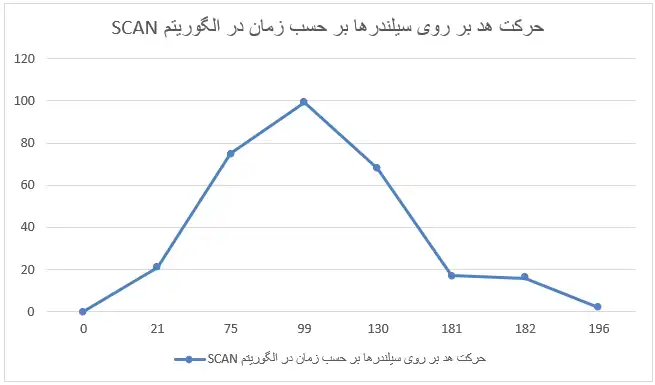
یک دیسک را در نظر بگیرید که شامل ۱۰۰ سیلندر است (۰ تا ۹۹). زمان لازم برای عبور هد از یک سیلندر به سیلندر مجاور یک واحد زمانی است. در زمان صفر هد بر روی سیلندر صفر است و درخواستی از گذشته وجود ندارد. شش درخواست در زمانهای مختلف مطابق جدول زیر وارد میشوند.
مدیریت I/O و دیسک
زمان ورود درخواست: ۰ ۱۰ ۲۰ ۷۰ ۸۰ ۹۰
سیلندر درخواست شده: ۲۱ ۷۵ ۱۶ ۶۸ 2 17
در زمان حرکت هد به سمت یک سیلندر، ورود درخواست جدید تأثیری بر حرکت ندارد. ترتیب اجرای درخواستها برای الگوریتم SCAN (یا آسانسور) چیست؟
1 0 21 75 16 17 2 68
2 0 21 75 16 2 17 68
3 0 21 75 16 68 2 17
4 0 21 75 68 16 2 17
مسیر حرکت هد با توجه به الگوریتم SCAN و درخواستها به صورت شکل زیر خواهد بود:
که با توجه به این نمودار ترتیب اجرای درخواستها برابر است با: $2\gets16\gets17\gets68\gets75\gets21\gets0$ اما این ترتیب در گزینهها وجود ندارد.
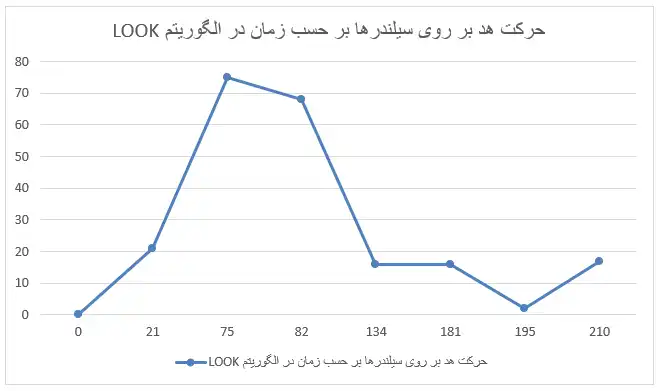
با دقت در متن سوال متوجه خواهیم شد که طراح بعد از بیان واژه SCAN در داخل پرانتز معادل فارسی آن را آسانسور بیان کرده است، این در حالی است که آسانسور معادل فارسی الگوریتم LOOK است.
حال اگر سوال را برای الگوریتم LOOK حل کنیم جواب درست بدست خواهد آمد.
که با توجه به این نمودار ترتیب اجرای درخواستها برابر است با: $17\gets2\gets16\gets68\gets75\gets21\gets0$
متوسط
در این سوال تفاوتهای مابین تغییر متن (context switch) در فرآیندها و تغییر متن در نخهای یک فرآیند بررسی میشوند، کدام گزینه صحیح است؟
فرآیندها و زمانبندی پردازندهها
1 تغییر متن در فرآیندها موجب تغییر اشارهگر پشته (SP) و پاک شدن TLB میشود.
تغییر متن در نخها موجب تخصیص سهم زمانی تازه میشود و برنامه شمار (PC) تغییر مییابد.
2 تغییر متن در فرآیندها موجب تغییر ثباتهای اجرایی برنامه میشود و با TLB کاری ندارد.
تغییر متن در نخها موجب تغییر اشارهگر پشته (SP) و پاک شدن TLB میشود.
3 تغییر متن در فرآیندها موجب تغییر ثباتهای اجرایی برنامه میشود و سیاستهای حفاظتی را تغییر میدهد.
تغییر متن در نخها موجب تغییر اشارهگر پشته (SP) و پاک شدن TLB میشود.
4 تغییر متن در فرآیندها موجب تغییر ثباتها اجرایی برنامه و تغییر برنامه شماره (PC) میشود.
تغییر متن در نخها ثبات و جداول مدیریت حافظه را تغییر نمیدهد و اشارهگر پشته (SP) را تغییر میدهد.
بررسی گزینهها:
گزینه 1: بخش اول این گزاره درست است اما در بخش دوم، فرآیند تغییر متن در نخها همواره باعث تخصیص سهم زمانی جدید نمیگردد. بنابراین این گزینه نادرست است.
گزینه 2: بخش اول این گزاره نادرست است زیرا فرآیند تغییر متن در فرآیندها، TLB را دستخوش تغییراتی میکند. بخش دوم این گزاره نیز همانند بخش اول نادرست است زیرا فرآیند تغییر متن در نخها سبب پاک شدن TLB نمیشود. بنابراین این گزاره تماما نادرست است.
گزینه 3: بخش دوم این گزاره نادرست است و فرآیند تغییر متن در نخها باعث پاک شدن TLB نمیگردد. بنابراین این گزینه نادرست است.
گزینه 4: موارد ذکر شده در هر دو بخش گزینه 4 درست هستند. بنابراین این گزاره درست است.
متوسط
آیا میتوان یک مانیتور را از داخل یک مانیتور دیگر فراخوانی کرد؟
انحصار متقابل
1 امکانپذیر است ولی نتیجه غلط خواهد داد.
2 امکانپذیر است و مشکلی ندارد.
3 امکانپذیر است ولی میتواند به بنبست بیانجامد.
4 امکانپذیر است به شرطی که زنجیرهوار ادامه نیابد و فقط شامل دو مانیتور باشد.
از نظر ساختاری و طراحی مانیتورها امکان فراخوانی یک مانیتور از درون یک مانیتور دیگر وجود دارد. اما امکان وجود بنبست نیز وجود دارد. به مثال زیر توجه کنید: فرض میکنیم فرایند $p_1$ وارد مانیتور A شود و فرایند $p_2$ وارد مانیتور B. با این فرض اگر فرایند $p_1$ قصد ورود به مانیتور B را داشته باشد، به علت اینکه فرایند دیگری مانیتور B را اشغال کرده است، $p_1$ مسدود میشود و به حالت خواب میرود. سپس اگر فرایند $p_2$ قصد ورود به مانیتور A را داشته باشد چون مانیتور A اشغال است، $p_2$ نیز مسدود شده و سیستم به بن بست میخورد.
تست های درس الکترونیک دیجیتال کنکور کامپیوتر ۱۳۹۰ به همراه جواب تشریحی
آسان
دیاگرام میلهای (Stick Diagram) زیر نمایانگر مدار کدامیک از توابع زیر است؟
خانواده پویای MOSFETها
1 $Y=\overline{B+CD}$ (مدار پویا)
2 $Y=\overline{B}\cdot\overline{C}\cdot\overline{D}$ (مدار پویا)
3 $y=\overline{A+B+C\cdot D}$ (مدار ایستا)
4 $Y=\overline{A}+\overline{B}\cdot\overline{C}\cdot\overline{D}$ (مدار ایستا)
مدار PD به صورت زیر است:
بنابراین گزینه 1 صحیح است.
آسان
با فرض آن که مقدار ولتاژ آستانه برای ترانزیستور pMOS برابر -0.4 V باشد، کدام گزینه وضعیت صحیح بایاس را برای هر سه حالت (الف)، (ب) و (ج) درست نشان داده است؟
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
1 (الف) = (ب) = خطی و (ج) = اشباع
2 (الف) = اشباع، (ب) = خطی و (ج) = نقطه مرزی اشباع و خطی
3 (الف) = (ج) = اشباع و (ب) = خطی
4 (الف) = اشباع، (ب) = قطع و (ج) = نقطه مرزی اشباع و خطی
گزینه 2 صحیح است.
ترانزیستور PMOS روشن است اگر:
$V_{SG}>\left|V_{tp}\right|=0.4$
اگر ترانزیستور PMOS روشن باشد شرط خطی و اشباع بودن آن به شرح زیر است:
$V_{SD}<V_{SG}-\left|V_{tp}\right|\to Triod$
$V_{SD}>V_{SG}-\left|V_{tp}\right|\to Saturated$
سر Source ترانزیستور آن سری است که ولتاژ بیشتری دارد.
مدار الف) اشباع
$V_{SG}=2.2-0.8=1.4V,\ V_{SD}=2.2V$
$\to V_{SG}>0.4,\ 2.2=V_{SD}>V_{SG}-\left|V_{tp}\right|=1.4-0.4=1\to Saturated$
مدار ب) خطی
$V_{SG}=3.5-0.5=3V,\ V_{SD}=3.5-2.3=1.2V$
$\to V_{SG}>0.4,\ 1.2=V_{SD}<V_{SG}-\left|V_{tp}\right|=3-0.4=2.6\to Triod$
مدار ج) نقطه مرزی اشباع و خطی
$V_{SG}=1.1+0.4=1.5V,\ V_{SD}=1.1V$
$\to V_{SG}>0.4,\ 1.1=V_{SD}=V_{SG}-\left|V_{tp}\right|=1.5-0.4=1.1\to Saturated\ or\ Triod$
آسان
فرض کنید مقادیر مندرج در جدول زیر توسط طراح سختافزار برای یک ترانزیستور MOS اندازهگیری شده باشند.
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
| $I_D(\mu A)$ |
$V_{BS}$ |
$V_{DS}$ |
$V_{GS}$ |
$\begin{cases} I_D(Sat)=\frac {K}{2}(V_{GS}-V_{TH})^2(1+\lambda V_{DS}) \\ I_D(Linear)=\frac {K}{2}[2(V_{GS}-V_{TH}) V_{DS}-V^2_{DS} ] \end{cases}$ |
| 10 |
0 |
5 |
2 |
| 400 |
0 |
5 |
5 |
| 280 |
-3 |
5 |
5 |
| 480 |
0 |
8 |
5 |
پارامتر ضریب مدولاسیون این وسیله چیست؟
1 $0.1\ V^{-1}$
2 $0.03\ V^{-1}$
3 $0.02\ V^{-1}$
4 $0.05\ V^{-1}$
گزینه 1 صحیح است.
منظور از ضریب مدولاسیون $\lambda$ میباشد. با توجه به فرمولها برای یافتن $\lambda$ باید ردیفهایی را انتخاب کنیم که ترانزیستور در حالت اشباع است.
اشباع زمانی رخ میدهد که :
$V_{DS}>V_{GS}-V_{TH}$
چون $V_{TH} \gt 0$ است تمام ردیفهای آورده شده در جدول اشباع میباشند.
از ردیف سوم نباید استفاده شود زیرا در آن ولتاژ بدنه صفر نبوده و ما فرمول محاسبه آن را نداریم.
با توجه به فرمول جریان اشباع میتوان به راحتی با استفاده از دو ردیف دوم و چهارم ضریب مدولاسیون را یافت. علت آن مساوی بودن $V_{GS}$ در این دو ردیف است.
$\left\{ \begin{array}{c} \frac{K}{2}\left(5-V_{TH}\right)\left(1+5\lambda \right)=400 \\ \frac{K}{2}\left(5-V_{TH}\right)\left(1+8\lambda \right)=480 \end{array} \right.$
با تقسیم دو رابطه داریم:
$\frac{1+5\lambda }{1+8\lambda }=\frac{400}{480}\to 80=800\lambda \to \lambda =0.1(V^{-1})$
متوسط
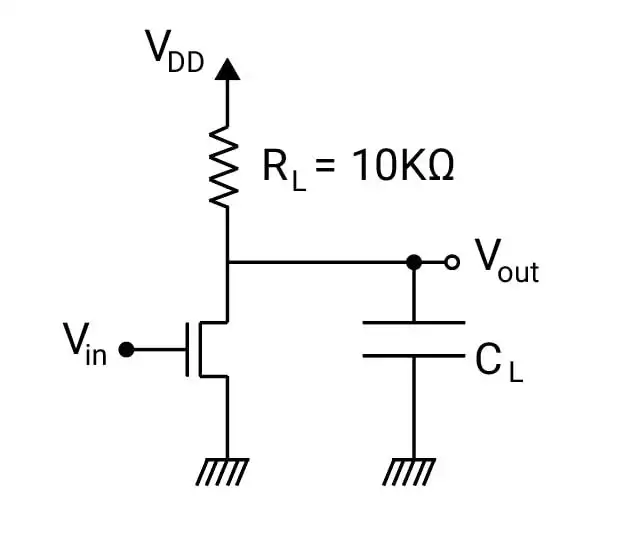
برای یک معکوسکننده با بار مقاومتی با روش جریان متوسط $\left(t_p=\frac{C_{load}*\Delta V}{I_{\text{متوسط}}}\right)$ زمان گذر $t_{PHL}$ چند نانوثانیه (ns) است؟ ورودی تابع پله ایدهآل با گذر از صفر به $V_{DD}$ در زمان صفر است.
محاسبه تاخیر
$V_{DD}=5V\ ,\ \mu_n C_{OX}=25\frac{\mu A}{V^2}\ ,\ R_L=10k\ ,\ \left(\frac{W}{L}\right)_n=10\ ,\ C_L=1pF(\text{پیکوفاراد})\ ,\ V_{tn}=1V$
1 $1.13$
2 $1.26$
3 $2.1$
4 $1.85$
گزینه 2 صحیح است.
آسان
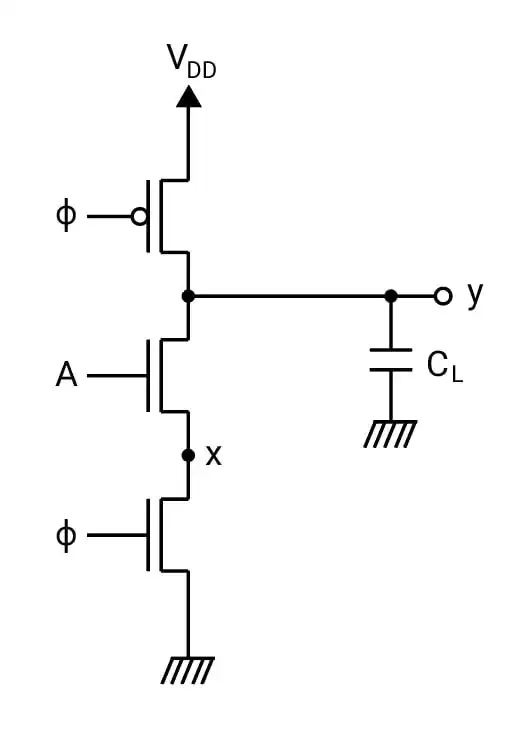
در مدار دینامیکی زیر ابتدا سیگنال $\phi$ صفر است و سپس مقدار آن یک میشود. فرض کنید مدت طولانی در مقدار صفر سپری شده است. مقدار سیگنال A هم یک است. در ابتدای زمان یک شدن سیگنال $\phi$ ، ولتاژ در گره میانی (x) چند ولت (V) است؟
خانواده پویای MOSFETها
$C_L=200fF(\text{فمتوفاراد})\ ,\ \mu_n C_{OX}= 200 \frac{\mu A}{V^2},\mu_p C_{OX} $$= 60 \frac{\mu A}{V^2} ,\ \gamma=0\ ,\ \lambda=0 $
$|V_t|=0.5V\ ,\ V_{DD}=2V=$ سطح ورودی یک , $ (\frac{W}{L})_p=5\ ,\ (\frac{W}{L})_n=4 $ برای همه nMOS ها
1 0
2 1.5
3 1
4 2
گزینه 2 صحیح است.
نکته: در حل این سؤال به این نکته توجه کنید که PMOS ولتاژ بالا را کامل عبور میدهد در حالیکه NMOS از ولتاژ بالا به مقدار $V_t$ کم میکند. (این نکته زمانی درست است که جریان عبور صفر باشد و یا نهایت صفر شود.)
در زمان صفر بودن $ϕ$ خازن کامل شارژ شده در نتیجه جریان عبور PMOS صفر شده و براساس نکته بالا ولتاژ خازن برابر $V_{DD}=2$ میشود.
در لحظه یک شدن $ϕ$ ترانزیستور A جریانی عبور نمیدهد در نتیجه با توجه به نکته بالا چون ولتاژ یک سر دیگر آن 2 است ولتاژ نقطه x برابر است با: $V_x=2-V_t=2-0.5=1.5$
متوسط
در گیت شبهانموس (Pseudo nMOS) زیر بدترین مقدار $V_{OL}$ چند ولت (V) است؟ فرض کنید:
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
$(\frac{W}{L})_p=2\ ,\ (\frac{W}{L})_n=8\ ,\ \mu_nC_{OX}=200\frac{\mu A}{V^2}\ ,\ \mu_p C_{OX}=60\frac{\mu A}{V^2}\ ,\ \gamma=0\ ,\ \lambda=0 \\ |V_t|=0.5V\ ,\ V_{DD}=2V$
1 0.057
2 0.234
3 0.1
4 0.245
گزینه 4 صحیح است.
بیشترین ولتاژ خروجی در زمان صفر منطقی خروجی زمانی اتفاق میافتد که NMOSها بیشترین مقاومت را داشته باشند.
بیشترین مقاومت زمانی رخ میدهد که در مسیری با بیشترین تعداد NMOS از خروجی به صفر است تمام NMOSهای آن مسیر روشن باشند و دیگر NMOSها خاموش (هر NMOS را یک مقاومت در نظر بگیرید.).
با توجه به شکل چنین مسیری دارای ۴ NMOS است. میتوان این ۴ NMOS را با یک NMOS با طول $\frac{W}{L}=\frac{1}{4}\left(\frac{W}{L}\right)_n$ تقریب زد. این مقدار با توجه به نکته زیر بدست آمد:
نکته: W/Lها در ترانزیستورهای موازی به صورت مستقیم جمع میشوند و در ترانزیستورهای سری حاصل نهایی برابر معکوس جمع معکوس شده W/Lهاست. (برعکس مقاومتها، مشابه خازنها) (W/L هر ترانزیستور را با T نمایش میدهیم)
$\frac{1}{T_{total}}=\frac{1}{T}+\frac{1}{T}+\frac{1}{T}+\frac{1}{T}=\frac{4}{T}\to T_{total}=\frac{1}{4}\times T=\frac{1}{4}\times \frac{W}{L}$
در مدار نهایی یک PMOS در بالا و یک NMOS در پایین داریم.
فرض میکنیم NMOS در حالت خطی است و PMOS در حالت اشباع (با توجه به گزینهها این فرض درست در میآید.)
$V_{GSn}=V_{dd}=2V,\ V_{DSn}=V_o,\ V_{SGp}=V_{dd}=2V$
$I_{DSn}=I_{DSp}$
$\to {\mu }_nC_{ox}\frac{1}{4}{\left(\frac{W}{L}\right)}_n\left(V_{DS}\left(V_{GS}-V_{tn}\right)-\frac{V^2_{DS}}{2}\right)=\frac{1}{2}{\mu }_pC_{ox}{\left(\frac{W}{L}\right)}_p{\left(V_{SG}-\left|V_{tp}\right|\right)}^2$
$\to 200\times \frac{1}{4}\times 8\left(V_o\left(2-0.5\right)-\frac{V^2_o}{2}\right)=\frac{1}{2}\times 60\times 2{\left(2-0.5\right)}^2$
$\to 800\left(1.5x-\frac{V^2_o}{2}\right)=270\to -40V^2_o+120V_o-27=0\to V_o=\left\{ \begin{array}{c} 0.245 \\ 2.75\ غ\ ق\ ق \end{array} \right.$
آسان
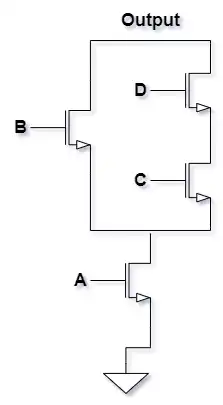
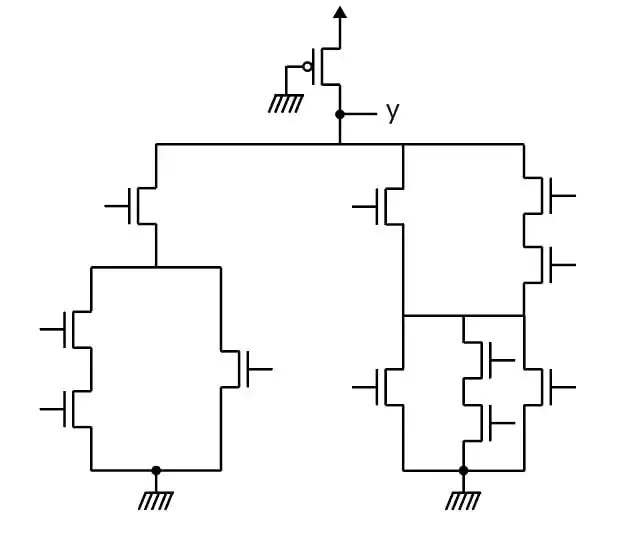
یک فروشگاه دارای یک باجه فروش سریع و سه باجه فروش عادی است. گیشه فروش سریع فقط وقتی راهاندازی میشود که دو یا بیشتر از گیشههای فروش عادی مشغول باشند. فرض کنید متغیرهای بولی (Boolean) C ,B ,A وضعیت هر یک از گیشههای فروش عادی را نشان دهد (1 مشغول و صفر بیکار) کدام یک از مدارهای زیر در سرعت مشابه کمترین مساحت را برای طراحی در مناطق CMOS استاندارد دارا میباشد؟ خروجی out مدیر فروشگاه را از ضرورت راهاندازی باجه فروش سریع آگاه میسازد.
مدارهای ترکیبی
1 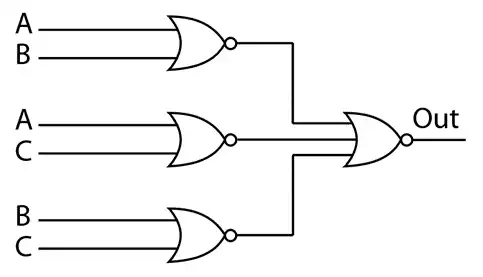
2 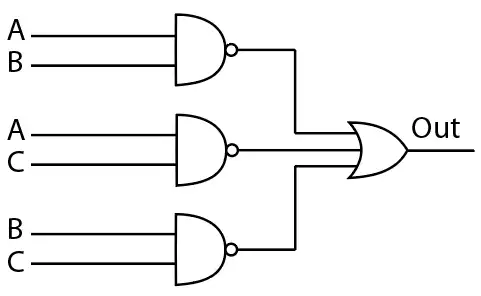
3 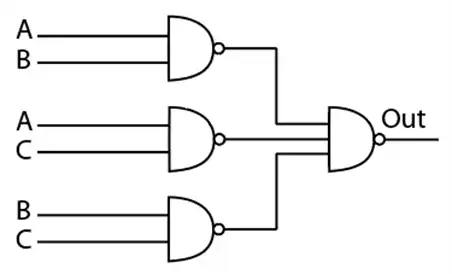
4 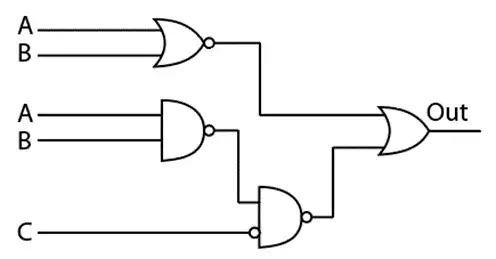
برای حل این مسأله، ابتدا باید تابع منطقی مورد نظر برای راهاندازی باجه فروش سریع را بیابیم.
باجه فروش سریع باید فقط زمانی راهاندازی شود که دو یا بیشتر از گیشههای فروش عادی مشغول باشند. بنابراین باید تابع منطقیای داشته باشیم که زمانی خروجی 1 بدهد که حداقل دو تا از متغیرهای A، B و C برابر 1 باشند.
تابع منطقی برای تشخیص این حالتها به صورت زیر است:
$\text{Out} = (A \cdot B) + (B \cdot C) + (A \cdot C)$
این تابع خروجی را زمانی 1 میکند که حداقل دو تا از گیشهها مشغول باشند.
گزینه 1
- طراحی بر اساس NORها میتواند تابع بالا را ایجاد کند، ولی این روش برای پیادهسازی ممکن است به تعداد بیشتری ترانزیستور نیاز داشته باشد.
گزینه 2
- این روش نیز به پیادهسازی تابع بالا میپردازد ولی نیاز به OR gate دارد که با NAND ها ترکیب شده باشد.
گزینه 3
- این گزینه بهینهترین راهحل است زیرا تابع حاصل میتواند با حداقل تعداد ترانزیستورها پیادهسازی شود و نیاز به یک NOR یا OR اضافی ندارد.
گزینه 4
- مدار خروجی شکل داده شده یک تابع خاص از A، B و C را پیادهسازی میکند که نسبت به گزینههای دیگر پیچیدهتر است و نیازمند تعداد بیشتری گیت است. در نتیجه، این مدار نسبت به گزینههای دیگر مساحت بیشتری را در فناوری CMOS استاندارد نیاز دارد و پیادهسازی بهینهای نخواهد داشت.
نتیجهگیری: کمترین مساحت در طراحی CMOS استاندارد مربوط به گزینه 3 است. این گزینه هم از نظر سرعت و هم از نظر تعداد ترانزیستورها بهینهترین است.
آسان
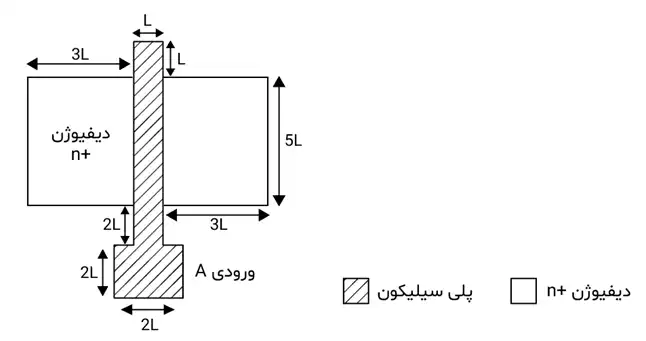
در جانمایی داده شده، خازن ملاحظه شونده از ورودی A چند $fF$ (فمتوفاراد) است؟
محاسبه تاخیر
(فمتوفاراد برمیکرومتر مربع) $\mathrm{\ }C_{poly-over-field}=0.2\frac{fF}{\mu m^2}$پلی روی اکسید میدان
(فمتوفاراد برمیکرومتر مربع) $C_{poly-over-channel}=2\frac{fF}{\mu m^2}$ پلی روی کانال، $L=1\mu m$
1 $2.4$
2 $15$
3 $11.4$
4 $24$
یک پلی از روی دیفیوژن رد شده است، پس یک ترانزیستور NMOS داریم. از تقاطع پلی و دیفیوژن گیت بدست میآید. این شکل نمای بالای ترانزیستور را نشان میدهد و سمت چپ و راست پلی سورس و درین قرار دارد.
ظرفیت خازن پلی یا فلز برابر مجموع خازن مساحت و خازن محیط است. در این سوال از خازن محیط صرف نظر شده است:
$C_{poly} = 5 \times 1 \times 2 + \left(1 \times 1 + 2 \times 1 + 2 \times 2\right) \times 0.2 = 10 + 1.4 = 11.4 \, \text{fF}$
بنابراین گزینه 3 صحیح است.
آسان
نمودار زیر نمای مقطعی از یک گیت منطقی با دو ورودی A و B را به تصویر کشیده شده است. تابع منطقی Y چیست؟
تکنولوژی ساخت مدارهای دیجیتال
1 $Y=AND(A,\ B)$
2 $Y=XOR(A,\ B)$
3 $Y=NOR(A,\ B)$
4 $Y=NAND(A,\ B)$
مدار PD به صورت زیر است:
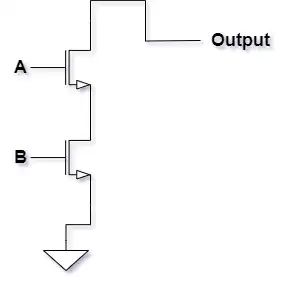
بنابراین
گزینه 4 صحیح است.
آسان
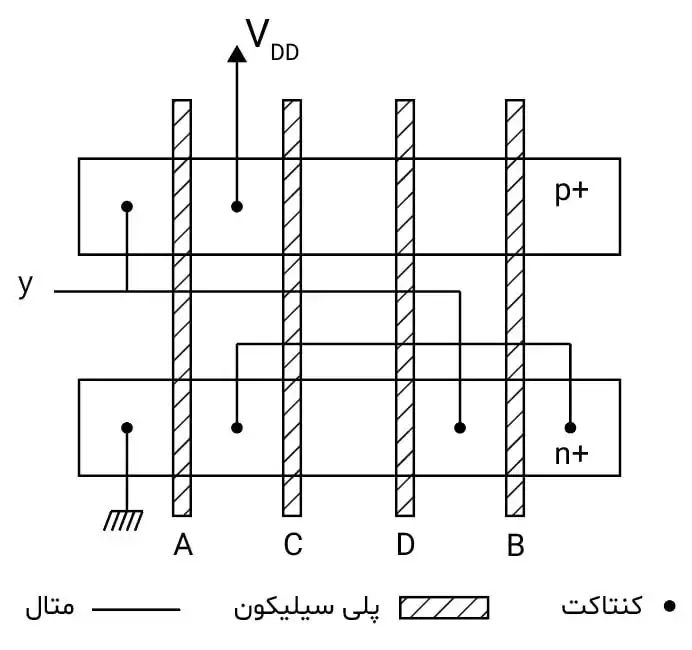
در مدار پایینبر نشان داده شده در شکل و مدار بالابر متناظر آن در تحقق سی موس میخواهیم یک جانمایی (لی آوت) داشته باشیم که قطعات یکپارچهای از مناطق دیفیوژن $n^+$ و $p^+$ بدون بریدگی آن را پیادهسازی نمایند و هر ورودی به یک قطعه پلی سیلیکون متصل شود که این مناطق دیفیوژن را به صورت عمودی قطع نماید. چه ترتیبی از ورودیها برای این کار مناسب است؟
تکنولوژی ساخت مدارهای دیجیتال
1 ABCDEFGH
2 FABEHGDC
3 CEGFABDH
4 ترتیب مناسبی برای این کار وجود ندارد.
باید شرایط و ساختار مدار CMOS را به دقت بررسی کنیم. هدف این است که دیفیوژنهای $n^+$ و $p^+$ بدون بریدگی و به صورت یکپارچه ایجاد شوند و هر ورودی به یک قطعه پلیسیلیکون متصل شود که این مناطق دیفیوژن را به صورت عمودی قطع کند.
تحلیل مدار
1. مدار پایینبر (NMOS): ترانزیستورهای NMOS که به صورت سری متصل هستند، باید به گونهای مرتب شوند که دیفیوژن $n^+$ آنها به صورت یکپارچه و بدون بریدگی شکل بگیرد.
2. مدار بالابر (PMOS): مشابه مدار پایینبر، ترانزیستورهای PMOS نیز باید به گونهای مرتب شوند که دیفیوژن $p^+$ آنها به صورت یکپارچه شکل بگیرد.
با در نظر گرفتن چینش ترانزیستورها در این مدار و شرایط مطرحشده:
- چیدمان ورودیها: به گونهای که ورودیها به یک قطعه پلیسیلیکون متصل شوند و این قطعات دیفیوژن را به صورت عمودی قطع کنند.
- یکپارچگی دیفیوژنها: باید طوری باشد که هیچ بریدگی در مناطق دیفیوژن $n^+$ و $p^+$ وجود نداشته باشد.
وقتی تلاش میکنیم ورودیها را با توجه به شرایط دادهشده مرتب کنیم، متوجه میشویم که هیچ ترتیبی از ورودیها نمیتواند همزمان تمامی شرایط مورد نظر را برآورده کند. به عبارت دیگر:
- اگر بخواهیم دیفیوژنهای $n^+$ و $p^+$ را بدون بریدگی حفظ کنیم، برخی از ورودیها به درستی به قطعات پلیسیلیکون متصل نمیشوند.
- اگر ورودیها را به گونهای مرتب کنیم که تمامی آنها به درستی متصل شوند، دیفیوژنها به صورت یکپارچه باقی نمیمانند.
نتیجه: هیچ ترتیبی از ورودیها نمیتواند شرایط مطرحشده را به طور کامل برآورده کند. به همین دلیل، گزینه 4 که میگوید "ترتیب مناسبی برای این کار وجود ندارد" صحیح است.
تست های درس نظریه زبان ها و ماشین ها کنکور کامپیوتر ۱۳۹۰ به همراه جواب تشریحی
متوسط
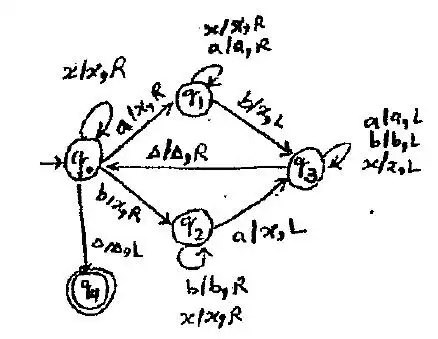
ماشین تورینگ مقابل چه زبانی را میپذیرد؟ $\Delta$ نماد خنثی ماشین تورینگ است و مقصود از $n_a(W)$ تعداد aهای موجود در w است.
ماشینهای تورینگ
1 $\left \{w\in(a+b)^\ast:w=w^R\right \}$
2 $\left \{a^nb^n: n \ge \circ \right \}$
3 $\left \{w\in(a+b+x)^\ast:n_a(w)=n_b(w) \right \}$
4 $\left \{ax:x\in (a+b)^\ast \right \}\cup \left \{bx:x\in(a+b)^\ast \right \}$
برای فهم این موضوع باید رشتههای متعلق به هر گزینه را در ماشین داده شده بررسی کنیم. اما نکته جالب در این سوال این است که در ماشین داده شده میتوان حرف x را از ورودی خواند و این یعنی حرف x باید به الفبای زبان تعلق داشته باشد که این امر تنها در گزینه 3 رعایت شده است.
متوسط
ماشین متناهی $M$ مفروض است. کدام عبارت منظم معادل $L(M)$ است؟
زبان و گرامرهای منظم
1 ${(\mathbf{0}|\mathbf{1})(\mathbf{0}|\mathbf{010}|\mathbf{011})}^\ast$
2 $(\mathbf{0}|\mathbf{1}){(\mathbf{011}|\mathbf{010})}^\ast$
3 $(\mathbf{1}|\mathbf{0}){(\mathbf{011}|\mathbf{11}|\mathbf{10}|\mathbf{0})}^\ast$
4 ${\left(\mathbf{0}\left(\mathbf{011}\right)^\ast\left|\mathbf{1}\left(\mathbf{011}\right)^\ast\right|\mathbf{0}\left(\mathbf{10}\right)^\ast\middle|\mathbf{0}\left(\mathbf{011}\right)^\ast\right)}^\ast$
ماشین داده شده یک DFA است. حال باید بررسی کنیم که کدام رشتهها توسط ماشین پذیرفته میشود اما در گزینهها وجود ندارد (و برعکس) تا آن گزینه را رد کنیم. حالت اولیه ماشین به صورت پذیرش نیست در نتیجه رشته لاندا به زبان این ماشین تعلق ندارد (حذف گزینه 4). با کمی دقت به گزینههای اول دوم میتوان فهمید که پرانتز دوم هر کدام از این عبارتها با حرف 0 شروع میشود که اگر یکی از حروف اول پرانتز اول را هم در نظر بگیریم میتوان گفت که گزینههای اول و دوم رشتههایی با شرایط خاص را تولید میکنند که حرف دوم آنها 0 است. حال اگر بتوان رشتهای یافت که حرف دوم آن غیر 0 (یک) باشد و توسط ماشین پذیرفته شود آنگاه متوجه میشویم که این دو گزینه غلط هستند. رشتهی 111 توسط ماشین پذیرفته میشود اما به زبان گزینههای 1 و 2 تعلق ندارد (حذف گزینه 1 و 2).
متوسط
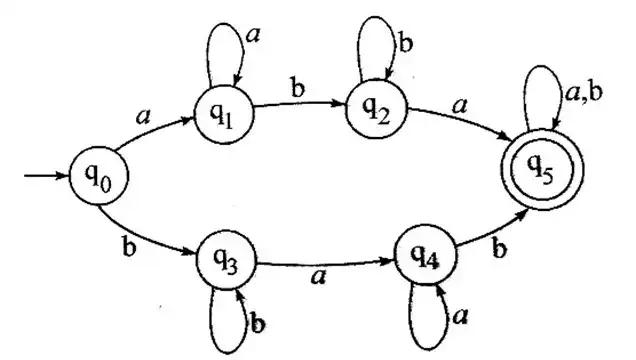
ماشین مقابل چه زبانی را معرفی میکند؟
زبان و گرامرهای منظم
1 تمام رشتههایی که هم شامل زیر رشتهی ab و هم زیر رشتهی ba هستند.
2 رشتههایی به صورت ${({a}+{b})}^\ast{({abba}+{baab})({a}+{b})}^\ast$
3 رشتههایی که با a شروع میشوند و تناوبی ab دارند یا رشتههایی که با b شروع میشوند و تناوبی ba دارند.
4 رشتههایی که به صورت $\bar{w}$, ${{\bar{{w}}({a}+{b})}^\ast+{w}({a}+{b})}^\ast$ همان $w$ است که هر a با b و هر b با a جایگزین شده است.
بررسی گزینه 2: رشتهی aba توسط ماشین پذیرفته میشود اما توسط عبارت منظم داده شده در این گزینه قادر به تولید نیست (حذف گزینه 2).
بررسی گزینه 3: رشته abbbba توسط ماشین پذیرفته میشود اما این رشته به صورت تناوبی دارای ab نیست (حذف گزینه 3).
بررسی گزینه 4: رشته ab و ba به زبان این گزینه تعلق دارند اما این رشتهها توسط ماشین پذیرفته نمیشوند (حذف گزینه 4).
آسان
در گرامر مستقل از متن $G$ هیچ سمبل غیرپایانی $A$ وجود ندارد به طوری که $A\ {{\stackrel{+}{\Rightarrow}}} \ UAV$ کدام گزینه صحیح است؟
زبانهای مستقل از متن
1 یک زبان منظم را معرفی میکند.
2 زبان معادل آن منظم نیست.
3 زبان معادل آن بیپایان و نامنظم است.
4 زبان معادل آن بیپایان ولی منظم است.
با توجه به فرض مسئله میفهمیم که هیچ متغیر به خود بازگشت نمیکند یعنی هیچ لوپی نخواهیم داشت و این بدان معناست که زبان حاصل متناهی خواهد شد. همچنین میدانیم که زبان متناهی منظم است در نتیجه گزینه 1 صحیح است.
متوسط
گرامر $G$ و رشتههای $w_1$ و $w_2$ به شرح زیر مفروضاند:
زبانهای مستقل از متن
کدام گزینه صحیح است؟
$S\rightarrow ac \; BdeA|BAB$
$B\rightarrow a\;Sb| ae|\varepsilon$
$A\rightarrow a\;Ab|b|\varepsilon$
$w_1=acaaca\;bbdebdeb$
$w_2=acaacaaeebdebbdeabb$
1 $w_1\notin L\left(G\right),\ \ w_2\in L(G)$
2 $w_1\in L\left(G\right),\ \ w_2\in L(G)$
3 $w_1\in L\left(G\right),\ \ w_2\notin L(G)$
4 $w_1\notin L\left(G\right),\ \ w_2\notin L(G)$
اگر کمی به رشته دوم ($w_2$) دقت کنیم میبینیم که این رشته دارای 2 حرف e پشت سر هم است و این در حالیست که این گرامر قادر به تولید دو حرف e پشت سر هم نیست در نتیجه بدون بررسی کردن میتوان گفت که این رشته متعلق به زبان نیست (حذف گزینه 1 و 2). برای رشته اول نمیتوان همچنین استدلالی به کار برد در نتیجه تنها راه این است که ببینیم آیا میتوان این رشته را توسط گرامر تولید کرد یا خیر.
\[S{{\stackrel{1}{\Rightarrow}}}acBdeA{{\stackrel{2}{\Rightarrow}}}acaSbdeA{{\stackrel{1}{\Rightarrow}}}acaacBdeAbdeA{{\stackrel{2}{\Rightarrow}}}acaaca\underbrace{S}_{BAB}bde\underbrace{A}_{\lambda }bde\underbrace{A}_{b}{{\stackrel{*}{\Rightarrow}}}acaacaSbdebdeb{{\stackrel{1}{\Rightarrow}}}acaaca\underbrace{B}_{\lambda }\underbrace{A}_{b}\underbrace{B}_{\lambda }bdebdeb{{\stackrel{*}{\Rightarrow}}}acaacabbdebdeb\]
همانطور که میبینیم رشته اول ساخته شد پس این رشته به زبان تعلق دارد (حذف گزینه 4).
دشوار
زبانهای $L_1$ و $L_2$ با تعاریف زیر را در نظر میگیریم: ${w}_\mathbf{1},{w}_\mathbf{2}\in\left\{{a},{b}\right\}^\ast$
خصوصیات زبانهای مستقل از متن
$L_1 = \{w_1 w_2| |w_1| = |w_2| , w_1\neq w_2 \}$
$L_2 = \{ w_1 w_2 | w_1,w_2 \in \{0,1\}^* , n_a (w_1) = n_b (w_2) \}$
1 $L_1$ از نوع آزاد از متن است ولی $L_2$ از این نوع نیست.
2 $L_2$ و $L_1$ هر دو آزاد از متن هستند.
3 $L_2$ از نوع آزاد از متن است ولی $L_1$ از این نوع نیست.
4 هیچ کدام از دو زبان آزاد از متن نیست.
بررسی زبان ${L}_\mathbf{1}$:
این زبان شامل رشتههایست به طول زوج که هر رشته شامل دو قسمت است که این دو قسمت طول برابری دارند اما باهم برابر نیستند یعنی حداقل 1 حرف در این دو زیر رشته در جایگاه یکسان وجود دارد که برابر هم نیستند که نتیجه آن باعث عدم برابری دو زیر رشته میشود. میتوان گفتهمان را به صورت زیر بیان کنیم.
\[w={\left(a+b\right)}^ma\overbrace{{\left(a+b\right)}^m}^{\curvearrowleft }\overbrace{{\left(a+b\right)}^n}^{\curvearrowright }b{\left(a+b\right)}^n\]
همانطور که میبینید جای دو عبارت را به دلیل یکی بودن پایهها عوض کردم. حال به نوشتن گرامر میپردازیم.
$ S\rightarrow S_1S_2\ |\ S_2S_1\ $
$S_1\rightarrow aS_1a\ |\ bS_1b\ |\ a$
$S_2\rightarrow aS_2a\ |\ bS_2b\ |b$
در نتیجه این زبان مستقل از متن است.
بررسی زبان ${L}_\mathbf{2}$:
این زبان برابر $\sum^\ast$ است در نتیجه منظم و مستقل از متن است.
اثبات:
فرض کنید دو اشارهگر داریم. یک اشارهگر از انتهای رشته به سمت چپ حرکت کرده و تعداد bها را میشمارد و یک اشارهگر از ابتدای رشته به سمت راست حرکت کرده و تعداد aها را میشمارد و به اینصورت عمل میکند که در ابتدا اشارهگر انتهایی شروع به حرکت کرده تا به اولین b برسد. سپس میایستد تا اشارهگر ابتدایی حرکت کرده و به اولین a برسد . همینطور ادامه میابد تا اشارهگرها به هم برسند یعنی اشارهگر اول در اندیس k و اشارهگر دوم در اندیس $k+1$ باشند. حال 2 حالت امکان دارد رخ دهد، یا تعداد bهایی که اشارهگر دوم شمارش کرده با تعداد aهایی که اشارهگر اول شمارش کرده برابر است که در این صورت از اشاره اگر اول به قبل را به نام $w_1$ نام گذاری میکنیم و از اشارهگر دوم به قبل را $w_2$. برای حالت دوم این امر مطرح است که تعداد bهای شمارش شده یکی بیشتر از aهاست (یا برعکس) که در این صورت میآییم اشارهگر دوم را یکی به عقب میبریم و اشارهگر اول را یکی به جلو میبریم و اینکار را تا جایی ادامه میدهیم که آن اختلاف 1 جبران شده و تعداد aها با تعداد bها برابر شود. روی هر رشتهای این الگوریتم قابل اجراست و صحیح عمل میکند در نتیجه روی همه رشتهها حاصل درست خواهد بود.
روش دوم: استفاده از دوره های نکته و تست درس های کنکور کامپیوتر
دوره های نکته و تست درس های کنکور کامپیوتر جهت تسلط دانشجویان بر تستهای کنکور تهیه شدهاند. این دورهها شامل تمامی تستهای کنکور آن درس به همراه پاسخنامه تشریحی است. برای آشنایی بیشتر با هر دوره میتوانید از لینکهای زیر استفاده کنید.
پاسخ نامه کنکور ارشد کامپیوتر ۱۳۹۰
اگر صرفاً به پاسخهای کلیدی کنکورهای کامپیوتر نیاز دارید، میتوانید تمامی آنها را از صفحه دفترچه سوالات کنکور ارشد مهندسی کامپیوتردانلود سوالات کنکور ارشد کامپیوتر دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند دانلود کنید.
دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند دانلود کنید.
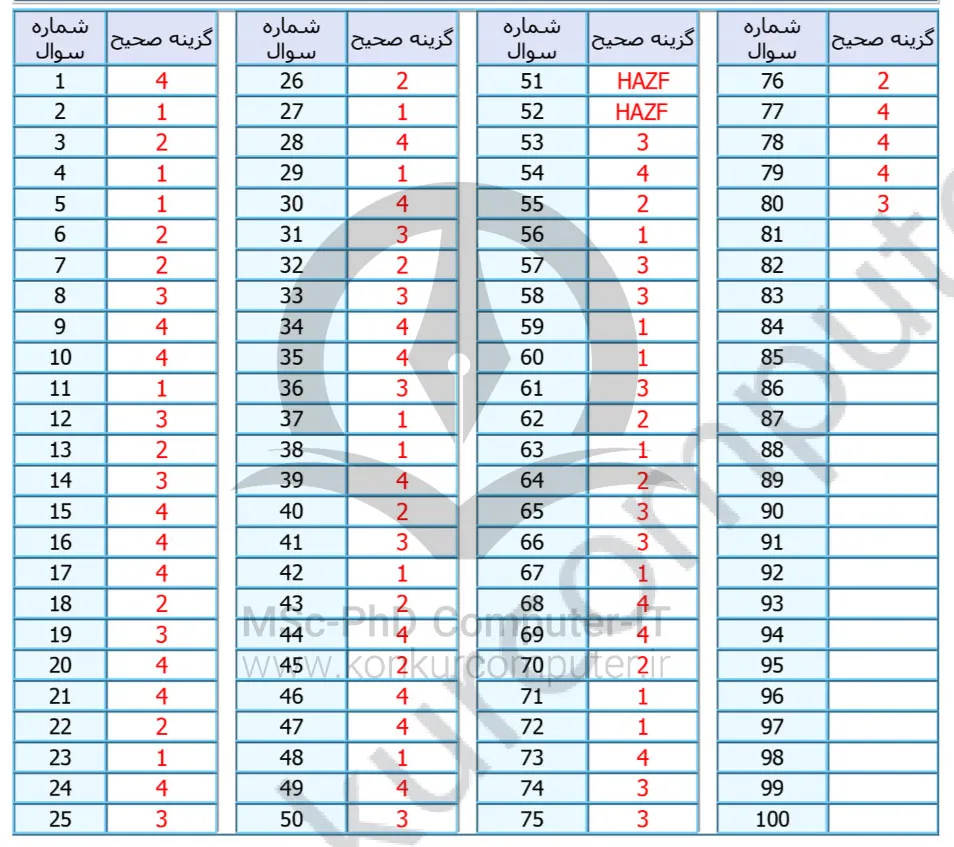
کلید کنکور ارشد کامپیوتر ۱۳۹۰
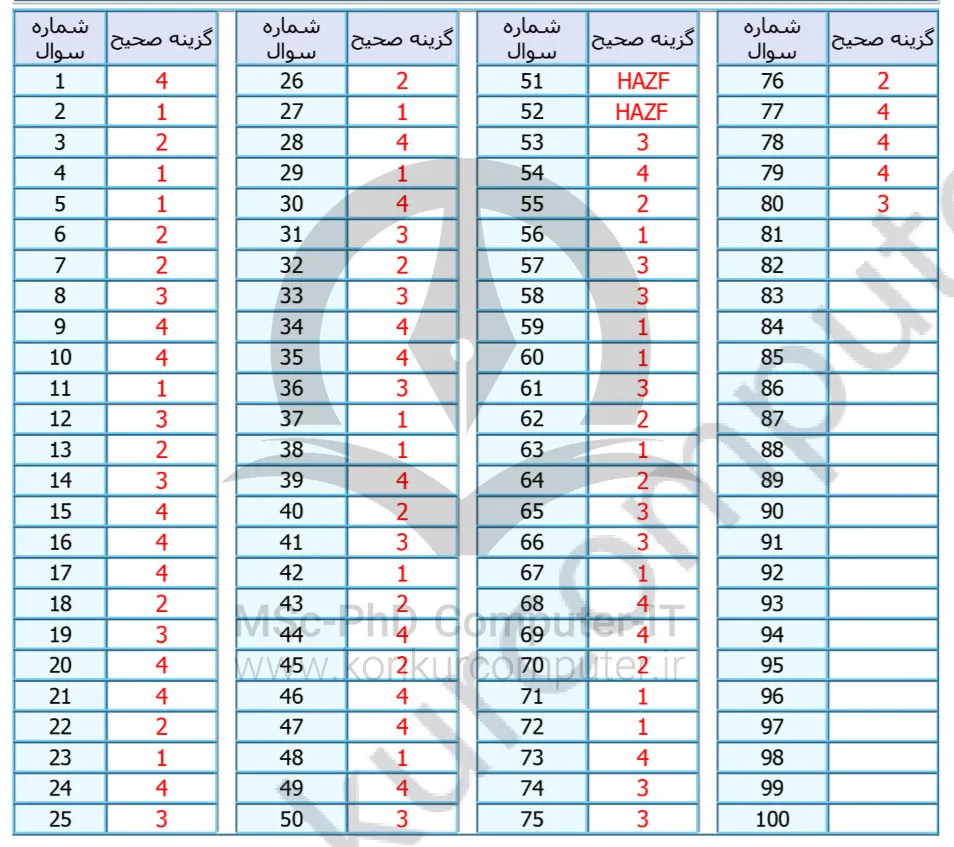
پاسخ کلیدی کنکور ارشد کامپیوتر سال ۱۳۹۰ برای هر دو دفترچه در زیر قرار گرفته است. کلید کنکور ارشد کامپیوتر در واقع همان پاسخنامهای است که سازمان سنجش برای کنکور ارائه میکند.
جمعبندی
داوطلبان آزمون کارشناسی ارشد کامپیوتر برای پاسخگویی به سوالات کنکور ارشد کامپیوتر نیاز به دانش عمیق و تسلط بر مباحث مورد نظر دارند و لازم است که از منابع مناسبی استفاده کنند پس استفاده از دوره نکته و تست و پلتفرم آزمون را به شما پیشنهاد میکنیم.
به چه روش هایی میتوانم به پاسخ تشریحی دفترچه های کنکور دسترسی داشته باشم؟
دو روش: (1) پلتفرم آزمون (۲) دورههای نکتهوتست
آیا منابعی برای دروس کنکور کامپیوتر وجود دارد؟
بله میتوانید از دورههای درس کنکور کامپیوتر استفاده کنید.
چگونه به پاسخ کلیدی کنکور ارشد کامپیوتر سال ۱۳۹۰ دسترسی داشته باشم؟
میتوانید پاسخ کلیدی تمامی کنکورهای کامپیوتر را از صفحه دفترچههای کنکور کامپیوتر دانلود کنید.

اشتراکhttps://www.konkurcomputer.ir/e979

 این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده، سیستم عاملمعرفی درس سیستم عامل – بهترین آموزش درس سیستم عامل در کشور
این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده، سیستم عاملمعرفی درس سیستم عامل – بهترین آموزش درس سیستم عامل در کشور درس سیستم عامل در این صفحه معرفی شده، همچنین بهترین آموزش درس سیستم عامل در کشور را میتوانید در این صفحه تهیه کنید، فصول و مراجع سیستم عامل نیز بررسی شده، الکترونیک دیجیتالمعرفی درس الکترونیک دیجیتال
درس سیستم عامل در این صفحه معرفی شده، همچنین بهترین آموزش درس سیستم عامل در کشور را میتوانید در این صفحه تهیه کنید، فصول و مراجع سیستم عامل نیز بررسی شده، الکترونیک دیجیتالمعرفی درس الکترونیک دیجیتال درس الکترونیک دیجیتال در تمامی دانشگاههای جهان به منظور آشنایی با مبانی الکترونیک و سختافزار و تکنولوژیهای استفاده شده از زمان پیدایش کامپیوتر تا کنون تدریس میشود و نظریه زبان ها و ماشین هادرس نظریه زبان ها و ماشین ها
درس الکترونیک دیجیتال در تمامی دانشگاههای جهان به منظور آشنایی با مبانی الکترونیک و سختافزار و تکنولوژیهای استفاده شده از زمان پیدایش کامپیوتر تا کنون تدریس میشود و نظریه زبان ها و ماشین هادرس نظریه زبان ها و ماشین ها این صفحه عالی به معرفی درس نظریه زبانها و ماشینها پرداخته است، همچنین به اهمیت درس نظریه در کنکور ارشد کامپیوتر، سرفصلها، معرفی مراجع و فیلمهای آموزشی این درس پرداخته است. به همراه پاسخ تشریحی آمده است:
این صفحه عالی به معرفی درس نظریه زبانها و ماشینها پرداخته است، همچنین به اهمیت درس نظریه در کنکور ارشد کامپیوتر، سرفصلها، معرفی مراجع و فیلمهای آموزشی این درس پرداخته است. به همراه پاسخ تشریحی آمده است: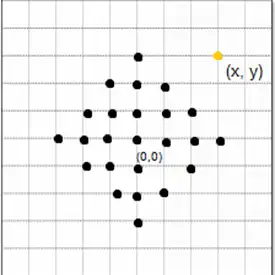



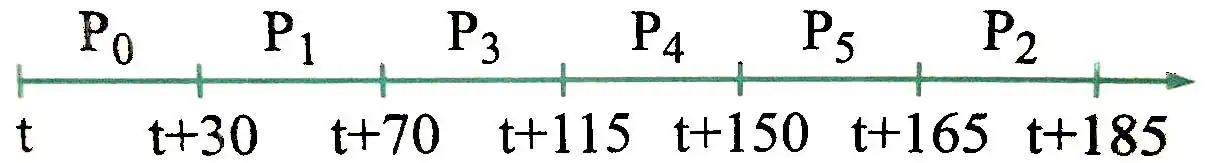

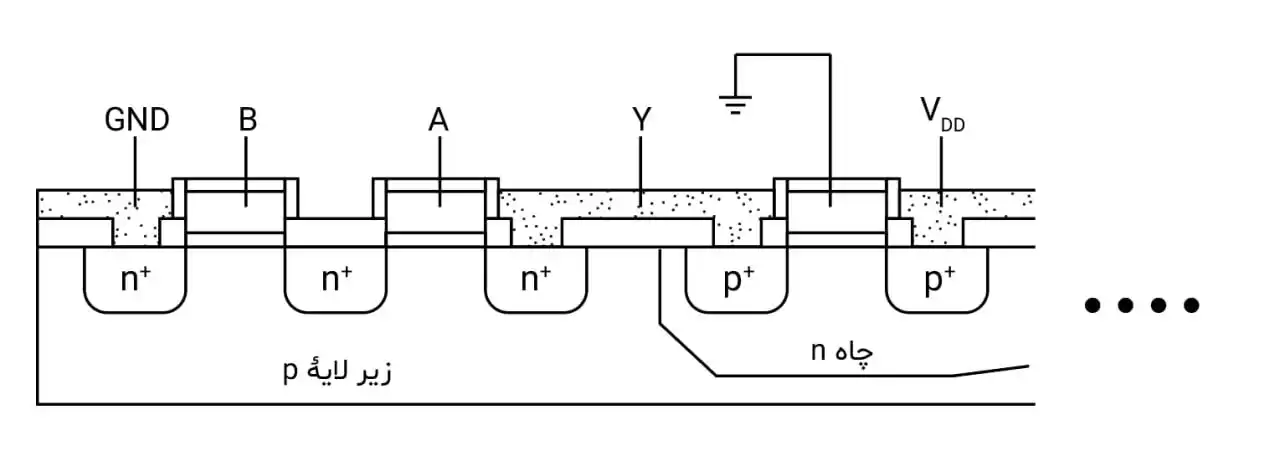
 بنابراین گزینه 4 صحیح است.
بنابراین گزینه 4 صحیح است.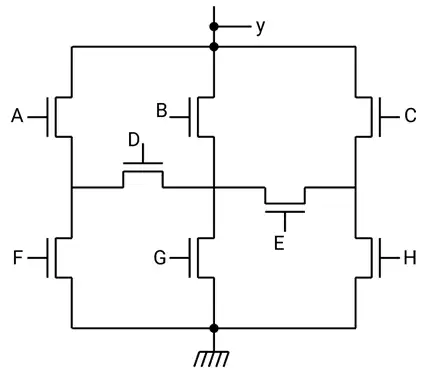

 از نگاه دانشجویان، قدرت بیان فوق العاده استاد رضوی و پوشش ۱۰۰ درصدی تمامی سرفصلها، نکات و تستها، ویدیوهای حل تست ساختمان داده و طراحی الگوریتم را به بهترین ویدیو حل تست کشور در درس ساختمان و الگوریتم تبدیل کرده است. این فیلم پرطرفدارترین و پرفروشترین فیلم حل تست ساختمان داده و الگوریتم کشور است و هر سال بیش از ۶۰۰۰ نفر این فیلم را تهیه میکنند
از نگاه دانشجویان، قدرت بیان فوق العاده استاد رضوی و پوشش ۱۰۰ درصدی تمامی سرفصلها، نکات و تستها، ویدیوهای حل تست ساختمان داده و طراحی الگوریتم را به بهترین ویدیو حل تست کشور در درس ساختمان و الگوریتم تبدیل کرده است. این فیلم پرطرفدارترین و پرفروشترین فیلم حل تست ساختمان داده و الگوریتم کشور است و هر سال بیش از ۶۰۰۰ نفر این فیلم را تهیه میکنند
 بهترین دوره نکته و تست هوش مصنوعی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست هوش و نحوه استفاده از نکته و تست هوش مصنوعی گفته شده
بهترین دوره نکته و تست هوش مصنوعی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست هوش و نحوه استفاده از نکته و تست هوش مصنوعی گفته شده
 دوره نکته و تست پایگاه داده و ویژگیها و اهمیت دوره نکته و تست پایگاه داده و نحوه استفاده صحیح از نکته و تست پایگاه داده کنکور ارشد کامپیوتر و آیتی در این صفحه عالی توضیح داده شده است
دوره نکته و تست پایگاه داده و ویژگیها و اهمیت دوره نکته و تست پایگاه داده و نحوه استفاده صحیح از نکته و تست پایگاه داده کنکور ارشد کامپیوتر و آیتی در این صفحه عالی توضیح داده شده است
 بهترین دوره نکته و تست سیستم عامل در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست سیستم های عامل و نحوه استفاده از نکته و تست سیستم عامل گفته شده
بهترین دوره نکته و تست سیستم عامل در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست سیستم های عامل و نحوه استفاده از نکته و تست سیستم عامل گفته شده
 بهترین دوره نکته و تست شبکه کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست شبکه های کامپیوتری و نحوه استفاده از نکته و تست شبکه گفته شده
بهترین دوره نکته و تست شبکه کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست شبکه های کامپیوتری و نحوه استفاده از نکته و تست شبکه گفته شده
 دوره نکته و تست نظریه زبان ها و ماشین ها در این صفحه قرار گرفته و ویژگی ها و اهمیت دوره نکته و تست نظریه زبان ها و ماشین ها بررسی شده است
دوره نکته و تست نظریه زبان ها و ماشین ها در این صفحه قرار گرفته و ویژگی ها و اهمیت دوره نکته و تست نظریه زبان ها و ماشین ها بررسی شده است
 دوره نکته و تست سیگنال و سیستم و ویژگیهای نکته و تست سیگنال و نحوه استفاده صحیح از نکته و تست سیگنال کنکور ارشد کامپیوتر در این صفحه عالی توضیح داده شده
دوره نکته و تست سیگنال و سیستم و ویژگیهای نکته و تست سیگنال و نحوه استفاده صحیح از نکته و تست سیگنال کنکور ارشد کامپیوتر در این صفحه عالی توضیح داده شده
 بهترین دوره نکته و تست مدار منطقی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست مدار منطقی و نحوه استفاده از نکته و تست مدار منطقی گفته شده
بهترین دوره نکته و تست مدار منطقی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست مدار منطقی و نحوه استفاده از نکته و تست مدار منطقی گفته شده
 بهترین دوره نکته و تست الکترونیک دیجیتال کشور در این صفحه معرفی شده و اهمیت دوره نکته و تست الکترونیک دیجیتال و نحوه استفاده صحیح از دوره بیان شده است
بهترین دوره نکته و تست الکترونیک دیجیتال کشور در این صفحه معرفی شده و اهمیت دوره نکته و تست الکترونیک دیجیتال و نحوه استفاده صحیح از دوره بیان شده است
 بهترین دوره نکته و تست ریاضیات گسسته کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست گسسته و نحوه استفاده از نکته و تست گسسته گفته شده
بهترین دوره نکته و تست ریاضیات گسسته کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست گسسته و نحوه استفاده از نکته و تست گسسته گفته شده
 دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند دانلود کنید.
دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند دانلود کنید.












































