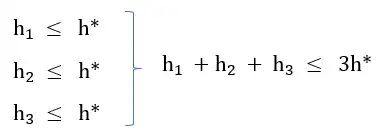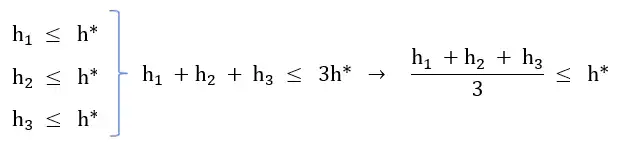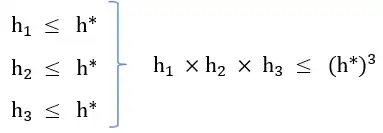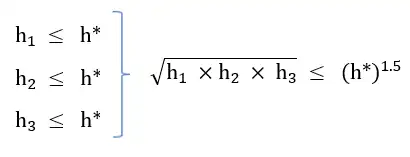در این صفحه نمونه سوالات هوش مصنوعی با پاسخ تشریحی برای شما عزیزان قرار داده شده است، سعی شده مثال های هوش مصنوعی تمامی مباحث را در بر گیرد. در صورتی که علاقه دارید تا بیشتر با درس هوش مصنوعی آشنا شوید و فیلم های رایگان هوش مصنوعی را مشاهده کنید به صفحه معرفی و بررسی الکترونیک دیجیتالمعرفی درس الکترونیک دیجیتال
درس الکترونیک دیجیتال در تمامی دانشگاه‌های جهان به منظور آشنایی با مبانی الکترونیک و سخت‌افزار و تکنولوژی‌های استفاده شده از زمان پیدایش کامپیوتر تا کنون تدریس میشود مراجعه کنید.
قبل از اینکه به ادامه این مقاله بپردازیم توصیه می‌کنیم که فیلم زیر که در خصوص تحلیل و بررسی درس هوش مصنوعی است را مشاهده کنید، در این فیلم توضیح داده شده که فیلم درس هوش مصنوعی برای چه افرادی مناسب است و همین طور در خصوص فصول مختلف درس هوش مصنوعی و اهمیت هر کدام از فصول آن صحبت شده است.
در ادامه این مقاله ابتدا فیلم های رایگان هوش مصنوعی که به آنها نیاز دارید و سپس نمونه سوالات هوش مصنوعی در اختیارتان قرار گرفته است.
فیلم های رایگان آموزش هوش مصنوعی که به آنها نیاز دارید
در حال حاضر فیلم آموزش هوش مصنوعی استاد رضوی پرطرفدارترین و پرفروش‌ترین فیلم آموزشی هوش مصنوعی کشور است و هر سال اکثر داوطلبان کنکور ارشد کامپیوتر این فیلم را تهیه می‌کنند.
هوش مصنوعی جلسه 1
هوش مصنوعی جلسه 2
هوش مصنوعی جلسه 3
هوش مصنوعی جلسه 4
نکته و تست هوش مصنوعی جلسه 1
جواب تشریحی هوش مصنوعی کنکور ارشد کامپیوتر 1403
خرید فیلم های کامل هوش مصنوعی
فیلم درس هوش مصنوعی
به‌وقت بهار تا ۵ اردیبهشت
35%
رامین رضوی
60 ساعت
فیلم نکته و تست هوش مصنوعی
به‌وقت بهار تا ۵ اردیبهشت
35%
رامین رضوی
۳۰ ساعت
مونه سوالات فصل عامل ها و محیط ها درس هوش مصنوعی
متوسط کدام عبارت در مورد خصوصیات محیط (environment)، درست است؟ عامل ها و محیط ها
گزینه 3 صحیح است.
گزینه ۱ : مشاهده پذیر بودن محیط به این معنی است که عامل بتواند هر اطلاعاتی از محیط که به آن نیاز دارد را با حسگرهایش بدست آورد و این ربطی به اینکه محیط پویا است یا ایستا ندارد.
گزینه ۲ : اساسا محیط های که شانس در آنها وارد میشود دیگر قطعی نیستند مثلا در بازی منچ محیط مشاهده پذیر کامل است به این معنی که محیط بازی برای هر بازیکن مشخص است اما این محیط بدلیل عنصر شانس (همان تاس) که در حرکات دخیل است محیطی غیر قطعی است.
گزینه ۳ : ناشناخته بودن محیط به این معنی است که حداقل یک کنش وجود دارد که عامل نتیجه انجام آن در محیط را نمی‌داند و این حالت می‌تواند در محیط مشاهده پذیر کامل نیز رخ دهد.
گزینه ۴ : محیط اپیزودیک یک محیط رویدادی است و شامل کنش‌هایی میشود که قابل تقسیم به اپیزودهای مستقل از هم هستند و تعریف ارائه شده در صورت سوال معادل برای محیط های ترتیبی است نه اپیزودیک.
آسان یک عامل ربات فوتبالیست در چه محیطی قرار دارد؟ عامل ها و محیط ها
محیط پویا است چون در زمانی که عامل در حال فکر کردن و تصمیم گیری است وضعیت محیط (جای بازیکن‌ها و توپ و ...) می‌تواند تغییر کند. محیط غیر قطعی است چون وضعیت حاصل از انجام هر عمل، علاوه بر آن عمل و وضعیت فعلی، به عوامل دیگر (مثل حرکت بازیکن‌های دیگر) نیز بستگی دارد. محیط پیوسته است: مکان بازیکن‌ها و توپ و همینطور زمان، کمیت‌های پیوسته‌اند. محیط ترتیبی است: تصمیمات عامل در هر لحظه بر روی تصمیمات او در آینده موثر خواهد بود.
آسان یک عامل مبتنی بر هدف (goal-based) در مسئله‌ای با اهداف نسبتاً متناقض روبه‌روست. برای یافتن بهترین عمل چه تغییری در این عامل لازم است؟ عامل ها و محیط ها
گزینه 3 صحیح است.
در این مسئله عامل مبتنی بر هدف با اهدافی متناقض رو به رو است مثل حالتی که نیاز داریم که یک جاروبرقی هم یک خانه را به خوبی تمیز کند و هم سرعت بالایی داشته باشد که با هم در تناقض هستند. در این گونه مسائل عامل سودگرا می‌تواند عملکرد خوبی داشته باشد چرا که ویژگی این نوع عامل‌ها و مزیت آنها نسبت به عامل هدف‌گرا این است که وجود اهداف متناقض و همچنین وجود اهدافی که قطعیت در رسیدن به آنها وجود ندارد مشکلی ایجاد نمی‌کند و از طرفی مهم‌ترین رکن در این نوع عامل ها تعیین درست تابع سودمندی است که براساس معیارهای سودمندی برای عامل تعریف میشود. پس در صورتی‌که این عامل خود را به تابع مطلوبیت (سودمندی) مجهز کند می‌تواند بهترین عملکرد را داشته باشد.
نمونه سوالات فصل الگوریتم های جستجوی ناآگاهانه درس هوش مصنوعی
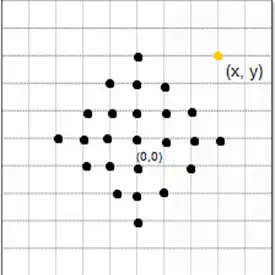
دشوار روی یک توری n*n که هر خانه به چهار همسایه خود متصل است، خانه میانی را نقطه شروع جستجو و نقطه $\left(\circ \ ,\ \circ \right)$ در نظر می‌گیریم. گره هدف در موقعیت $\left(\mathrm{X\ ,\ Y}\right)$ است. در این گراف الگوریتم جستجوی A بدون تست تکراری بودن حالات، حداکثر $\left(\left({\mathrm{4}}^{\mathrm{X\ +\ Y\ +\ }\mathrm{1}}-\ \mathrm{1}\right)\ / \, \mathrm{3}\right)\mathrm{-}\mathrm{1}$ گره و الگوریتم جستجوی B با تست تکراری بودن حالات، حداکثر $\mathrm{2}\left(\mathrm{X\ +\ Y}\right)\left(\mathrm{X\ +\ Y\ +\ }\mathrm{1}\right)\ -\mathrm{1}$ گره را قبل از یافتن جواب بسط می‌دهند. کدام یک از گزینه‌های زیر در مورد این دو الگوریتم صحیح است؟ الگوریتم های جستجوی ناآگاهانه
گزینه 2 صحیح است.
(نکته : در این تست فرض شده است که تست در الگوریتم BFS در زمان بسط انجام میشود)
در این سوال در ابتدا هر کدام از حالات جستجو درختی و گرافی را با روش DFS و BFS بررسی می‌کنیم.
۱- جستجوی A بدون تست تکراری بودن حالات (درختی)
آ) BFS
در جستجو اول سطح در هر مرحله با توجه به اینکه هر گره چهار فرزند دارد، فاکتور انشعاب ۴ است (چون تکرار هم داریم) و در هر مرحله تعداد گره‌های ۴ برابر میشود و در صورتی که بدانیم هدف در خانه (x,y)است داریم :
تعداد گره‌های بسط داده شده $=\mathrm{1\ +\ b\ +\ }b^{2\ }+\ ......+b^{d\ }-1\ =\ \frac{b^{d+1}\ -1}{b-1}\ \ \ \ -1\ =\ \frac{4^{x+y+1}-1\ }{3}\ -1$
نکته :
۱- آخر برای کم کردن خود گره هدف است.
از آنجایی که در هر مرحله به یکی از گره‌های مجاور می‌رویم و حرکت مورب نداریم می‌توان گفت d = x +y می‌باشد.
ب) DFS
جستجو اول عمق در صورتی که تکرار داشته باشیم در بدترین حالت ممکن است در حلقه بینهایت بیفتد و هیچگاه تمام نشود.
۲- جستجوی A با تست تکراری بودن حالات (گرافی)
آ) BFS
در این جستجو مطابق شکل زیر در هر مرحله یک دور به مربع اضافه میشود تا به هدف که در (x,y) قرار دارد برسیم. تعداد گره‌هایی که در هر مرحله بسط داده می‌شوند الگویی مطابق فرمول زیر دارند:
تعداد گره‌های بسط داده شده =
$ \mathrm{1+b+}2b+\dots \dots +\mathrm{bd\ -1}=1+4\left(1+2+\dots .+d\right)-1=1+\frac{4d\left(d+1\right)}{2}\ -1=2\left(x+y\right)\left(x+y+1\right)$
نکته :
۱- آخر برای کم کردن خود گره هدف است.
از آنجایی که در هر مرحله به یکی از گره‌های مجاور می‌رویم و حرکت مورب نداریم می‌توان گفت d = x +y می‌باشد.
ب) DFS
این روش در صورتی که تست تکراری بودن حالات را داشته باشیم در بدترین حالت همه گره‌های صفحه یعنی $n^2-1$ گره را بررسی میکند.
با توجه به صورت سوال و با توجه به مقادیر که در بالا بدست آوردیم بهترین گزینه برای این پاسخ این سوال گزینه دوم است.
دشوار فرض کنید برای مسئله‌ای با جستجوی اول پهنا (Breadth first) و تست هدف در لحظه تولید، نیاز به بسط دادن (expand) 32 گره باشد. اگر فاکتور انشعاب (branching factor) درخت جستجو ثابت باشد و عمق درخت برابر 5 و عمق هدف (goal) برابر 4 باشد، کدام یک از گزینه‌ها مقدار فاکتور انشعاب (b) را نشان میدهد؟ (فرض کنید ریشۀ درخت در عمق صفر $\left(\mathrm{\circ }\right)$ واقع شده است.) الگوریتم های جستجوی ناآگاهانه
گزینه 4 صحیح است.
در روش جستجو اول پهنا ابتدا گره ریشه بررسی میشود و سپس روی فرزندان آن یکی یکی تست هدف صورت می‌گیرد و به صف جهت بسط داده شدن اضافه می‌شوند. پس از آن در صورتی که به هدف نرسیده باشیم از ابتدای صف یک گره را انتخاب کرده و همین روند را تکرار می‌کنیم.
در صورت سوال گفته شده است که برای رسیدن به هدف در این مسئله ۳۲ گره بسط داده می‌شوند از طرفی عمق کلی درخت ۵ و عمق هدف ۴ می‌باشد اما بسته به محل قرارگیری هدف مسئله می‌تواند متفاوت باشد. در بهترین حالت (کمترین فاکتور انشعاب) گره هدف بعنوان اولین گره عمق ۴ تولید میشود و به هدف می‌رسیم و در بدترین حالت (بزرگترین فاکتور انشعاب) گره هدف آخرین گره عمق ۴ است که تولید میشود با این توضیحات تعداد گره‌های بسط داده شده در بهترین و بدترین حالت را براساس فاکتور انشعاب می‌توان به صورت زیر نوشت که عدد ۳۲ حتما باید در بین آنها باشد.
$1+b\ +\ b^2+\ 1\ \le \ 32\ \le \ 1+b\ +\ b^2+\ b^3$
که از روی حدود بالا می‌توان به $3 \le b \le 5$ رسید.
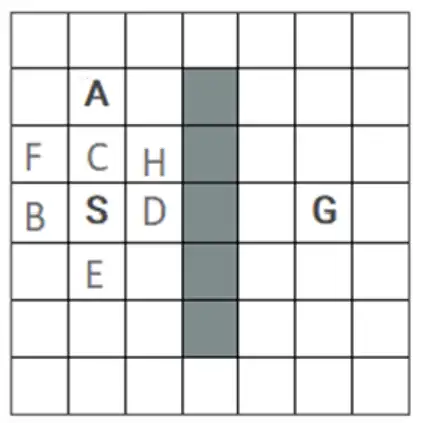
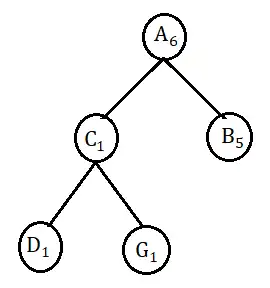
متوسط محیط زیر با وضعیت شروع S و وضعیت هدف G را در نظر بگیرید. فرض کنید خانه‌های خاکستری مسدود هستند و نمی‌توان به آنها وارد شد. همچنین در هر وضعیت چهار کنش بالا U، راست R، پایین D و چپ L با هزینه برابر قابل انجام هستند. اولویت انتخاب کنش‌ها هم در شرایط یکسان به ترتیب از راست به چپ D، R، U و L خواهد بود. اگر کنشی منجر به برخورد به خانه‌های مسدود یا دیوارها شود، عامل (agent) سر جایش می‌ماند. اگر جستجو گرافی (graph search) انجام شود، خانه A در شکل زیر چندمین گره برداشته شده از صف برای گسترش در روش‌های DFS و BFS خواهد بود؟ الگوریتم های جستجوی ناآگاهانه
| A | ||||||
| S | G | |||||
گزینه 2 صحیح است.
شکل زیر را در نظر بگیرید :
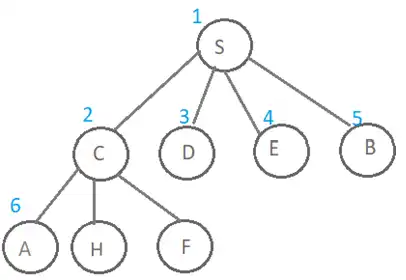
روش BFS :
درخت حاصل از جستجو به این روش و ترتیب بسط گره‌ها در ادامه نمایش داده شده است. همانطور که در شکل زیر مشخص است پس از S تمامی فرزندان آن بسط داده می‌شوند و درنهایت نوبت به فرزندان گره C می‌رسد و گره A از فرزندان این گره چون کنش UP اولویت بیشتر دارد زودتر به صف اضافه شده و در نتیجه زودتر هم نوبت به بسط آن می‌رسد و به عنوان گره ۶ ام بسط داده میشود.
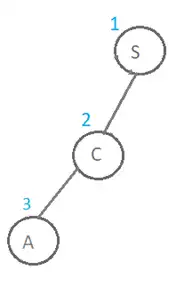
روش DFS :
درخت حاصل از جستجو به این روش و ترتیب بسط گره‌ها در ادامه نمایش داده شده است. همانطور که در شکل زیر مشخص است پس از S فرزند اول آن یعنی C و پس از آن گره A بسط پیدا میکند و در واقع گره A به عنوان گره ۳ ام بسط داده میشود.
اعداد بدست آمده در هیچکدام از گزینه‌ها موجود نیستند اما می‌توان با اغماض گزینه دوم را بعنوان پاسخ سوال در نظر گرفت.
آسان در جستجوی درختی (Tree-Search) با استفاده از روش‌های جستجوی ناآگاهانه (Uniformed) کدام مورد درست نیست الگوریتم های جستجوی ناآگاهانه
بررسی گزینه‌ها:
گزینه ۱:
الگوریتم IDS (Iterative Deepening Search) در هر مرحله تا یک لول مشخص جست‌وجوی DFS انجام میدهد و در مرحله بعدی یک سطح جلوتر می‌رود.
این الگوریتم بهینه بوده و نزدیکترین گره به ریشه پیدا میکند.
بیشترین حافظه لازم برابر عمقی است که برای یافتن بهینه‌ترین هدف (کم عمق‌ترین هدف) طی میکند و از مرتبه $O(bd)$ است.
این گزینه صحیح است.
گزینه ۲:
الگوریتم BFS بهینه عمل میکند و همیشه کم عمق‌ترین هدف را پیدا میکند.
حافظه لازم در هر عمقی که BFS در حال جست‌وجوی آن است از مرتبه $O(b^d)$ است که d عمق گره هدف بهینه (کم عمق‌ترین هدف) می‌باشد و b متوسط فرزندان هر گره (فاکتور انشعاب) است.
بنابراین بیشترین حافظه‌ای که BFS نیاز دارد نیز از این مرتبه است و همانطور که مشخص است این مرتبه نمایی است.
این گزینه نیز صحیح می‌باشد.
گزینه ۳:
مرتبه حافظه مورد نیاز در DFS، بر حسب عمقی که در آن در حال جست‌وجو است خطی است و بطورکلی مرتبه حافظه DFS از مرتبه $O(bm)$ است که m بیشترین عمق در درخت است، پس حافظه DFS بر حسب m خطی است نه بر حسب b. توجه کنید که این الگوریتم تضمین نمی‌کند که همیشه بهینه‌ترین هدف (کم عمق‌ترین هدف) را اول بیابد.
این گزینه غلط است و جواب این گزینه است.
گزینه ۴:
جست‌وجوی bidirectional از لحاظ حافظه مشابه BFS عمل میکند. این گزینه نیز صحیح است.
آسان در یک مسئله جستجو که گراف حالت آن یال‌هایی با وزن یکسان و مثبت دارد و حداکثر درجه گره‌های آن b است، از روش عمق اول (DFS) استفاده کرده‌ایم و گره هدفی را در ضمن جستجو در عمق d یافته‌ایم. برای اطمینان از اینکه این گره، حالت هدف بهینه است، حداکثر چند گره دیگر را باید مورد بررسی قرار دهیم؟ الگوریتم های جستجوی ناآگاهانه
گزینه 4 صحیح است.
در بدترین شرایط:
اگر گره هدف در عمق ۱ باشد ۱ گره قبل از آن نزدیک به ریشه قرار دارد (که خود ریشه است).
اگر گره هدف در عمق ۲ باشد $1+b$ گره قبل از آن نزدیک به ریشه قرار دارد.
اگر گره هدف در عمق ۳ باشد $1+b+b^2$ گره قبل از آن نزدیک به ریشه قرار داد.
به همین ترتیب اگر ادامه دهیم داریم:
اگر گره هدف در عمق d باشد $1+b+b^2+ \dots+b^{d-1}$ گره قبل از آن نزدیک به ریشه قرار داد.
بنابراین در نهایت با توجه به حاصل جمع دنباله‌های هندسی می‌توان گفت که در بدترین حالت $\frac{b^d-1}{b-1}$ گره قبل از گره هدف نزدیک به ریشه قرار دارند.
امّا توجه داشته باشید که براساس سؤال جست‌وجوی انجام شده از نوع DFS است. بنابراین اگر گره هدف در عمق d قرار داشته باشد، d گره قبل از آن (از جمله ریشه) تا الان جست‌وجو شده‌اند.
بنابراین ما در نهایت نیاز به جست‌وجوی $\frac{b^d-1}{b-1}$ گره داریم.
توجه: گزینه صحیح سؤال گزینه ۴ می‌باشد که با جواب ما به اندازه ۱ واحد اختلاف دارد. به نظر می‌آید این از مشکل طراحی سؤال است، چرا که برای مثال اگر در نظر بگیرید گره هدف در عمق ۱ باشد یعنی نزدیکترین حالت به ریشه دیگر نیازی به چک کردن گره دیگری برای مطمئن شدن از بهینه بودن آن نیست زیرا جواب بهینه‌تر از آن خود ریشه است که در ابتدا توسط DFS چک میشود.
نمونه سوالات فصل الگوریتم های جستجوی آگاهانه درس هوش مصنوعی
آسان نقطه ضعف روش جستجوی $(Iterative \; Deepening \; A^*) \; {IDA}^*$ در چیست؟ الگوریتم های جستجوی آگاهانه
گزینه 2 صحیح است.
روش IDA* روشی مشابه A* است که در جهت بهبود وضعیت مرتبه حافظه A* ارائه شده است و از ایده جستجو عمقی تکرار شونده استفاده میکند. پس مصرف حافظه این روش نسبتا خوب است و از آن‌جا که برمبنای A* و جستجو عمقی تکرار شونده است با همان شرط کامل بودن A* یعنی به شرط اینکه هزینه قدم‌ها مثبتِ بزرگتر از یک مقدار ثابت باشد و bf محدود باشد کامل نیز می‌باشد و کارایی خوبی دارد چرا که مرتبه زمانی آن مشابه A* است. در این روش درخت جستجو به صورت تکراری از ریشه تا زمانی که مقدار تمام گره ها از cutoff بیشتر شود به صورت عمقی ساخته میشود (به عبارتی همه گره هایی که f(n) آنها از cutoff کمتر است به صورت پیمایش عمقی بررسی می‌شوند). سپس در هر تکرار مقدار cutoff به کوچکترین مقدار f(n) گره‌های برگ (کوچکترین مقدار درون فرینج) بروزرسانی میشود و مجددا از اول روی گراف DFS انجام میشود و این کار تا جایی که به هدف برسیم ادامه می‌یابد. این روش از آن‌جا که در هر مرحله کل درخت جستجو را از ابتدا می‌سازد، گره‌های تکراری می‌سازد و بنابراین دوباره کاری دارد که یکی از نقطه ضعف‌های این الگوریتم محسوب میشود.
آسان می‌خواهیم با استفاده از روش جستجوی \( A^* \) پاسخ بهینه‌ی (optimal) مسأله‌ای را بیابیم، با فرض اینکه هر یک از سه تابع ابتکاری \( h_1 \),\( h_2 \),\( h_3 \) برای این منظور قابل استفاده باشد، کدام یک از توابع ترکیبی زیر نیز برای یافتن حل بهینه‌ی مسأله قابل استفاده خواهد بود؟ الگوریتم های جستجوی آگاهانه
گزینه 2 صحیح است.
ابتدا دو نکته را یادآوری می‌کنیم :
۱- در روش جستجوی A* :
- در حالت جستجوی درختی در صورتی که تابع هیوریستیک قابل قبول باشد، الگوریتم A* پاسخ بهینه را تضمین میکند .
- در حالت جستجوی گرافی در صورتی که تابع هیوریستیک سازگار باشد، الگوریتم A* پاسخ بهینه را تضمین میکند.
۲- در صورتی که چند تابع هیوریستیک قابل قبول داشته باشیم، میانگین حسابی و هندسی، max و min آنها نیز قابل قبول هستند چرا که در این توابع نیز هیچگاه مقدار h(n) تخمین زده شده برای یک گره بیشتر از مقدار اصلی هزینه مسیر آن گره تا گره هدف نمی‌شود.
با توجه به نکات بالا و با فرض جستجوی درختی باید بررسی کنیم که تابع هیوریستیک متناظر با کدام یک از گزینه ها قابل قبول است.
گزینه ۱: در این گزینه از مجموع سه تابع استفاده کرده است که طبق رابطه زیر هیچ تضمینی برای قابل قبول بودن آن نداریم.
گزینه ۲ : طبق رابطه زیر اثبات میشود که میانگین حسابی توابع قابل قبول، قابل قبول است.
گزینه ۳ : مشابه گزینه یک این گزینه نیز قابل قبول نیست.
گزینه ۴ : در این گزینه در صورتی که فرجه رادیکال به جای ۲ ، ۳ در نظر گرفته می‌شد تابعی قابل قبول به دست می‌آمد.
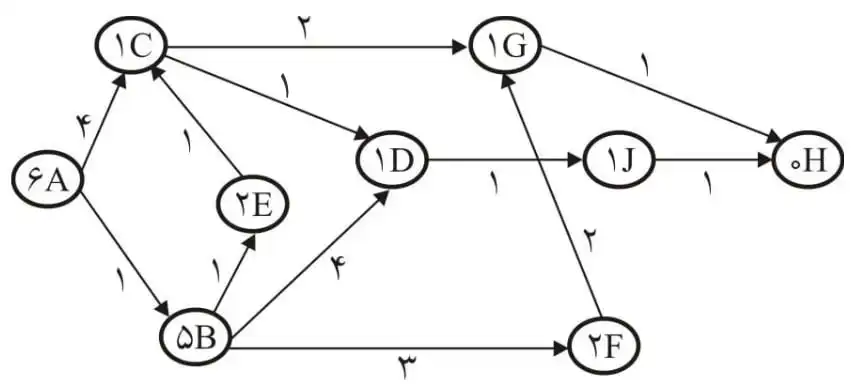
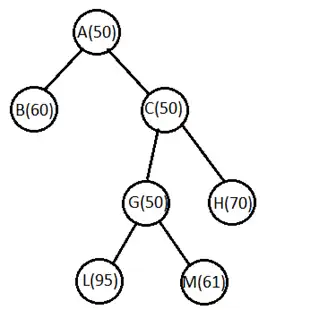
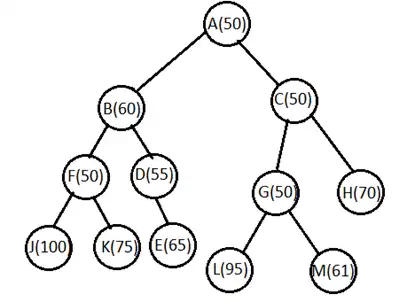
متوسط در صورت استفاده از روش تپه‌نوردی از طریق تندترین شیب (Steepest ascend hill climbing) با توجه به شکل زیر کدام یک از گزینه‌های زیر صحیح‌تر است؟ اعداد روی یال‌ها هزینه واقعی هر یال و اعداد داخل هر گره هزینه تخمینی آن گره تا گره‌ی هدف است. (A گره‌ی شروع و H گره هدف است.) الگوریتم های جستجوی آگاهانه
گزینه 1 صحیح است.
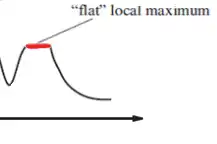
ابتدا به توضیح مفهوم فلات می‌پردازیم. فلات به ناحیه هموار و بهینه نسبت به همسایه‌های خود گفته میشود که در شکل زیر مشخص شده است.
روش تپه نوردی از طریق تندترین شیب به این صورت است که در هر مرحله از بین همسایه های گره جاری، بهترین همسایه که ارزش بیشتری دارد را انتخاب میکند و به آن همسایه می‌روند و این کار را تا آن‌جا انجام میدهد که گره جاری از تمام همسایه هایش ارزش بیشتری داشته باشد. در این سوال ارزش بیشتر متناسب با h کمتر است (به هدف نزدیک تر است) پس از گره A شروع می کنیم و از بین همسایه‌های آن به C که h کمتری دارد می‌رویم. پس از آن از باید ببینم که آیا همسایه های C دارای h کمتری هستند که از C به آنها برویم یا خیر. پس از بررسی طبق شکل زیر می‌بینیم که مقادیر h برای گره جاری (C) با مقادیر همسایه‌هایش یکی شده است و به عبارتی طبق توضیحی که در بالا از فلات بیان کردیم، جستجو به فلات برخورد کرده است و پاسخ سوال گزینه یک میشود. (در این سوال از وزن یال‌ها که در گراف داده است هیچ استفاده‌ای نمی‌شود)
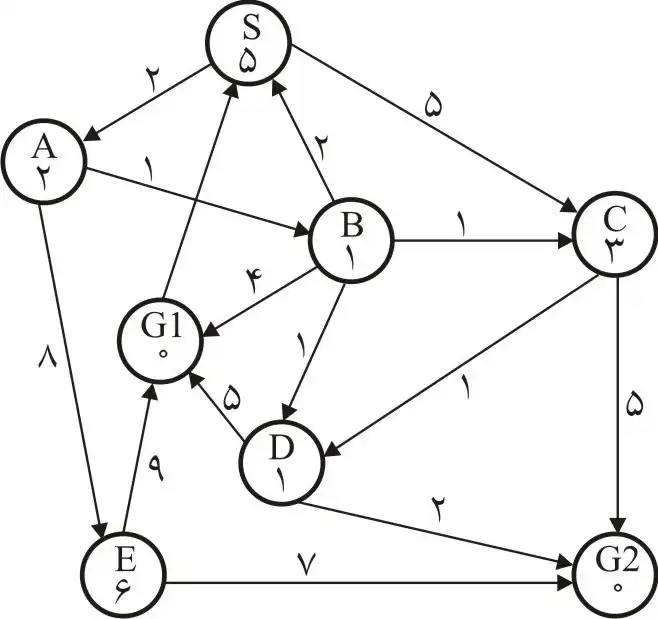
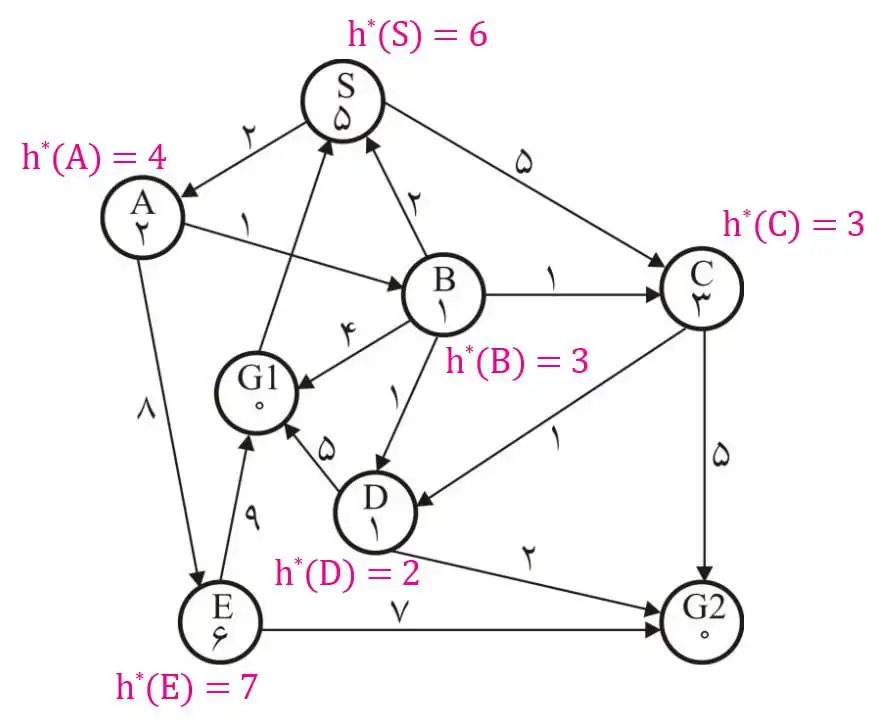
متوسط در گراف زیر حاصل جستجو با روش \( A^* \) کدام است؟ (نقطه شروع: S، اعداد روی یال‌ها و اعداد داخل گره‌ها هزینه تخمینی گره تا هدف است) الگوریتم های جستجوی آگاهانه
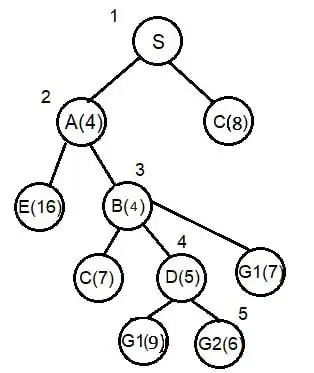
گزینه 4 صحیح است.
در این سوال، مسیر حاصل از جستجو با روش $A^\ast$ خواسته شده است و هم چنین در شکل دو هدف وجود دارد که مسیر بهینه رسیدن به G1 هزینه ۷ و مسیر بهینه رسیدن به G2 دارای هزینه ۶ است. در ابتدا بررسی می‌کنیم که آیا تابع هیوریستیک داده شده قابل قبول است یا نه چرا که در صورتی که قابل قبول باشد مسیر حاصل از جستجو $A^\ast$ همان مسیر بهینه است. از آن جایی که مسیر رسیدن به G2 هزینه کمتری دارد و $A^\ast$ در صورت قابل قبول بودن این مسیر را برمی‌گرداند، هزینه مسیر واقعی را با توجه به هدف G2 محاسبه می‌کنیم که در شکل زیر مشخص شده‌اند. با مقایسه مقادیر هیوریستیک با مقادیر واقعی می‌بینیم که تابع هیوریستیک داده شده قابل قبول است پس $A^\ast$ همان مسیر بهینه را که در شکل زیر مشخص شده است برمی‌گرداند.
روش دیگر حل سوال این بود که به صورت مستقیم الگورتیم $A^\ast$ را روی شکل اجرا کنیم که در شکل زیر درخت حاصل از آن نشان داده شده است (عدد ها ترتیب بررسی گره‌ها را نشان می‌دهند).
دشوار فرض کنید فضای جستجویی دارای پنج گره D ،C ،B ،A و Eباشد. جدول زیر فواصل واقعی این گره‌ها را از هم نشان میدهد. (وجود عدد در هر خانه جدول نشان‌دهندۀ این است که از گره مربوط به سطر به سمت گره مربوط به ستون مسیری به طول عدد وجود دارد.) اگر گره A گره شروع، گره E گره هدف و تابع h تابع مکاشفه‌ای تخمین فاصله گره تا هدف باشد، کدام یک از گزینه‌های زیر صحیح است؟ الگوریتم های جستجوی آگاهانه
| E | D | C | B | A | |
| 2 | 8 | 10 | A | ||
| 2 | 2 | 10 | B | ||
| 6 | 2 | 8 | C | ||
| 9 | 2 | 2 | D | ||
| 9 | 6 | 2 | E |
گزینه 3 صحیح است.
ابتدا گرافی که نشان‌دهنده فواصل داده شده در جدول است را رسم می‌کنیم سپس به بررسی گزینه‌ها می‌پردازیم هم چنین می‌دانیم که یک هیوریستیک قابل قبول است اگر شرط $h \le h \ast$ برای همه گره‌های آن برقرار باشد.
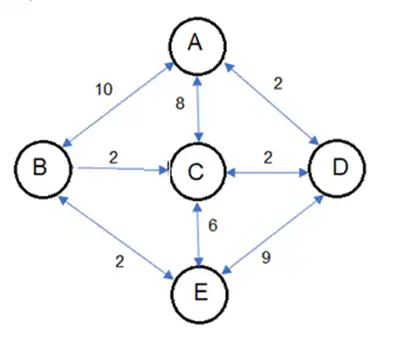
گزینه ۱ : در این گزینه h(C)=5, h(B)=1 , h(D)=8 داده شده است از طرفی با توجه به گراف بالا h*(C)=6, h*(B)=2 و h*(D)=8 می‌باشد پس شرط قابل قبول بودن برای این هیوریستیک برقرار است اما این هیوریستیک شرط سازگاری را ندارد چرا که برای مثال h(D) > h(C) + c(D,C) = h(C) + 2 می‌باشد پس این گزینه نادرست است.
گزینه ۲ : در این گزینه h(C)=6, h(B)=3 , h(D)=9 داده شده است مطابق گزینه قبل h*(C)=6, h*(B)=2 و h*(D)=8 می‌باشد پس شرط قابل قبول بودن برای این هیوریستیک برقرار نیست و در مورد سازگاری آن به دلیل اینکه داریم h(D) > h(C) + c(D,C) = h(C) + 2 این هیوریستیک ناسازگار است و این گزینه نیز نادرست است.
گزینه ۳ : در این گزینه h(C)=5, h(B)=1 , h(D)=8 داده شده است و شرط قابل قبول بودن برای این هیوریستیک برقرار است اما همانطور که در گزینه یک اشاره شد این هیوریستیک ناسازگار است پس این گزینه که فقط به قابل قبول بودن این تابع اشاره میکند درست است.
گزینه ۴ : در این گزینه h(C)=3, h(B)=3 , h(D)=8 داده شده است از طرفی می‌دانیم در صورتی که یک تابع هیوریستیک یکنواخت باشد پس حتما قابل قبول هم هست اما در صورت سوال اشاره شده است که قابل قبول نیست در نتیجه این گزینه نادرست میشود.
نکته : در هیچکدام از گزینه ها به h(A) اشاره نشده است و در این سوال فرض کردیم که هیوریستیک این گره درست و موجب قابل قبول نشدن یا ناسازگاری نمی‌شود.
آسان در الگوریتم Simulated Annealing در صورتی که دما بالا باشد کدام یک از عبارات زیر صحیح است؟ الگوریتم های جستجوی آگاهانه
الگوریتم شبیه‌سازی ذوب شده در واقع ترکیب تپه‌نوردی و قدم برداری تصادفی است.
در این الگوریتم در هر مرحله پارامتر دما (T) تنظیم میشود و در صورتی که دما به صفر برسد گره جاری به عنوان جواب نهایی برگردانده میشود. این الگوریتم در هر مرحله یک گره تصادفی از همسایه‌های گره جاری انتخاب میشود و اختلاف ارزش گره انتخابی با گره جاری سنجیده میشود($\triangle E$). چنانچه ارزش گره انتخابی بیشتر از گره جاری باشد به گره انتخابی رفته و مراحل را دوباره تکرار می‌کنیم اما اگر از گره جاری ارزش کمتری داشته باشد با احتمال $e^{\frac{\triangle E}{T}}$ به گره انتخابی می‌رویم، پایه اصلی این الگوریتم استفاده از مفهوم دما است به این معنی که هر چه دما بالاتر باشد احتمال رفتن به گره بدتر از گره جاری بیشتر میشود و هر چه دما پایین‌تر باشد این احتمال کاهش می‌یابد، سپس چه به گره بدتر برویم و چه نرویم مراحل را دوباره تکرار می‌کنیم و یک گره دیگر را به صورت تصادفی انتخاب می‌کنیم.
پاسخ سوال :
اگر دما به سمت بی نهایت میل کند الگوریتم شبیه‌سازی ذوب با احتمال بیشتری حالاتی را که وضعیت بدتری دارند انتخاب میکند و در نتیجه حالات بیشتر به عنوان گزینه‌های جست‌وجو مدنظر قرار می‌گیرند، این رفتار شبیه به رفتار در جست‌وجوی عمومی حالات می‌باشد. همچنین چون در سؤال گفته نشده که دما حتما بینهایت است بنابراین همچنان احتمالی هم برای انتخاب حالات بهتر وجود دارد که در جست‌وجو‌های محلی مثل تپه نوردی به این صورت عمل میشود. بنابراین هر دو نوع جست‌وجو با احتمال مشخصی انجام می‌شوند و گزینه ۴ صحیح است.
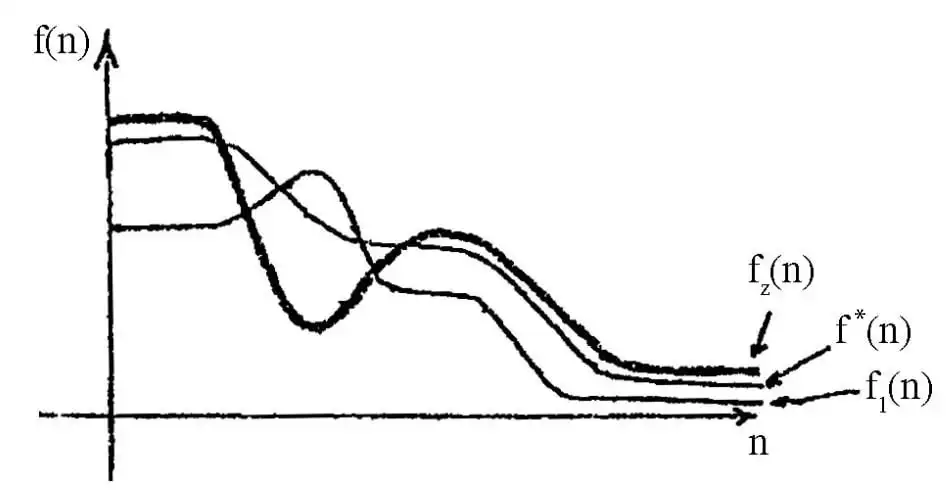
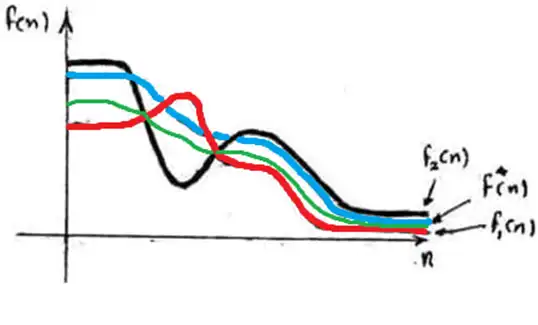
متوسط در جستجوی \( {A}^* \) در صورت استفاده از کدام تابع مکاشفه‌ای تضمین پیدا کردن جواب بهینه وجود دارد؟ الگوریتم های جستجوی آگاهانه
گزینه 4 صحیح است.
در روش جستجوی A* :
در حالت جستجوی درختی در صورتی که تابع هیوریستیک قابل قبول باشد، الگوریتم A* پاسخ بهینه را تضمین میکند .
در حالت جستجوی گرافی در صورتی که تابع هیوریستیک سازگار باشد، الگوریتم A* پاسخ بهینه را تضمین میکند.
با توجه به نکته بالا در صورتی که فرض کنیم روش جستجوی سوال درختی باشد باید به دنبال گزینه‌ای باشیم که بیانگر تابع مکاشفه‌ای قابل قبول باشد.
گزینه ۱ : این تابع که در شکل با رنگ قرمز نشان‌داده شده است خاصیت قابل قبول بودن (یعنی $\forall m \ f(n) \le f *(n)$) را ندارد چرا که در بعضی از قسمت‌ها از خط آبی که نشان‌دهنده مقدار واقعی $(f*(n))$ است بالاتر رفته است.
گزینه ۲ : این تابع که با خط مشکی نمایش داده شده است نیز خاصیت قابل قبول بودن را ندارد چرا که در بعضی از قسمت‌ها از خط آبی که نشان‌دهنده مقدار واقعی یعنی $f*(n)$ است بالاتر رفته است.
گزینه ۳ : هر کدام از توابع $f_1(n)$ و $f_2(n)$ به تنهایی قابل قبول نیستند در نتیجه جمع آنها نیز نمی‌تواند قابل قبول باشد (البته چون در این حالت مقدار برد توابع مثبت است توانستیم چنین نتیجه‌ای بگیریم)
گزینه ۴ : تابع این گزینه به صورت حدودی معادل خط سبز رنگ نشان داده شده در شکل زیر است. همانطور که مشاهده می‌کنید در تمامی حالات این خط از خط آبی که نشان‌دهنده مقدار واقعی یعنی $f*(n)$ است کمتر است در نتیجه می‌توان گفت این تابع قابل قبول است.
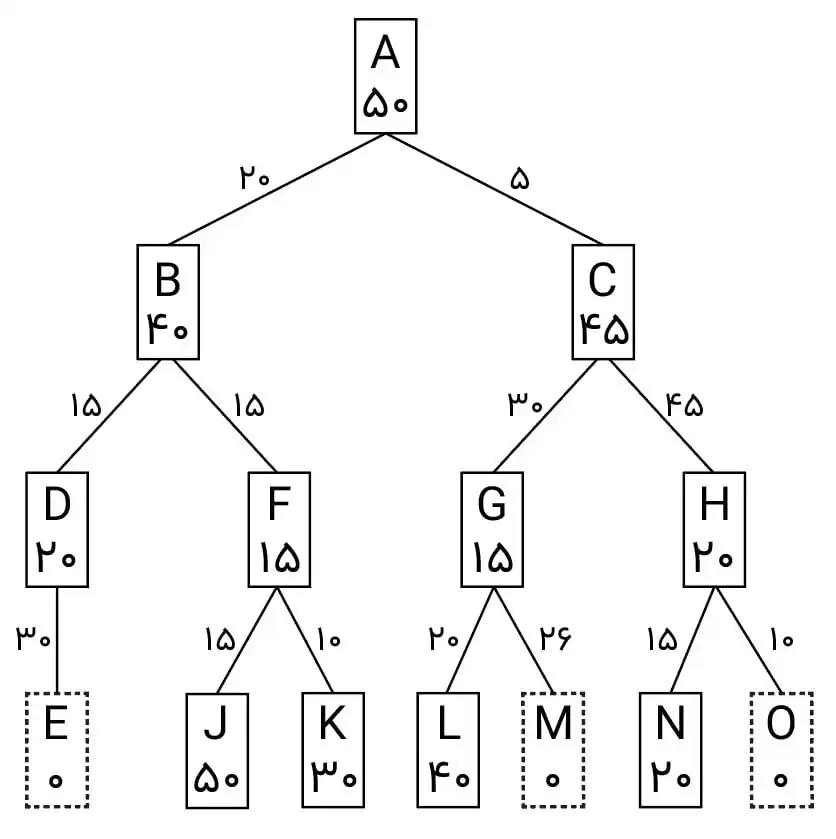
دشوار درخت جستجوی زیر داده شده است. گره A، وضعیت اولیه می‌باشد. وضعیت‌های جواب نیز با مربع‌های نقطه‌چین نشان شده‌اند. اعداد روی یال‌ها هزینه استفاده از آن مسیر (یال) را نشان میدهد. اعداد داخل هر گره نیز تخمین فاصله تا هدف را مشخص میکند. اگر برای جستجو از روش \( {IDA}^* \) استفاده شود، میزان حد آستانه که جهت انتخاب گره‌ها، هنگام ورود به صف در نظر گرفته میشود پس از گرفتن مقدار اولیه، چندبار تغییر میکند؟ الگوریتم های جستجوی آگاهانه
گزینه 3 صحیح است.
یادآوری روش IDA* و نکات مربوط به آن :
روش IDA* روشی مشابه A* است که در جهت بهبود وضعیت مرتبه حافظه A* ارائه شده است و از ایده جستجو عمقی تکرار شونده استفاده میکند. پس مصرف حافظه این روش نسبتا خوب است و از آن‌جا که برمبنای A* و جستجو عمقی تکرار شونده است کامل نیز می‌باشد و کارایی خوبی دارد چرا که مرتبه زمانی آن مشابه A* است. در این روش درخت جستجو به صورت تکراری از ریشه تا زمانی که مقدار تمام گره ها از cutoff بیشتر شود به صورت عمقی ساخته میشود (به عبارتی همه گره هایی که f(n) آنها از cutoff کمتر است به صورت پیش ترتیب بررسی می‌شوند). سپس در هر تکرار مقدار cutoff به کوچکترین مقدار f(n) گره های موجود در گراف بروزرسانی میشود تا جایی که به هدف برسیم. این روش از آن‌جا که در هر مرحله کل درخت جستجو از ابتدا می‌سازد، دوباره کاری دارد که یکی از نقطه ضعف های آن محسوب میشود.
در مرحله اول cutoff = 50 در نظر گرفته میشود و درخت زیر بدست می‌آید:
در مرحله بعدی cutoff به کمترین مقدار f(n) یعنی ۶۰ تنظیم میشود :
از آنجایی که هنوز به هدف نرسیدم بازهم الگوریتم را ادامه می‌دهیم و در مرحله بعدی cutoff به کمترین مقدار f(n) یعنی ۶۱ تنظیم میشود و در این مرحله گره M بسط داده شده و به هدف می‌رسیم. پس به جز تنظیم اولیه cutoff به مقدار 50 ، دوبار مقدار cutoff تغییر کرد و جواب گزینه سوم می‌باشد.
متوسط در مسئله حرکت در یک راه پیچ در پیچ (maze) فرض کنید اعمال بتواند در یک جدول \(n\times m\) که بعضی از خانه‌ها سیاه (غیر قابل عبور) است به چهار جهت افقی و عمودی (و نه قطری) حرکت کند. در این مسئله برای یافتن کوتاه‌ترین مسیر کدام یک از جملات زیر صحیح نیست؟ الگوریتم های جستجوی آگاهانه
در این مسئله باید به این نکته توجه داشته باشیم که هزینه تمام حرکات یکسان است همچنین قابل قبول بودن یا سازگار بودن تابع هیوریستیک استفاده شده در جستجوی $A^\ast$ مشخص نشده است.
گزینه ۱ : در الگوریتم $A^\ast$ در صورتی که h قابل قبول باشد جواب بهینه یافت میشود. هم چنین درصورتی که h سازگار باشد آنگاه هیچ الگوریتم دیگری غیر از $A^\ast$ وجود ندارد که از h استفاده کند و تعداد گره کمتری نسبت به $A^\ast$ بسط دهد به عبارت دیگر در این حالت الگوریتم $A^\ast$ کارآمد بهینه است. الگورتیم BFS نیز در صورتی که هزینه تمام حرکات یکسان باشد، بهینه است. با فرض اینکه الگوریتم $A^\ast$ یک الگورتیم کارآمد بهینه است (تابع هیوریستیک آن سازگار است) نسبت به هر الگوریتم بهینه مانند BFS در حالت یکسان بودن هزینه حرکات ، سریعتر جواب را پیدا میکند و به عبارتی تعداد گره‌هایی که بسط میدهد کمتر مساوی BFS و این گزینه را می‌توان درست در نظر گرفت.
گزینه ۲ : جستجو عمق اول یک روش جستجو ناآگاهانه است که نه بهینه است و نه کامل (فقط در صورت متناهی بودن فضای مسئله (عمق مسئله) و جستجو به صورت گرافی کامل است ) برای مثال در صورتی که از این الگوریتم در حالت درختی استفاده کنیم می‌تواند در حلقه بینهایت گیر کند و هیچگاه به جواب نرسد در این صورت می‌توان گفت که این گزینه که می‌گوید جستجوی $A^\ast$ تعداد گره کمتری نسبت به جستجوی عمق اول بسط میدهد می‌تواند درست باشد اما در حالت های دیگر مثل جستجو گرافی یا سازگار نبودن تابع هیوریستیک $A^\ast$ لزوما این شرط برقرار نیست و امکان اینکه جستجو عمق اول زودتر از $A^\ast$ به جواب برسد وجود دارد. در کل فعلا این گزینه را درست فرض می‌کنیم تا ببینم گزینه دیگری که در همه حالات غلط باشد داریم یا نه !
در اینجا خوب است که بخشی از یکی از تمرین‌های راسل که مرتبط با این سوال است یادآوری شود.
3.14 Which of the following are true and which are false? Explain your answers.
a. Depth-first search always expands at least as many nodes as A* search with an admissi-
ble heuristic. (false)
گزینه ۳ : همان طور که در گزینه ۲ اشاره شد جستجو عمق اول یک روش جستجو ناآگاهانه است که نه بهینه و نه کامل (فقط در صورت متناهی بودن فضای مسئله (عمق مسئله) و جستجو به صورت گرافی کامل است ) با این فرض این گزینه را در دو حالت جستجو درختی و گرافی بررسی می‌کنیم. در حالت جستجو درختی DFS می‌تواند در حلقه بینهایت گیر کند و هیچگاه به جواب نرسد، در این حالت BFS با هزینه حرکات یکسان بهنیه و کامل است و زودتر از DFS نیز به جواب می‌رسد. در حالت گرافی با فرض متناهی بودن مسئله نیز هر دو به جواب می‌رسند اما ممکن است با توجه به عمق و مکان هدف هر کدام سریعتر به جواب برسند. در بدترین حالت DFS برای پیدا کردن هدف تمام خانه ها را یکبار بررسی میکند اما BFS فقط فضای مسئله را تا عمقی که هدف در آن قرار دارد بررسی میکند. اگر بدترین حالت را در نظر بگیریم با اغماض می‌توان گفت در حالت جستجو گرافی نیز BFS سریعتر است و این گزینه در هر دو حالت غلط میشود.
گزینه ۴ : جستجو BFS در حالتی که هزینه تمام حرکات یکسان است، بهینه و کامل است و بهترین جواب را پیدا میکند در صورتی که جستجو DFS تضمینی برای یافتن جواب بهینه یا حتی پیدا کردن جواب ندارد پس این گزینه درست است.
توضیحات این سوال ناقض و غیر استاندارد است و سعی کردیم هر گزینه را با در نظر گرفتن فرضیات مختلف توضیح دهیم و بطورکلی سوال خیلی استاندارد نیست.
متوسط کدام یک از گزینه‌های زیر غلط است؟ الگوریتم های جستجوی آگاهانه
پاسخ گزینه 1 است.
یادآوری :
ابتدا به توضیح برخی از الگورتیمها می‌پردازیم:
الگوریتم شبیه‌سازی ذوب شده:
الگوریتم شبیه‌سازی ذوب شده در واقع ترکیب تپه‌نوردی و قدم‌برداری تصادفی است. پایه اصلی این الگوریتم استفاده از مفهوم دما است به این معنی که هر چه دما بالاتر باشد احتمال رفتن به گره بدتر از گره جاری بیشتر میشود و هر چه دما پایین‌تر باشد این احتمال کاهش می‌یابد.
در این الگوریتم در هر مرحله پارامتر دما (T) تنظیم میشود و در صورتی که دما به صفر برسد گره جاری به عنوان جواب نهایی برگردانده میشود. در مرحله بعد یک گره تصادفی از همسایه‌های گره جاری انتخاب میشود و اختلاف ارزش گره انتخابی با گره جاری سنجیده میشود($\Delta E$). چنانچه ارزش گره انتخابی بیشتر از گره جاری باشد به گره انتخابی رفته و مراحل را دوباره تکرار می‌کنیم اما اگر گره جاری ارزش کمتری داشته باشد با احتمال $\frac{1}{e^{\frac{\Delta E}{T}}}$ به گره انتخابی می‌رویم و مراحل را دوباره تکرار می‌کنیم و در غیر اینصورت یک گره دیگر را به صورت تصادفی انتخاب می‌کنیم.
الگوریتم پرتو محلی:
الگوریتم پرتو محلی به این صورت است که در ابتدا k گره تصادفی برای شروع انتخاب می‌شوند. سپس از میان همه گره‌های همسایه این k گره، k تا از بهترین همسایه‌ها را انتخاب می‌کنیم. (در صورتی که هر یک از گره‌های همسایه تولید شده هدف باشد کار تمام است در غیر اینصورت الگوریتم را ادامه می‌دهیم).
الگوریتم hill climbing :
در الگوریتم hill climbing یک گره به صورت تصادفی بعنوان حالت شروع انتخاب میشود و از بین همسایه‌های این گره بهترین آن انتخاب میشود و در صورتی که گره همسایه انتخابی ارزش بیشتری نسبت به گره جاری داشته باشد به آن می‌رود.
اعمال اصلی در الگوریتم ژنتیک عبارت است از :
- ترکیب (cross over) : ترکیب دو کروموزوم و تولید دو کروموزوم جدید
- جهش (mutation) : تغییر حداقل یک ژن از کروموزوم و تولید یک کروموزوم جدید
- انتخاب (selection) : انتخاب k کروموزوم بر اساس احتمال انتخاب آنها
گزینه ۱ : این گزینه نادرست است چرا که الگوریتم شبیه‌سازی حرارت با احتمال نزدیک به یک، به جواب بهینه سراسری می‌رسد نه دقیقا یک پس ممکن است نتواند از بهینه محلی فرار کند.
گزینه ۲ : این گزینه را به 2 صورت می‌توان تفسیر کرد:
1- هر وقت تپه نوردی را اجرا کنیم حتما در بهینه محلی گیر میکند.این گزاره غلط است و تپه نوردی می‌تواند به بهینه سراسری همگرا شود.
2-اگر الگوریتم تپه نوردی در بهینه محلی گرفتار شد،همان جا گیر میکند و نمی‌تواند از آن خارج شود.این گزاره درست است.
احتمالا منظور طراح،حالت دوم تفسیر این گزینه بوده است و به همین دلیل گزینه 1 در کلید سنجش به عنوان پاسخ اعلام شده است.ولی با این نوع نوشتار می‌توان این گزاره را هم غلط فرض کرد.
گزینه ۳ : این گزینه نیز درست است چرا که بسته به نقاط شروع امکان اینکه به بهینه سراسری نیز برسیم وجود دارد.
گزینه ۴ : درست است چرا که این الگورتیم از اعمال mutation و cross over برای ایجاد نسل جدید استفاده میکند و این امر امکان فرار از بهینه محلی را برای آن فراهم میکند.
دشوار در محیطی به شکل زیر که مستطیل \(\mathrm{M\times N}\) است، بعضی از خانه‌ها (خانه‌های طوسی‌رنگ) مسدود است و در برخی از خانه‌ها غذا وجود دارد. فرض کنید عامل از یک نقطه S شروع میکند و هدفش این است که خانه‌های حاوی غذا را ملاقات کند. در هر کنش، عامل می‌تواند در هر کدام از راستاهای بالا، پایین، چپ و راست تا جایی که به مانعی نرسیده به تعداد دلخواه حرکت کند. چنانچه مقصد عامل خانه‌ای باشد که در آن غذا وجود دارد، آن غذا ملاقات‌شده به حساب می‌آید. لازم به ذکر است که هر کنش عامل، مستقل از تعداد خانه‌ای که از آنها عبور کرده، یک واحد هزینه دارد. در این خصوص کدام گزینه نادرست است؟ الگوریتم های جستجوی آگاهانه
| غذا | ||||
| S | غذا |
گزینه 4 صحیح است.
گزینه ۱ : درست است در واقع تعداد حالاتی که در هر خانه عامل می‌تواند انجام دهد این است که در یکی از راستاها حرکت را انجام دهد و در هر خانه‌ای از آن راستا که دوست دارد متوقف شود به اینصورت می‌توان به فاکتور انشعاب M+ N -2 که از M+N کوچکتر است رسید.
گزینه ۲ : این گزینه درست است چرا که در این مسئله هزینه حرکات یکسان و مثبت است و در این حالت می‌توان گفت که BFS می‌تواند جواب بهینه را پیدا کند.
گزینه ۳ : این گزینه درست است چرا که برای دریافت هر غذا حداقل به یک حرکت نیاز داریم و می‌توان گفت در هر مرحله تعداد حرکات واقعی برای رسیدن به هدف از تعداد غذاها بیشتر مساوی است پس تابع ابتکاری تعداد غذاهای ملاقات نشده قابل قبول است.
گزینه ۴ : این گزینه نادرست است چرا که در این سوال عامل می‌توان با یک حرکت که هزینه واحد دارد چند خانه را که به صورت متوالی و در یک راستا هستند طی کند پس در این حالت دیگر مجموع فواصل منهتن را نمی‌توان تابعی قابل قبول برای این مسئله در نظر گرفت (حتی اگر هزینه هر حرکت برابر با تعداد خانه‌های طی شده در آن حرکت بود چون در گزینه 4 گفته شده تابع ابتکاری برابر مجموع فواصل منهتن عامل تا همه خانه‌های حاوی غذاهای ملاقات نشده است این تابع قابل قبول نمی‌شد)
متوسط در الگوریتم ژنتیک برای جستجو، مقدار شایستگی (fitness) برای یک جمعیت با اندازه 5، به صورت 3 ،5 ،3 ،4 و 5 است. پس از انجام عملیات انتخاب (selection) به چه احتمالی عضو اول جمعیت که شایستگی آن 4 است، حداقل یکبار انتخاب خواهد شد؟ الگوریتم های جستجوی آگاهانه
گزینه 3 صحیح است. در الگوریتم ژنتیک انتخاب نسل بعدی به این صورت است که احتمال انتخاب یک عضو برای مرحله بعدی متناسب با شایستگی آن است. برای بدست آوردن احتمال خواسته شده در صورت سوال بهتر است از متمم آن استفاده کنیم یعنی در مرحله اول احتمال اینکه عضو اول جمعیت اصلا انتخاب نشود را به‌دست بیاوریم.
مجموع شایستگی‌ها = 20
احتمال انتخاب عضو اول = $\frac{4}{20}$
احتمال عدم انتخاب عضو اول در هیچکدام از ۵ مرحله انتخاب نسل بعدی: $ \frac{16}{20}\times \frac{16}{20}\times \frac{16}{20}\times \frac{16}{20}\times \frac{16}{20}={(\frac{4}{5})}^5\ $
احتمال اینکه عضو اول حداقل یکبار انتخاب شود : $1-{\left(\frac{4}{5}\right)}^5=1-\ {0.8}^5$
توضیح اضافه مجدد: در الگوریتم ژنتیک هرچه مقدار تابع شایستگی عضوی بیشتر باشد احتمال انتخاب آن بیشتر است.
در اینجا ۵ عضو داریم که مقدار تابع شایستگی آن به ما داده شده است.
احتمال اینکه عضو با مقدار ۴ در یک انتخاب، انتخاب نشود برابر است با:
$\frac{3+5+3+5}{3+5+3+5+4}=\frac{16}{20}=0.8$
در اینجا ۵ عضو داریم که مقدار تابع شایستگی آن به ما داده شده است.
احتمال اینکه عضو با مقدار ۴ در یک انتخاب، انتخاب نشود برابر است با:
$\frac{3+5+3+5}{3+5+3+5+4}=\frac{16}{20}=0.8$
چون جمعیت ۵ است در هر انتخاب ۵ عضو انتخاب میشود احتمال اینکه هیچکدام عضو با مقدار ۴ نباشد برابر است:
${0.8}^5$
${0.8}^5$
احتمال اینکه عضو ۴ حداقل یکبار انتخاب شود برابر است با:
$P(All\ possibilities)-P\left(not\ choosing\ 4\right)=1-{0.8}^5$
$P(All\ possibilities)-P\left(not\ choosing\ 4\right)=1-{0.8}^5$
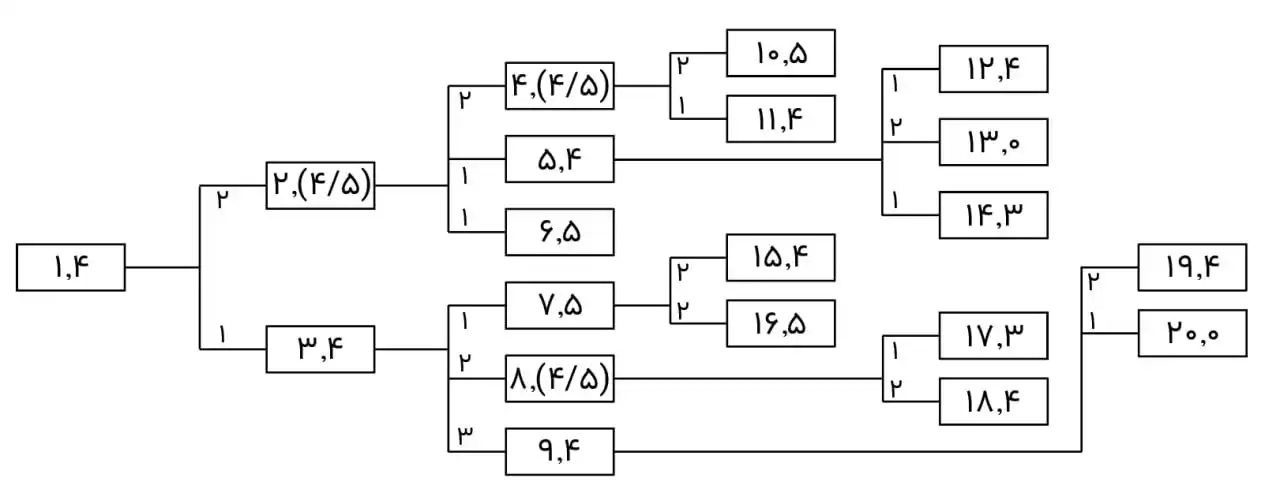
متوسط در درخت تصمیم‌گیری زیر با استفاده از جستجوی $A^*$ کدام گزینه شماره گره‌های مورد بررسی را مشخص میکند؟ توجه کنید که هزینه هر گره در کنار شماره آن و هزینه هر شاخه روی آن نوشته شده است. (در هر گره اولین عدد شماره گره و دومین عدد هزینه می‌باشد.) الگوریتم های جستجوی آگاهانه
در جست‌وجوی A* اولویت جست‌وجو با گره‌ای است که مجموع هزینه کمترین مسیر طی شده تا آن گره و هزینه تخمین زده تا گره هدف برای آن کمترین باشد، این مجموع را برای گره i با $f_i$ نشان می‌دهیم.
اگر تابع heuristic در اینجا admissible بود (فاصله تخمین زده از فاصله واقعی بیشتر نباشد.) می‌توانستیم به راحتی با پیدا کردن f گره‌هایی که مقدارشان کمتر از فاصله رسیدن تا گره بهینه است جواب را بیابیم. اما در اینجا چنین چیزی برقرار نیست (چرا؟) بنابراین چاره‌ای نداریم جزء اینکه براساس الگوریتم جلو رفته و گره‌های مشاهده شده را بدست آوریم.
در ابتدا گره ۱ جست‌وجو میشود.
$f_2=2+4.5=6.5,\ f_3=1+4=5$
تا الان کوچکترین ۳ است بنابراین گره ۳ جست‌وجو میشود. (با جست‌وجوی ۳، سه گره زیر دیده می‌شوند.)
$f_7=1+1+5=7,\ $
$f_8=1+2+4.5=7.5,$
$f_9=1+3+4=8$
پس از آن گره ۲ جست‌وجو میشود. (به مقادیر f دقت کنید همیشه کوچکترین انتخاب میشود.)
$f_4=2+2+4.5=8.5,$
$f_5=2+1+4=7$
$f_6=2+1+5=8$
پس از گره ۲ دو گره ۵ و ۷ بیشترین اولویت را دارند، فرض کنید ابتدا گره ۵ جست‌وجو میشود. با اینکار ۳ گره زیر دیده می‌شوند:
$f_{12}=2+1+1+4=8$
$f_{13}=2+1+2=5$
$f_{14}=2+1+1$
گره بعدی برای جست‌وجو دیگر ۷ نیست بلکه گره ۱۳ است که گره هدف می‌باشد و جست‌وجو به پایان می‌رسد.
کل گره‌های بررسی شده تا زمان یافتن گره هدف: (گره‌هایی که f آنها حساب شد)
$1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9,\ 12,\ 13,\ 14$
بنابراین جواب صحیح گزینه ۴ می‌باشد.
توجه: حال فرض کنید در بالا به جای اینکه ابتدا ۵ چک شود گره ۷ جست‌وجو شود. با اینکار ۲ گره زیر دیده می‌شوند:
$f_{15}=1+1+2+4=8$
$f_{16}=1+1+2+5=9$
با توجه به این اعداد اولویت بعدی همان گره ۵ می‌باشد. که مشابه بالا پیش رفته و به گره هدف ۱۳ می‌رسد.
اگر گره ۷ زودتر از ۵ جست‌وجو می‌شد باید گزینه‌ای با مشاهدات زیر در سؤال می‌بود:
$1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9,\ 12,\ 13,\ 14,\ 15,\ 16$
اما در اینجا نیست بنابراین گزینه صحیح همان گزینه ۴ است.
متوسط در مورد توابع heuristic کدام مورد نادرست است؟ الگوریتم های جستجوی آگاهانه
گزینه 2 جواب است. بررسی گزینه‌ها:
گزینه ۱:
توابع heuristic، توابعی مثبت هستند، بنابراین حاصل $|h_1-h_2|$ در تمام گره‌ها از حداقل یکی از دو تابع heuristic کمتر است. و چون می‌دانیم admissible بودن به معنای کوچکتر بودن تابع heuristic داده شده از مقدار واقعی فاصله هر گره تا گره هدف بهینه است و هر دو تابع داده شده admissible می‌باشند، عبارت داده شده هم admissible است.
به ازای هر گره n داریم:
$\left|h_1-h_2\right|<h_1\ or\ \left|h_1-h_2\right|<h_2\ \ \ \ and\ \ \ \ h_1\le h^*\ and\ h_2\le h^*$
$\to \left|h_1-h_2\right|\le h^*\to admissible$
این گزینه صحیح است.
گزینه ۲:
با یک مثال می‌توان نشان داد که عبارت داده شده نیز می‌تواند consistent باشد.
فرض کنید که $h_1=\frac{2}{3}\times h$، $h_2=\frac{1}{3}\times h$ و h یک تابع هیوریستیک consistent باشد. در این صورت مطمئنیم که $h_1$ و $h_2$ نیز consistent هستند. حال اگر حاصل عبارت بالا را حساب کنیم داریم:
${\mathrm{max} \left(h_1,h_2\right)\ }+{\mathrm{min} \left(h_1,\ h_2\right)\ }={\mathrm{max} \left(\frac{2}{3}\times h,\frac{1}{3}\times h\right)\ }+{\mathrm{min} \left(\frac{2}{3}\times h,\frac{1}{3}\times h\right)\ }=\frac{2}{3}h+\frac{1}{3}h=h$
بنابراین عبارت داده شده می‌تواند consistent باشد. این گزینه غلط است.
گزینه ۳:
Consistent بودن یک تابع heuristic باعث میشود که بهینه‌ترین جواب از لحاظ هزینه مسیر پیدا شود/ حال ممکن است این گره بهینه ممکن است در جایی باشد که برای رسیدن به آن باید از چند گره بگذریم درحالی که جواب غیربهینه در کنار ریشه باشد و تابع heuristic غیر consistent همان اول آن را پیدا کند و الگوریتم را به پایان برساند.
این گزینه صحیح است.
گزینه ۴:
توابع heuristic یک تخمین از فاصله گره فعلی تا نزدیکترین گره هدف می‌باشند. این توابع هرچه نزدیک‌تر به تابع heuristic اصلی (h*) باشند عملکرد بهتری دارند. همچنین می‌دانیم این توابع برای اینکه مجاز باشند باید از تابع heuristic اصلی (h*) کوچکتر باشند.
بنابراین تا زمانیکه این توابع از حالت مجاز خارج نشوند، مطلوب‌تر می‌باشد که مقادیرشان تا می‌تواند بزرگ باشد.
حال در این گزینه مشخص است که اگر یک تابع از دیگری بزرگتر باشد جواب max همان تابع میشود و تفاوتی برای ما ندارد. امّا اگر همانطور که در گزینه آمده در بعضی گره‌ها تابع دیگر هم بزرگتر باشد، تابع heuristic بزرگ‌تری نسبت به ۲ حالت قبل بدست می‌آوریم که مطلوب‌تر و مناسب‌تر است.
این گزینه صحیح است.
یادآوری:
برای آنکه جست‌وجوی $A^*$ بهینه باشد تابع مکاشفه در جست‌وجوی گرافی باید consistent و در جست‌وجوی درختی حداقل admissible باشد.
شرط admissible بودن:
$h(n)\le h^*(n)$
h(): تابع مکاشفه تعریف شده.
h*(): تابع مکاشفه واقعی یا به عبارتی تابع مکاشفه‌ای که هزینه واقعی بهینه از گره مورد نظر به هدف با میدهد.
شرط consistent بودن:
$h\left(n\right)\le c\left(n,\ a,\ n'\right)+h\left(n'\right)$
h(): تابع مکاشفه تعریف شده.
c(n, a, n’): فاصله واقعی رسیدن از گره n به n’ با انجام عمل a یا با طی یال a.
نمونه سوالات فصل بازی های رقابتی درس هوش مصنوعی
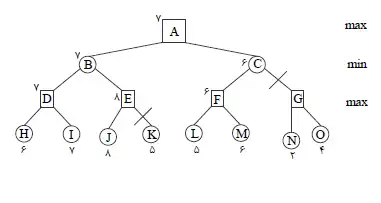
متوسط در جستجوی خصمانه با هرس آلفا – بتا، مقدار آلفا در حین جستجو در یک گره max برابر با 5 شده است. کدامیک از گزاره‌های زیر درست است؟ بازی های رقابتی
در کل هرس آلفا-بتا به صورت زیر رخ میدهد:
$\square$ - جست‌وجو در هر یک از فرزندان گره‌های max زمانی متوقف میشود که مقدار آن گره کمتر از مقدار فعلی گره max که با آلفا آن را حفظ می‌کنیم شود.
$\square$ - جست‌وجو در هر یک از فرزندان گره‌های min زمانی متوقف میشود که مقدار آن گره بیشتر از مقدار فعلی گره min که با بتا آن را حفظ می‌کنیم شود.
با توجه به این توضیحات مشخص است که گزینه ۱ صحیح است.
بررسی دقیق‌تر گزینه‌ها:
گزینه ۱:
گره‌های فرزند یک گره max، گره‌های min هستند و این گره‌ها هر گاه جوابی کمتر از مقدار آلفا (که در اینجا ۵ هست) گرفتند با ادامه جست‌وجو در آنها مقدارشان بیشتر نشده و حتی ممکن است کمتر شود، بنابراین جست‌وجو در آنها برای گره max فایده‌ای نداشته و بهترین کار توقف جست‌وجو در آن گره است (کاری که هرس آلفا-بتا انجام میدهد).
بنابراین این گزینه درست است.
گزینه ۲:
فرض کنید یکی از گره‌های min که فرزند گره max مورد نظر ما است مقداری بیشتر از ۵ گرفت و ما جست‌وجو را برای آن متوقف کردیم. حال گره max ما (اگر مقدار بیشتری نیابد) آن گره را برای هدف بعدی انتخاب میکند و مقدار خود را مقدار آن گره قرار میدهد، این در حالی است که ممکن است مقدار واقعی آن گره min (که از جست‌وجوی کامل آن بدست می‌آید.) کمتر از ۵ باشد. در آن صورت انتخاب ما غیر بهینه بوده و این خلاف بهینه بودن الگوریتم هرس آلفا-بتا است.
گزینه ۳ و ۴:
خیر مقادیر آلفا و بتا گره‌های زیرین به مقادیر بالایی آنها ربطی ندارد.
برای این دو گزینه می‌توان مثال نقض زیر را آورد: (به دو گره max که نوه‌های ریشه هستند دقت کنید اینجا ریشه ۱۰ است ولی دو نوه آن هم آلفا کوچکتر و هم بزرگتر دارند.)
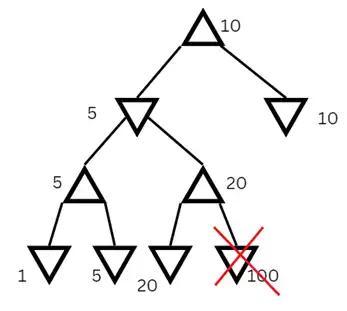
آسان با استفاد از روش هرس $\alpha-\beta$ کدامیک از گره‌های درخت زیر جست‌وجو نخواهد شد؟ بازی های رقابتی
در اینجا با هرس G، O و N نیز هرس میشود.
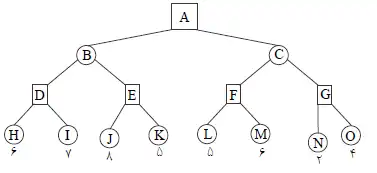
دشوار فرض کنید در درخت زیر، مقادیر گره‌های برگ متمایز هستند. احتمال اینکه گره f هرس نشود چقدر است؟ بازی های رقابتی
در صورتی که $min(a,b)$ از $min(c,d,e)$ کوچکتر باشد، f هرس نمی‌شود. یعنی اگر $min(a,b,c,d,e)$ برابر a يا b باشد، f هرس نمی‌شود. احتمال اینکه هریک از اعداد a یا b از چهار عدد دیگر کمتر باشد ۲۰ درصد است. در نتیجه احتمال هرس نشدن f برابر ۴۰ درصد خواهد بود.
نحوه محاسبه احتمال اینکه a کوچکترین باشد (برای b نیز به همین صورت است):
۵ عدد داریم تعداد کل ترتیب‌هایی که برای دنباله مرتب شده این عدد‌ها وجود دارد برابر !5 است.
تعداد کل ترتیب‌هایی که برای دنباله مرتب شده این عدد‌ها وجود دارد که عدد a کوچکترین باشد برابر !۴ است.
بنابراین احتمال اینکه a کوچکترین باشد برابر است با:
$\frac{4!}{5!}=\frac{1}{5}=20\%$
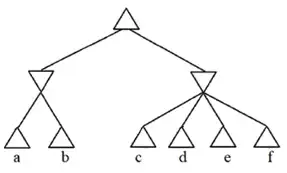
دشوار اگر در یک بازی دو طرفه با عنصر شانس، هر بازیکن در هر گام 3 انتخاب داشته باشد و عنصر شانس برای هر بازیکن 2 حالت را ایجاد کرده و هر بازیکن دقیقاً n حرکت انجام دهد، تعداد برگ‌های (پایانه‌های) این درخت بازی از چه مرتبه‌ای است؟ بازی های رقابتی
بعد از هر گره min یا max یک گره شانس خواهیم داشت. در نتیجه اگر هر بازیکن n حرکت انجام دهد، در مسیر ریشه تا برگ، n گره min و n گره max خواهیم داشت. تعداد گره‌های شانس نیز 2n خواهد بود. با توجه به این که تعداد فرزندان گره‌های min و max برابر 3 و تعداد فرزندان گره‌های شانس برابر 2 است، تعداد برگ‌های درخت از مرتبه $\mathrm{O}\left(\mathrm{2}^{\mathrm{2n}}\times\mathrm{3}^{\mathrm{2n}}\right)=\mathrm{O}\left({\mathrm{36}}^\mathrm{n}\right)$ خواهد بود.
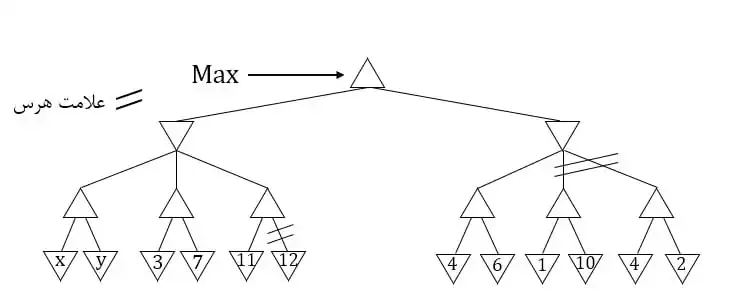
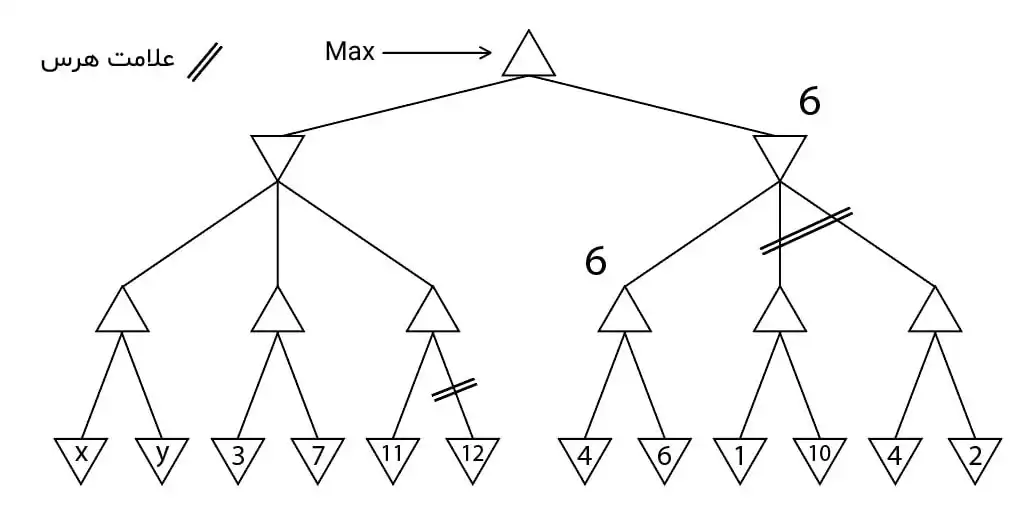
دشوار در درخت بازی زیر کدام یک از گزینه‌ها محدوده مناسبی برای مقادیر مثبت x و y تعیین میکند به‌طوری که شاخه‌های علامت‌زده شده در هرس آلفا_بتا، هرس شوند؟ بازی های رقابتی
گزینه 4 صحیح است.
برای حل این سوال باید الگوریتم آلفا و بتا را روی درخت اجرا کنیم و در حالت‌هایی که هرس رخ داده است از عبارت شرط هرس جهت تعیین محدود مقادیر x, y استفاده کنیم.
در ابتدای کار چون نمی‌دانیم که کدامیک از مقادیر x,y بزرگتر است برای مقدار آلفا متناظر با شاخه سمت چپ max(x,y) را در نظر می‌گیریم. مقدار بتا گره پدر آن را نیز با این مقدار جایگذاری می‌کنیم. پس از آن به شاخه بعدی می‌رویم و در مرحله ابتدایی آلفا برابر با ۳ میشود. در اینجا شرط هرس برای هرس گره ۷ برقرار نشده است پس 3<max(x,y) بوده است. پس از بررسی شاخه ۷ مقدار آلفا پدر آن برابر با ۷ میشود. از طرفی چون نمی‌دانیم کدام یک از مقادیر 7 یا max(x,y) کوچکتر است که آن را بعنوان بتا پدرشان انتخاب کنیم از min آنها استفاده می‌کنیم. در مرحله بعد پس از بررسی گره ۱۱ شرط هرس برقرار شده است چرا که گره ۱۲ حذف شده است. پس می‌توان نتیجه گرفت که $11 \ge min (7,max(x,y))$ است. در مرحله بعدی بتا گره min همان $min(7, max(x,y))$ می‌ماند چرا که ۱۱ از ۷ کوچکتر است. در مرحله بعد همین مقدار را برای آلفا ریشه در نظرگرفته و به بررسی زیر شاخه سمت راست ریشه می‌پردازیم.
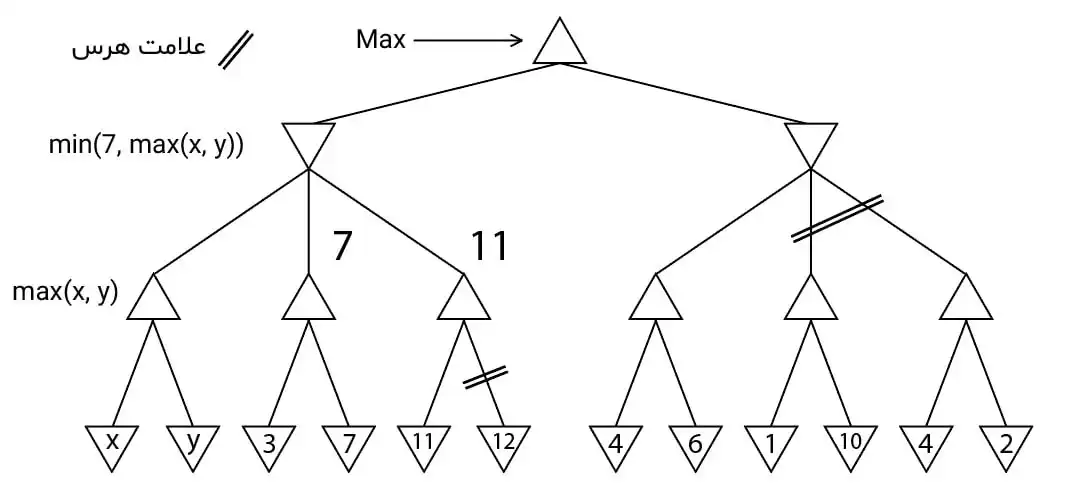
در سمت راست پس از بررسی زیر شاخه اول مقدار ۶ بعنوان آلفا گره max تنظیم میشود. در این مرحله با توجه به اینکه هر دو زیر درخت سمت راست هرس شده‌اند پس شرط هرس برقرار شده بوده است یعنی $6 \le min (7,max(x,y))$ و در کل باتوجه به بازه‌های بدست آمده باید گزینه مناسب را انتخاب کنیم.
$6 \le min(7,max(x,y)) \le 11 \\ \ \ \ \ \ \ \ \ \ max(x,y) \gt 3$
$x \ge 6 \ \text{یا }\ y \ge 6$
که با توجه به عبارت بالا فقط گزینه ۴ که $y \gt 7$ منطبق بر بازه بالا است و می‌تواند پاسخ سوال باشد.
دشوار در مورد بازی دو نفره صفر جمع (Zero - Sum) اگر بخواهیم از الگوریتم Minimax استفاده کنیم تا حرکت بهینه را برای بازیکن مورد نظر پیدا کنیم، کدام مورد درست نیست؟ بازی های رقابتی
گزینه 4 صحیح است.
گزینه ۱ : درست است چرا که در این صورت ترتیب و بزرگ یا کوچکتر بودن سودمندی گره‌ها نسبت به یکدیگر تغییری نمی‌کند.
گزینه ۲ : این گزینه نیز درست است چرا که بطور کلی روش جستجو minimax به دنبال حداکثر کردن حداقل سودمندی است و این حداقل سودمندی زمانی که بازیکن حریف بهینه عمل کند حاصل میشود.
گزینه ۳ : این گزینه نیز درست است.
گزینه ۴ : این گزینه نادرست است چرا که بطور کلی روش جستجو minimax به دنبال حداکثر کردن حداقل سودمندی است و امکان ندارد در مقابل هیچ حریفی (مثلا حریف غیر بهینه) سودمندی کمتر از سودمندی بدست آمده در مقابل حریف بهینه بدست آید.
نمونه سوالات فصل ارضای محدودیت درس هوش مصنوعی
متوسط مسئله ارضای قیود زیر را در نظر بگیرید. فرض کنید D، C، B، A و E متغیرهای مسئله باشند. دامنه هر متغیر عددی صحیح بین ۱ تا ۶ است. فرض کنید پاسخی که تا الان ساخته شده است، به صورت $\{A=1,B=2 \}$ باشد. در گام بعد، کدام متغیر بررسی میشود؟ مسائل ارضای محدودیت
$A+B \ge 3$
$B-C \le 0$
$B+D \ge 4$
$D-E-C \le 0$
$E+C \ge 2$
در حل مسئله ارضای قیود اولویت انتخاب متغیر با متغیری است که کوچکترین دامنه سازگار را دارد، زیرا این متغیر بیشترین محدودیت را ایجاد میکند و هزینه جست‌وجو در مراحل بعدی را کاهش میدهد. به این متغیر اصطلاحات MRV (Minimum Remaining Values) و MCV (Most Constrained Variable) نسبت داده میشود.
با توجه به اینکه A=1, B=2 است و دامنه از ۱ تا ۶ است باید بررسی کنیم کدام متغیر کمترین دامنه مورد قبول را دارد:
$B-C\le 0\to 2-C\le 0\to C\ge 2,$
$B+D\ge 4\to 2+D\ge 4\to D\ge 2,$
$D-E-C\le 0\to D\le E+C,$
$E+C\ge 2\to E\ge 2-C$
شرط آخر با توجه به شرط اول که $C \ge 2$ را نتیجه داد همیشه درست است. بنابراین این شرط محدودیتی برای حذف دامنه هیچ یک از دو متغیر ایجاد نمی‌کند.
شرط سوم چون E می‌تواند بدون هیچ مشکلی عدد ۶ را بگیرد و D حداکثر برابر ۶ میشود هیچ محدودیتی را ایجاد نمی‌کند.
بنابرای در نهایت دامنه سازگار متغیرها به شرح زیر است:
$C=\left\{2,\ 3,\ 4,\ 5,\ 6\right\},\ D=\left\{2,\ 3,\ 4,\ 5,\ 6\right\},\ E=\{1,\ 2,\ 3,\ 4,\ 5,\ 6\}$
وقتی دامنه متغیرها یکسان میشود باید متغیری را انتخاب کنیم که در تعداد بیشتری از شرایط با متغیرهای تعیین نشده قرار دارد یا به عبارتی درجه بیشتری در درخت CSP دارد. (degree heuristic)
در اینجا C در ۲ شرط حضور دارد در حالیکه D در ۱ شرط، بنابراین اولویت با C است و گزینه صحیح 1 است.
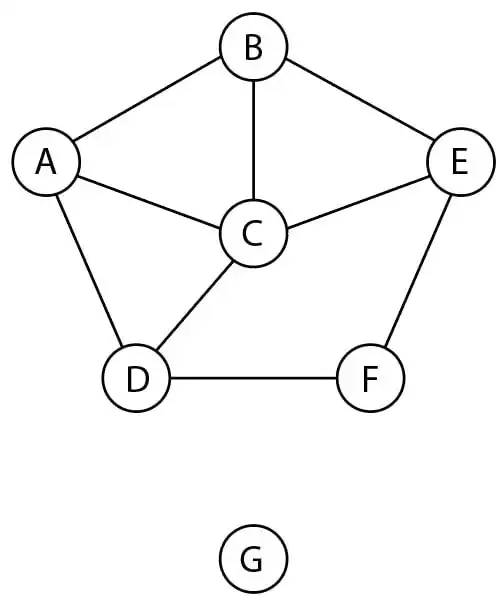
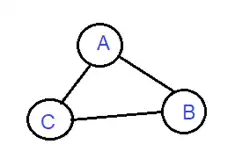
آسان در یک مسئله می‌خواهیم نقشه را با سه رنگ (R)Red، (G)Green و Blue (B) رنگ‌آمیزی کنیم طوری که هیچ دو کشوری که با هم مرز مشترک دارند هم‌رنگ نشوند. اطلاعات نقشه را به‌صورت گراف محدودیت زیر نمایش داده‌ایم (وجود لبه بین دو گره نشانه وجود مرز مشترک بین دو کشور مربوط به گره‌هاست.) بر اساس هیوریستیک‌های عمده مسائل CSP کدام گزینه زیر ترتیب بهتری برای دو کشوری که اول انتخاب می‌شوند است؟ مسائل ارضای محدودیت
گزینه 1 صحیح است.
از جمله هیوریستیک‌هایی که برای مسائل CPS بکار می‌روند می‌توان به MRV (انتخاب متغیری از بین متغیرهای بدون مقدار که کمترین دامنه مجاز را دارد) و Degree (متغیری که درجه بیشتری دارد و بیشترین محدودیت را به متغیرهای مقداردهی نشده اعمال میکند) اشاره کرد که MRV بر Degree الویت دارد. در گراف داده شده نیز از آنجایی که برای انتخاب اولین گره همه گره‌ها هر رنگی می‌توانند داشته باشند، MRV به هیچ گره‌ای الویت نمی‌دهد و پس از آن گره C با استفاده از هیوریستیک Degree انتخاب میشود پس از انتخاب C و انتساب یک رنگ به آن، از دامنه هر کدام از گره‌های A, B, E, D یک حالت کم میشود. در مرحله بعد برای انتخاب گره، MRV یکی از گره‌های A, B, E, D که حالت‌های مجاز کمتری نسبت به بقیه دارند را پیشنهاد میدهد که از بین این گره‌ها Degree نیز چون هر کدام از آنها دو محدودیت را به متغیرهای مقداردهی نشده اعمال میکند یکی را به تصادف انتخاب میکند و پاسخ گزینه ۱ میشود.
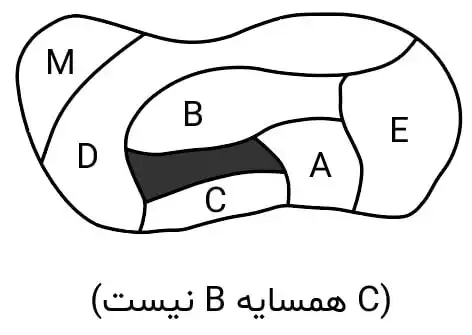
دشوار در یک مسئله رنگ‌آمیزی نقشه به شکل مقابل می‌خواهیم هیچ دو کشور همسایه‌ای هم‌رنگ نباشند و کشورهای E ،D ،C ،B ،A و M به یکی از سه رنگ قرمز، سبز و آبی رنگ شوند. فرض کنید در میانه یک جستجوی ارضای محدودیت (CSP) برای این مسئله، به کشور A رنگ قرمز و به کشور C رنگ آبی را نسبت داده باشیم. حال اگر بخواهیم به کشور M رنگ قرمز را نسبت دهیم، کدام تست زیر بروز تناقض و نیاز به عقبگرد را پیش‌بینی میکند؟ مسائل ارضای محدودیت
گزینه 2 صحیح است.
گزینه ۱: در این روش با هر مقداردهی به متغیرها دامنه مقادیر همه متغیرهای بدون مقدار که دارای محدودیت با متغیر مقداردهی شده می‌باشند بررسی و بروزرسانی می‌شوند. در این حالت در صورتی‌که به دامنه تهی برای یکی از متغیرها برسیم ناسازگاری رخ داده و عقبگرد می‌کنیم. جدول زیر اجرای این روش را نشان میدهد که همانطور که می‌بینیم هیچ دامنه تهی ای تا به این‌جای کار بدست نیامده است.
| A | B | C | D | M | E | |
| Initial domains | $R \ \ G\ \ B$ | $R \ \ G\ \ B$ | $R \ \ G\ \ B$ | $R \ \ G\ \ B$ | $R \ \ G\ \ B$ | $R \ \ G\ \ B$ |
| After A =red |
$R $
|
$ \ \ \ G\ \ B$ | $ \ \ \ G\ \ B$ | $R \ \ G\ \ B$ | $R \ \ G\ \ B$ | $ \ \ \ G\ \ B$ |
| After C =blue |
$R $
|
$ \ \ \ G\ \ B$ |
$B $
|
$R \ \ G\ \ $ | $R \ \ G\ \ B$ | $ \ \ \ G\ \ B$ |
| After M =red |
$R $
|
$ \ \ \ G\ \ B$ |
$B $
|
$ \ G\ \ $ |
$R $
|
$ \ \ \ G\ \ B$ |
گزینه ۲: سازگاری مسیر به این معنی است که اگر برای دو متغیر مقدار مجاز و معتبر وجود داشته باشد برای متغیر سوم نیز حداقل یک مقدار مجاز و معتبر وجود دارد پس اگر در گراف به ازای هر سه متغیر نکته بالا برقرار باشد می‌توان گفت سازگاری مسیر داریم. در گراف محدودیت حاصل از این مسئله پس از مقداردهی به گره‌های A و C و M مطابق صورت سوال دامنه‌های هر سه متغیر B, E, D به‌صورت {B, G} میشود که در این حالت می‌بینیم که سازگاری مسیر وجود ندارد و توانستیم با استفاده از این روش تناقض در مسئله را پیدا کنیم .(در این حالت از آنجایی که سه متغیر B, E, D به صورت مثلث بهم وابسته‌اند هرگونه مقداردهی به دو تا از آنها باعث تهی شدن دامنه سومی و در نتیجه ناسازگاری مسیر میشود)
گزینه ۳: این گزینه که به سازگاری نود اشاره میکند و محدودیت‌هایی یکانی را بررسی میکند به این معنی است که آیا بدون توجه به سایر نودها مقداری وجود دارد که به هر نود نسبت دهیم. در این تست در دامنه‌ی هر یک از گره‌ها حداقل یکی از مقادیر RGB وجود دارد و این تست کمکی به یافتن تناقض نمی‌کند.
گزینه ۴: این گزینه نادرست است چرا‌که دیدیم با استفاده از path consistency می‌توان تناقض را یافت.
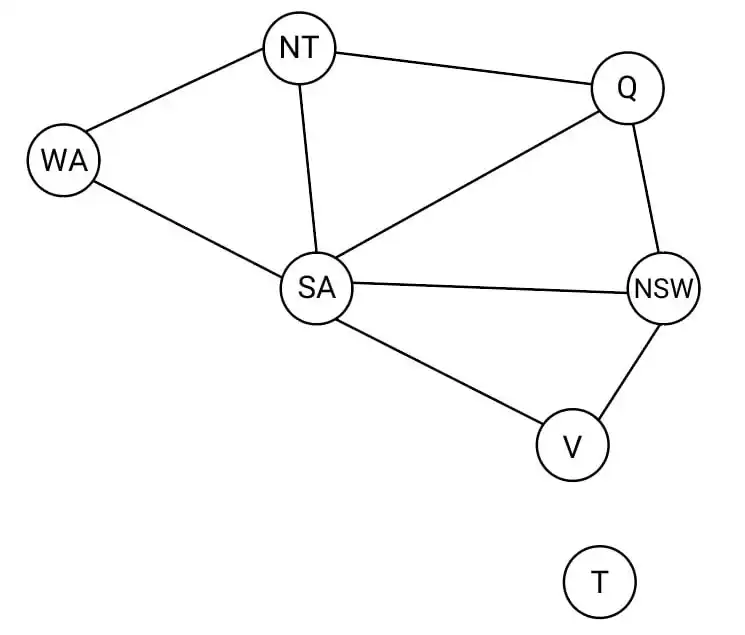
دشوار می‌خواهیم گراف زیر را با سه رنگ رنگ‌آمیزی نماییم. هیچ دو رنگ مشابهی نمی‌توانند کنار یکدیگر باشند. اگر مقدار NT = red و V = red باشد، آنگاه این ناسازگاری با کدامیک از روش‌های زیر قابل تشخیص است؟ مسائل ارضای محدودیت
گزینه 3 صحیح است.
یادآوری :
Forward checking : در این روش با هر مقداردهی با متغیرها دامنه مقادیر همه متغیرهای بدون مقدار که دارای محدودیت با متغیر مقداردهی شده می‌باشند بررسی و بروزرسانی می‌شوند. در این حالت در صورتی که به دامنه تهی برای یکی از متغیرها برسیم ناسازگاری رخ داده و عقبگرد می‌کنیم.
Path consistency : سازگاری مسیر به این معنی است که اگر برای دو متغیر مقدار مجاز و معتبر وجود داشته باشد برای متغیر سوم نیز حداقل یک مقدار مجاز و معتبر وجود دارد پس اگر در گراف به ازای هر سه متغیر نکته بالا برقرار باشد می‌توان گفت سازگاری مسیر داریم.
Arc Consistency : همان سازگاری کمان است که در این روش با هر مقداردهی به متغیرها دامنه مقادیر همه متغیرهای بدون مقدار که دارای محدودیت با متغیر مقداردهی شده می باشند بررسی و بروزرسانی می‌شوند. در این حالت در صورتی که به دامنه تهی برای یکی از متغیرها برسیم ناسازگاری رخ میدهد.
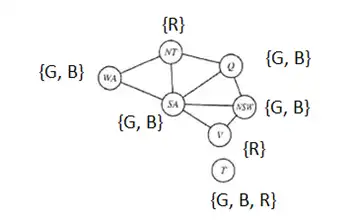
در این سوال با اعمال Forward checking می‌توان به شکل بالا رسید که همانطور که مشاهده میشود دامنه‌ی هیچ متغیر تهی نشده است .
از طرفی سازگاری کمان نیز برقرار است چرا که به ازای هر یال می‌توان مقادیری را به دو سر آن با فرض اینکه محدودیت‌ها مطابق شکل بالا هستند اختصاص داد.
اما ناسازگاری مسیر در گراف داده شده برقرار نیست چرا که به ازای سه متغیر {SA, Q, NSW} برای هر دو متغیر امکان مقداردهی معتبر وجود دارد اما امکان مقداردهی برای متغیر سوم نیست و این امر باعث ناسازگاری مسیر میشود.
توجه: در سؤال اصلی کنکور، صورت سوال NT = red و V = green است که نادرست است و هیچکدام از روش‌های ذکر شده در گزینه‌ها امکان تشخیص این ناسازگاری را ندارند زیرا با این رنگ‌ها می‌توان یک ترکیب درست برای تمام متغیرها یافت، (این تست کنکور از دفترچه حذف شده است.) در اینجا (برای تمرین) فرضیات سوال را به NT = red و V = red تغییر داده‌ایم تا بتوان به حل سوال پرداخت.
دشوار یک مسئله ارضای محدودیت با چهار متغیر C، B، A و D را درنظر بگیرید که در آن دامنه تمام متغیرها مجموعه $\left\{\mathrm{1,\ 2,\ 3,\ 4}\right\}$ است. این مسئله دارای محدودیت‌های $\mathrm{A\ <\ B\ <\ C\ <\ D\ }$ و C=A + 3 است. می‌دانیم برای عدد طبیعی k، با حذف برخی مقادیر از دامنه متغیرها، ممکن است بتوان یک مسئله ارضای محدودیت را به یک مسئله strongly k-consistent تبدیل کرد. حال با فرض حذف مقادیر لازم از دامنه متغیرها، کدام مورد در خصوص مسئله فوق درست است؟ مسائل ارضای محدودیت
گزینه 3 صحیح است.
نکات :
یک مسئله ارضا محدودیت زمانی قویا K سازگار است که به ازا تمای iهای کوچکتر مساوی K این مسئله i-سازگار باشد.
یک مسئله ارضا محدودیت زمانی k-سازگار است که اگر به ازای هر k-1 متغیر از مسئله مقدار سازگار وجود داشته باشد آنگاه حداقل یک مقدار مجاز برای k امین متغیر مسئله نیز وجود داشته باشد.
با توجه به این تعریف این مسئله ۱-سازگار است به این معنی که اگر فقط یک متغیر را در نظر بگیریم امکان مقداردهی به آن وجود دارد و محدودیت‌های یکانی نداریم.
اما این مسئله ۲-سازگار نیست چرا که نمی‌توان مقداردهی برای متغیرها داشت که محدودیت‌های دوتایی را نقض نکند. محدودیت دوتایی C= A + 3 با توجه به مقادیر دامنه متغیرها باعث میشود که A = 1 و C = 4 در نظر گرفته شود از طرفی عبارت $A \lt B \lt C \lt D$ یک عبارت ترکیبی از محدودیت‌های دوتایی است و محدودیت $C \lt D$ از محدودیت بدست می‌آید، حال با توجه به مقداری که A و C با توجه به محدودیت C= A + 3 گرفتند و محدودیت $C \lt D$، این محدودیت قابل برطرف کردن نیست و دامنه C خالی میشود و بنابراین و امکان مقداردهی به متغیرها با در نظر گرفتن همه محدودیت‌ها وجود ندارد و بنابراین دو سازگاری نداریم و گزینه 3 صحیح است.
دشوار برای کاهش زمان حل مسئله ارضای محدودیت که فضای گرافی دارد. یکی از روش‌ها تبدیل گراف به درخت است و این موضوع با تعریف مجموعه راس‌هایی از گراف که با حذف آنها گراف به درخت تبدیل میشود، قابل انجام است. به این مجموع cut – set گفته میشود کدام یک از گزینه‌های زیر بیانگر زمان مسئله CSP به روش cut – set conditinning است. اگر مجموعه cut – set دارای m عضو باشد؟ (n تعداد متغیر و d تعداد اعضای دامنه هر متغیر است) مسائل ارضای محدودیت
دو راه حل برای تبدیل گراف به درخت وجود دارد که عبارتند از Removing node و collapsing nodes. در روش حذف گره مجموعه cut – set تشکیل میشود و در هر مرحله هر عضو از این مجموعه m عضوی یکی از مقادیر d تایی خود را دریافت میکند و آن مقدار از همسایگان حذف میشود و درخت (n – m) گره‌ای با مرتبه $d^\mathrm{2}$ حل میشود و در نهایت پاسخ درخت و مجموعه cut – set اجتماع شده تا جواب نهایی حاصل میشود. بنابراین مرتبه زمانی برابر $d^m\ast(n-m)d^\mathrm{2}$ است.
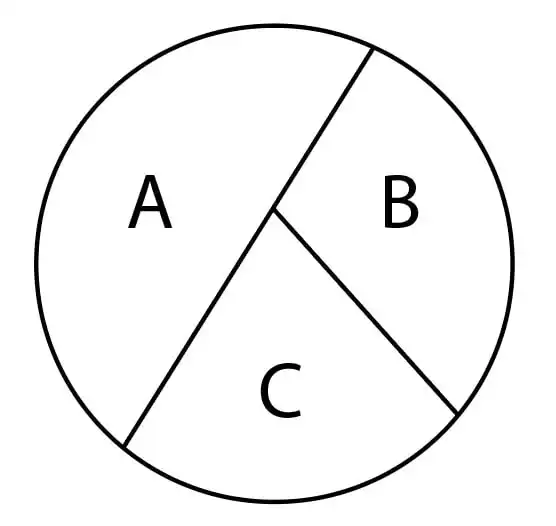
دشوار مسأله ارضای محدودیت (Constraint Satisfaction) رنگ کردن نقشه زیر را درنظر بگیرید. فرض کنید می‌خواهیم این نقشه را با تنها یک رنگ، رنگ‌آمیزی کنیم (شهرهای مجاور نباید هم‌رنگ باشند). با این فرض، گراف محدودیت (Constraint Graph) این مسأله به ازای چه مقدار (مقادیر) K، دارای خاصیت K-Consistency است؟ مسائل ارضای محدودیت
گزینه 4 صحیح است.
ابتدا به تعریف سازگاریk- می‌پردازیم. این سازگاری در واقع مشابه بسط سازگاری مسیر (path consistency) می‌باشد که برای تعداد متغیر بیشتری تعریف میشود. در یک مسئله ارضا محدودیت گفته میشود که سازگاری-k برقرار است اگر به ازای هر k-1 متغیر از cps مقدار سازگار وجود داشته باشد آنگاه حداقل یک مقدار مجاز و معتبر برای k امین متغیر cps نیز وجود داشته باشد.
1- consistent : همان سازگاری نود است که محدودیت‌هایی یکانی را بررسی میکند به این معنی است که آیا بدون توجه به سایر نودها مقداری وجود دارد که به هر نود نسبت دهیم.
2- consistent : همان سازگاری کمان است که در این روش با هر مقداردهی به متغیرها دامنه مقادیر همه متغیرهای بدون مقدار که دارای محدودیت با متغیر مقداردهی شده می باشند بررسی و بروزرسانی می‌شوند. در این حالت در صورتی که به دامنه تهی برای یکی از متغیرها برسیم ناسازگاری رخ میدهد.
3- consistent : همان سازگاری مسیر است که بیان میکند اگر برای دو متغیر مقدار مجاز و معتبر وجود داشته باشد برای متغیر سوم نیز حداقل یک مقدار مجاز و معتبر وجود دارد پس اگر در گراف به ازای هر سه متغیر نکته بالا برقرار باشد می‌توان گفت سازگاری مسیر داریم.
حال به حل مسئله می‌پردازیم. در این مسئله گراف محدودیت مطابق شکل زیر بدست می‌آید.
برای اینکه مسئله ۱-سازگار باشد نیاز است که بدون توجه به سایر نودها مقداری وجود داشته باشد که به هر نود نسبت دهیم و با توجه به اینکه در این حالت هر کدام از متغیرها یک رنگ را در دامنه خود دارند این سازگاری برقرار است.
برای بررسی ۲-سازگار بودن مسئله ابتدا به گره A تنها رنگ مسئله را نسبت می‌دهیم در این صورت با توجه به اینکه گره A با گره‌های B و C مجاور است این رنگ از دامنه این متغیر حذف میشود و دامنه این متغیرها تهی می‌شوند پس این سازگاری نقض میشود و این مسئله ۲-سازگار نیست.
در نهایت نیز برای بررسی ۳-سازگار بودن از تعریف گفته شده استفاده می‌کنیم. اگر برای دو متغیر مقدار مجاز و معتبر وجود داشته باشد آنگاه برای متغیر سوم نیز حداقل یک مقدار مجاز و معتبر وجود دارد. در این مسئله شرط اولیه مسئله برقرار نیست یعنی برای هر دو متغیری که در نظر بگیریم، مقداردهی مجاز و معتبر وجود ندارد پس در این حالت سمت چپ استنتاج flase میشود در نتیجه می‌توان گفت استنتاج برقرار و درست است و این مسئله ۳-سازگار است. در نتیجه گزینه ۴ درست می‌باشد.
(نکته : در منطق گزاره‌ای داشتیم $p \rightarrow q$ برقرار است اگر p نادرست باشد یا p درست و q هم درست باشد. در این مسئله حالت اول برقرار شده است)
متوسط در حل یک مسئله ارضای قیود با استفاده از روش جستجوی Backtracking، که در آن AC3 در هر گره اجرا میشود، کدامیک از موارد زیر درست است؟ مسائل ارضای محدودیت
گزینه 2 صحیح است. الگوریتم backtracking به همراه AC3 در حل مسائل CSP استفاده میشود.
نحوه عملکرد الگوریتم:
نحوه عملکرد این الگوریتم به این گونه است که در هر مرحله مقداری از دامنه یک متغیر را به آن نسبت میدهد و سپس الگوریتم AC3 را اجرا میکند، اگر دامنه هیچ متغیری تهی نشد به سراغ متغیر دیگر می‌رود و از میان دامنه مقادیر باقی مانده به آن متغیر نسبت میدهد، این عمل تا جایی ادامه پیدا میکند که تمام متغیرها مقداردهی شوند و مسئله حل شود. حال اگر با اجرای AC3 در یکی از مراحل دامنه یکی از متغیرها تهی شود، به سراغ متغیری که در این مرحله به آن مقدار دادیم می‌رویم و مقدار دیگری از دامنه آن را به آن نسبت می‌دهیم، مقداری در دامنه باقی نمانده بود به سراغ متغیری که قبل از این متغیر به آن مقدار نسبت داده بودیم می‌رویم و مقدار آن را تغییر می‌دهیم ولی باز اگر مشکل بود به عقب‌تر می‌رویم، این روند تاجایی ادامه می‌یابد تا به متغیر اولیه که به آن مقدار نسبت دادیم برسیم، اگر این متغیر نیز تمام دامنه‌اش چک شده بود و جوابی بدست نیامده بود به این نتیجه می‌رسیم که این مسئله جواب ندارد.
بررسی گزینه‌ها:
گزینه ۱:
اگر در مرحله‌ای دامنه متغیری تهی شود الگوریتم backtracking به سراغ نسبت دادن مقدار دیگری به متغیر فعلی می‌رود و یا به سراغ متغیرهای مقداردهی شده قبلی می‌رود تا مقدار آنها را عوض کند. این به این معنی است که ممکن است همچنان جواب برای مسئله وجود داشته باشد. بنابراین این گزینه نادرست است.
مثال: در این مثال باید رنگ‌ها را برای ۳ ناحیه جوری مشخص کنیم که رنگ هر ناحیه متفاوت باشد. دامنه رنگ‌های هر ناحیه داخل آن نوشته شده است.
اگر الگوریتم داده شده را از ناحیه سمت چپ شروع کنیم و این الگوریتم ابتدا رنگ آبی و یا سبز را برای این ناحیه در نظر بگیرد، مشخص است که با اجرای الگوریتم AC3 حتما دامنه یکی از ناحیه‌ها تهی میشود، ولی از روی دامنه ناحیه‌ها معلوم است که این مسئله جواب دارد.
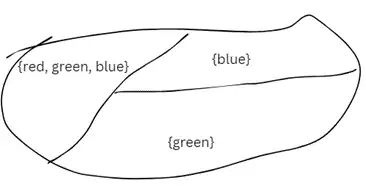
به یاد داشته باشید که تنها زمانی الگوریتم اعلام میکند که مسئله جواب ندارد که در متغیر اولی که به سراغش می‌رود باشد و تمام دامنه مقادیر آن را تست کرده باشد.
گزینه ۲:
این گزینه درست است، زیرا هر ارتباط میان دو گره یکبار در ابتدای اجرای AC3 چک میشود و یکبار هم به ازای هرباری که یک مقدار از دامنه متغیر حذف میشود البته این در صورتی است که حذف آن مقدار دامنه متغیر را تهی نکند، بنابراین اگر یک متغیر d عضو در دامنه ابتدایی خود داشته باشد با حذف همه آنها d-1 بار پردازش صورت می‌گیرد که بهمراه بار اول پردازش در مجموع d پردازش صورت می‌گیرد.
گزینه ۳:
اگر اتفاق گفته شده رخ دهد هنوز مشخص نیست که مسئله جواب داشته باشد زیرا AC3 تنها محدودیت دو به دو میان اعضا را چک میکند و ممکن است که مسئله محدودیت‌هایی با مشارکت اعضای بیشتر داشته باشد که الگوریتم AC3 آنها را نبیند.
برای همین هم در الگوریتم گفته شده اگر این اتفاق رخ دهد به سراغ متغیر دیگری که مقداردهی نشده می‌رود و به آن یک مقدار از دامنه فعلی‌اش را میدهد و دوباره AC3 را اجرا میکند و...
بنابراین این گزینه نادرست است.
به مثال ساده زیر توجه کنید:
مثال: ۳ متغیر داریم که هر کدام دامنه‌ای از اعداد دارد، هدف انتخاب یک عدد برای هر متغیر است به گونه‌ای که جمع اعداد انتخابی کمتر از ۱۰ شود.
۳ متغیر و دامنه‌هایشان:
$A=\left\{6,\ 7\right\},\ B=\left\{2\right\},\ C=\left\{3\right\}$
حال اگر الگوریتم داده شده از متغیر A شروع کرده و ابتدا عدد ۶ را انتخاب کند با اجرای الگوریتم AC3 دامنه‌ها به صورت زیر می‌شوند: (زیرا AC3 تنها محدودیت را هر بار بین دو متغیر چک میکند و همانطور که می‌بینید شرط با چک کردن دو به دو برقرار است.)
$A=\left\{6\right\},\ B=\left\{2\right\},\ C=\{3\}$
در این مرحله پس از AC3 دامنه متغیرها همگی غیر تهی شدند ولی مشخص است که مسئله در کل جواب ندارد.
گزینه ۴:
یک مقدار مجاز می‌تواند بسته به مقادیری که الگوریتم در هر مرحله به برخی از متغیرها نسبت میدهد حذف شود و یا باقی بماند، بنابراین اگر مقداری در مرحله‌ای حذف شد ممکن است با انجام عمل بازگشت (backtracking) و تغییر متغیرهای نسبت‌داده شده دوباره به مسئله بازگردد و حتی در جواب نهایی باشد.
بنابراین این گزینه نادرست است.
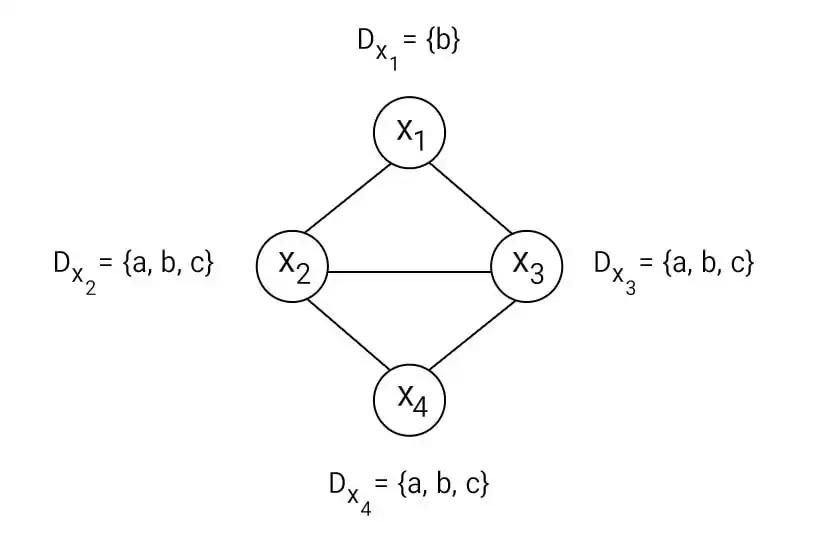
دشوار در مسئله CSP با چهار متغیر $\mathrm{X}_\mathrm{4}$، $\mathrm{X}_\mathrm{3}$، $\mathrm{X}_\mathrm{2}$، $\mathrm{X}_\mathrm{1}$ و گراف محدودیت (که هر لینک آن محدودیت یکسان نبودن مقدار متغیرهای دو سر آن لینک را نشان میدهد) مشخص شده است. دامنه‌ی متغیرها هم کنار آنها نشان داده شده است. بعد از اعمال AC3 دامنه‌ی متغیرها به چه صورت درمی‌آید؟ مسائل ارضای محدودیت
گزینه 3 صحیح است.
الگوریتم AC-3 معروف‌ترین الگوریتم سازگاری کمان است که می‌تواند در زمان پیش پردازش یا اجرا اعمال شود. روش کار این الگوریتم در حالت پیش پردازش به این صورت است که در مرحله اول همه کمان‌های مسئله در یک صف قرار می‌گیرند و سپس تا زمانی که صف خالی نشده است موارد زیر را اجرا می‌کنیم :
یک یال از صف برداشته ($x \rightarrow y$) و مقادیر دامنه x که باعث ناسازگاری کمان می‌شوند از دامنه x حذف شده و همه کمان‌هایی که به x وارد می‌شوند مجددا به صف اضافه می‌شوند.
در این الگوریتم در حالت پیش پردازش در صورتی که دامنه تهی برای یکی از گره‌ها مشاهده شود با ناسازگاری مواجه می‌شویم و الگورتیم متوقف میشود اما در حالتی که در حین اجرا این الگوریتم روی مسئله cps اعمال میشود اگر دامنه تهی مشاهده شود باید عقبگرد انجام شود تا حالت‌های دیگر مقداردهی به گره‌ها نیز بررسی شوند. در این صورت بسته به اینکه در چه مرحله‌ای باشیم قدم بعدی هنگام مواجه به دامنه‌ی تهی می‌تواند عقبگرد یا توقف باشد.
در مسئله داده شده ، این الگوریتم را در حالت پیش پردازش اجرا می‌کنیم. ابتدا کمان $x_2 \rightarrow x_1$ را در نظر می‌گیریم. در این حالت فقط مقدار b از دامنه $x_2$ است که باعث ناسازگاری میشود پس این مقدار را از دامنه $x_2$ حذف می‌کنیم. پس از آن کمان $x_3 \rightarrow x_1$ را بررسی می‌کنیم. در این حالت نیز مشابه حالت قبلی فقط مقدار b از دامنه $x_3$ حذف میشود. در مرحله بعد با بررسی کمان $x_3 \rightarrow x_2$ هیچ مقدار حذف نمی‌شود چرا که به ازای هر مقداردهی به یک سر این یال مقدار معتبری برای سر دیگر این یال وجود دارد. یال‌های $x_3 \rightarrow x_4$ و $x_2 \rightarrow x_4$ نیز به همین دلیل باعث حذف هیچ مقداری از دامنه متغیرها نمی‌شوند. مقدارهای باقی‌مانده برای هر کدام از متغیرها با توجه به توضیحات بالا معادل گزینه سوم می‌باشد.
نمونه سوالات فصل منطق گزاره ای درس هوش مصنوعی
دشوار می‌خواهیم ارضاپذیری جمله زیر را با کمک الگوریتم DPLL بررسی کنیم: منطق گزاره‌ای
$(A\vee C\vee\lnot E)\land(B\vee C\vee D)\land(A\vee\lnot B\vee E)$
فرض کنید تاکنون سمبل‌های A و B به ترتیب مقادير True و False گرفته باشند. در مرحله بعدی از الگوریتم:
هیورستیک "نماد محض"، سمبلی که در تمام عبارات فصلی در یک جمله CNF با علامت یکسانی ظاهر شده باشد را مقداردهی میکند (سمبل‌های محض بدون $\lnot$ را به True و سمبل‌های محض با $\lnot$ را به False مقداردهی میکند). در جمله داده شده، سمبل C یک نماد محض است چون در تمام عبارات فصلی به صورت بدون $\lnot$ ظاهر شده است. بنابراین سمبل به True مقداردهی میشود.
متوسط کدام عبارت در $g(y,f(b),z)$ ورد الگوریتم $DPLL$ برای عبارت‌های منطق گزاره‌ای نادرست است؟ منطق گزاره‌ای
الگوریتم DPLL می‌تواند سازگاری یک مجموعه عبارت را تشخیص دهد. اگر نقیض یک گزاره را به یک پایگاه دانش اضافه کنیم، در صورتی که الگوریتم بتواند سازگاری این مجموعه را تشخیص دهد، حکم قابل اثبات است و در غیر این صورت، قابل اثبات نیست. این الگوریتم فضای حالت را به صورت محلی جست‌وجو نمی‌کند.
آسان پایگاه دانش KB به شکل روبرو را در نظر بگیرید. کدام گزینه درست است؟ منطق گزاره‌ای
$\forall x\ \exists y\ P\left(x.y\right)\Rightarrow\ \left(\forall y\ Q\left(y.x\right)\Rightarrow\ R\left(y.x\right)\right)$
$\forall x\ \exists y\ R\left(x.y\right)\Rightarrow S\left(y\right)$
$Q(C.A)$
$Q(B.C)$
$P\left(A.B\right)$
از عبارت اول و فکت‌های $P(A,B)$ و $Q(C,A)$ می‌توان نتیجه گرفت $R(C,A)$ برقرار است و در نتیجه طبق عبارت دوم $S(A)$ استنتاج خواهد شد.
متوسط فرض کنید در یک پایگاه دانش داشته باشیم: منطق گزاره‌ای
$\mathrm{\neg }\mathrm{C\ }\mathrm{\Rightarrow }\mathrm{\ \neg K}$
$\mathrm{C\ }\mathrm{\Rightarrow }\mathrm{\ A\ }\mathrm{\vee }\mathrm{\ }\mathrm{B}$
$\mathrm{B\ }\mathrm{\Rightarrow }\mathrm{\ R\ }\mathrm{\vee }\mathrm{\ C}$
$\mathrm{K\ }\mathrm{\wedge }\mathrm{\ \neg M}$
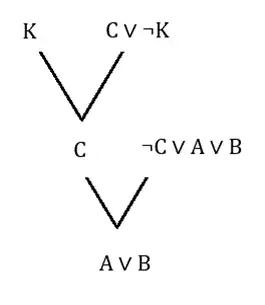
کدامیک از جملات زیر با استفاده از Resolution از این پایگاه قابل استنتاج نیست؟
گزینه 1 صحیح است.
ابتدا جملات را به فرم CNF تبدیل می‌کنیم.
$C \vee \neg K$
$\neg C \vee A \vee B$
$\neg B \vee R \vee C$
$K $
$\neg M$
$\neg C \vee A \vee B$
$\neg B \vee R \vee C$
$K $
$\neg M$
گزینه ۱: این گزینه از روی پایگاه دانش داده شده قابل استنتاج نیست.
گزینه ۲: درخت استنتاج عبارت متناظر با این گزینه در شکل زیر نشان داده شده است.
گزینه ۳ : از آنجایی که طبق پایگاه دانش K همواره درست است پس or آن با هر عبارت دیگری نیز همواره درست است.
گزینه ۴ : پایگاه دانش نتیجه میدهد True نیز عبارتی همواره درست است.
نمونه سوالات فصل منطق مرتبه اول درس هوش مصنوعی
متوسط یکسان سازی عبارت $g(C,x,f(f(x)))$. با کدام عبارت ممکن است؟ (C و D ثابت اسکولم است). منطق مرتبه اول
در $g(C, x, f(f(x)))$ عبارت $C$ نشان دهنده ثابت اسکولم است که سور وجودی را نشان میدهد.$f(f(x))$ به $x$ وابسته است. می‌توان به جای $y$ از $C$، به جای $x$ از $f(b)$ و به جای $z$ از $f(f(f(b)))$ استفاده کرد.
دشوار کدام یک از گزینه‌های زیر نتیجه منطقی جملات مقابل است؟ منطق مرتبه اول
$\mathrm{\exists }\mathrm{xCat}\left(\mathrm{x}\right)\mathrm{\wedge }\mathrm{Owns}\left(\mathrm{Hamid,\ x}\right)\mathrm{\ }$
$\mathrm{\forall }\mathrm{x}\left(\exists \mathrm{y}\left(\mathrm{Cat}\left(\mathrm{y}\right)\wedge \mathrm{Owns}\left(\mathrm{x\ ,\ y}\right)\right)\Rightarrow \mathrm{Animal}\mathrm{-}\mathrm{Lover}\left(\mathrm{x}\right)\right)\mathrm{\ }$
$\mathrm{\forall }\mathrm{x}\mathrm{\forall }\mathrm{y}\left(\mathrm{Animal}\mathrm{-}\mathrm{Lover}\left(\mathrm{x}\right)\wedge \mathrm{Animal}\left(\mathrm{y}\right)\Rightarrow \neg \mathrm{Kills}\left(\mathrm{x\ ,\ y}\right)\right)\mathrm{\ }$
$\mathrm{Kills}\left(\mathrm{Hamid,\ Pupu}\right)\mathrm{\ }\mathrm{\vee }\mathrm{\ Kills}\left(\mathrm{Behzad,\ Pupu}\right)\mathrm{\ }$
$\mathrm{Fish}\left(\mathrm{Pupu}\right)\mathrm{\ }$
$\mathrm{\forall }\mathrm{x}\left(\mathrm{Fish}\left(\mathrm{x}\right)\Rightarrow \mathrm{Animal}\left(\mathrm{x}\right)\right)\mathrm{\ }$
$\mathrm{\neg Kills}\left(\mathrm{Hamid,\ Behzad}\right)$
گزینه 3 صحیح است.
در ابتدا گزاره ها را به فارسی برمی‌گردانیم:
1 – گربه‌ای وجود دارد که حمید صاحب آن است.
2- هر کسی که صاحب گربه است،دوستدار حیوانات است.
3- هر کسی که دوستدار حیوانات است، هیچ حیوانی را نمی‌کشد.
4- حمید یا بهزاد پوپا را کشته‌اند.
5- پوپا ماهی است.
6- هر ماهی ، حیوان است.
7- حمید، بهزاد را نکشته است.
حال با توجه به جملات بالا گزینه ها را بررسی می‌کنیم. گزینه اول : حمید دوستدار حیوانات است چرا که صاحب گربه است و هر کسی که دوستدار حیوانات باشد، حیوان را نمی‌کشد پس حمید پوپا را نکشته است. طبق (4) نتیجه می‌گیریم که بهزاد پوپا را کشته است پس بهزاد قاتل پوپا است (نه ماهی !). گزینه دوم : حمید دوستدار حیوانات است نه گربه. گزینه سه : همان طور که اشاره کردیم بهزاد قاتل پوپا است پس این گزاره به دلیل اینکه دارای ترکیب فصلی است و قسمت اول آن همواره درست است گزاره درست و جواب سوال است. گزینه چهارم : هر دو بخش این گزینه نادرست است چرا که قاتل پوپا بهزاد است نه حمید یا گربه.
دشوار با این فرض که متغیر $x$ در $Q$ به‌صورت آزاد (free) ظاهر نشده است، مقدار کدامیک از عبارات زیر در منطق مسندات (predicate logic) نادرست (False) است؟ منطق مرتبه اول
گزینه 2 صحیح است.
در این مسئله شروع به ساده‌سازی گزینه‌ها با استفاده از قانون زیر می‌کنیم تا ببینم که کدامیک نادرست است. (در این سوال به محل قرارگیری سور عمومی و وجودی دقت کنید)
$ \mathop{P}^{}\to Q\ \ \equiv \ \neg P\ \vee \ Q $
$ \mathrm{\exists }x\left(P\left(x\right)\to Q\right)\ \ \equiv \ \mathrm{\exists }x\left(\neg P\left(x\right)\ \vee \ Q\right) $
$ \mathrm{\exists }x\ \ P\left(x\right)\to Q\equiv \ \mathrm{\forall }x\ \neg P\left(x\right)\ \vee \ Q $
$ \mathrm{\exists }x\ \ P\left(x\right)\to Q\equiv \ \mathrm{\forall }x\ \neg P\left(x\right)\ \vee \ Q $
گزینه ۱ : در این گزینه ابتدا رابطه یک طرفه در سمت راست وچپ را ساده‌سازی می‌کنیم.
$ \left(\mathrm{\exists }x\left(P\left(x\right)\to Q\right)\right)\to \left(\mathrm{\forall }xP\left(x\right)\to Q\right) $
$ \left(\mathrm{\exists }x\left(\neg P\left(x\right)\ \vee \ Q\right)\right)\to \left(\mathrm{\exists }x\ \neg P\left(x\right)\ \vee \ Q\right) $
$ \left(\mathrm{\exists }x\left(\neg P\left(x\right)\ \vee \ Q\right)\right)\to \left(\mathrm{\exists }x\ \neg P\left(x\right)\ \vee \ Q\right) $
از آنجایی که متغیر x در Q ظاهر نشده است می‌توان نتیجه گرفت که دو طرف عبارت بالا با یکدیگر معادلند.
گزینه ۲ : در این گزینه ابتدا رابطه یک طرفه در سمت راست وچپ را ساده‌سازی می‌کنیم.
$ (\forall xP(x)\rightarrow Q)\rightarrow(\forall x(P(x)\rightarrow Q)) $
$ (\exists x\ \lnot P(x)\ \vee\ Q)\rightarrow(\forall x(\lnot P(x)\ \vee\ Q)) $
$ (\exists x\ \lnot P(x)\ \vee\ Q)\rightarrow(\forall x(\lnot P(x)\ \vee\ Q)) $
بعد از ساده‌سازی می‌بینیم که در عبارت دوم، طرفین رابطه معادل یکدیگر نشدند و از سور وجودی نیز نمی‌توان سور عمومی را نتیجه گرفت.
گزینه ۳ : در این گزینه ابتدا رابطه یک طرفه در سمت راست وچپ را ساده‌سازی می‌کنیم.
$ (\exists x\ P(x)\rightarrow Q)\rightarrow(\forall x(P(x)\rightarrow Q)) $
$ (\forall x\ \lnot P(x)\ \vee\ Q)\rightarrow(\forall x\ (\lnot P(x)\ \vee\ Q)) $
از آنجایی که متغیر x در Q ظاهر نشده است می‌توان نتیجه گرفت که دو طرف عبارت بالا با یکدیگر معادلند.
گزینه ۴ : در این گزینه ابتدا رابطه یک طرفه در سمت راست وچپ را ساده‌سازی می‌کنیم.
$ (\exists xP(x)\rightarrow Q)\rightarrow(\exists x(P(x)\rightarrow Q)) $
$ (\forall x\ \lnot P(x)\ \vee\ Q)\rightarrow(\exists x(\lnot P(x)\ \vee\ Q)) $
در این گزینه همان طور که در عبارت دوم می‌بینم طرفین تساوی معادل یکدیگر نشدند اما در یک طرف سور عمومی داریم و در یک طرف سور وجودی و فلش رابطه به سمت سور وجودی است و از آنجایی که از سور عمومی می‌توانیم سور وجودی را نتیجه بگیریم این عبارت، عبارتی درست است.
دشوار کدام گزینه مشخص‌کننده کلوز‌هایی است که از جمله منطق مرتبه اول زیر به‌دست می‌آیند؟ منطق مرتبه اول
$\forall \mathrm{x\ }\mathrm{\exists }\mathrm{y\ A}\left(\mathrm{x}\right)\mathrm{\wedge }\mathrm{A}\left(\mathrm{y}\right)\mathrm{\Rightarrow }\mathrm{\exists }\mathrm{zB}\left(\mathrm{x\ ,\ z}\right)\mathrm{\wedge }\mathrm{A}\left(\mathrm{z}\right)\mathrm{\ }$
گزینه صحیح 2 است.
نکته یادآوری :
در این مسئله شروع به ساده‌سازی گزینه‌ها با استفاده از قانون زیر می‌کنیم. (در این سوال به محل قرارگیری سور عمومی وجودی دقت کنید)
$\mathop{P}^{}\to Q\ \ \equiv \ \neg P\ \vee \ Q$
$\mathrm{\exists }x\left(P\left(x\right)\to Q\right)\ \ \equiv \ \mathrm{\exists }x\left(\neg P\left(x\right)\ \vee Q\right)$
$\mathrm{\exists }x\ \ P\left(x\right)\to Q\equiv \ \mathrm{\forall }x\ \neg P\left(x\right)\ \vee Q$
$\mathrm{\exists }x\ \ P\left(x\right)\to Q\equiv \ \mathrm{\forall }x\ \neg P\left(x\right)\ \vee Q$
عبارت داده شده در صورت سوال را مرحله به مرحله به فرم نرمال عطفی تبدیل می‌کنیم. ابتدا را با استفاده از نکات بالا ساده می‌کنیم.
$\mathrm{\forall }\mathrm{x}~\mathrm{\exists }\mathrm{y}~\mathrm{A}\mathrm{(}\mathrm{x}\mathrm{)}\mathrm{\wedge }\mathrm{A}\mathrm{(}\mathrm{y}\mathrm{)}\mathrm{\Rightarrow }\mathrm{\exists }\mathrm{zB}\mathrm{(}\mathrm{x}~,~\mathrm{z}\mathrm{)}\mathrm{\wedge }\mathrm{A}\mathrm{(}\mathrm{z}\mathrm{)}~$
$\mathrm{\forall }\mathrm{x}~\neg \left(\mathrm{\exists }\mathrm{y}~\mathrm{A}\left(\mathrm{x}\right)\mathrm{\wedge }\mathrm{A}\left(\mathrm{y}\right)\right)\mathrm{\vee }\mathrm{\exists }\mathrm{zB}\left(\mathrm{x}~,~\mathrm{z}\right)\mathrm{\wedge }\mathrm{A}\left(\mathrm{z}\right)$
$~\mathrm{\forall }x\mathrm{\ }(~\mathrm{\forall }\mathrm{y}~\neg \mathrm{A}\mathrm{(}\mathrm{x}\mathrm{)}\mathrm{\vee }\neg \mathrm{A}\mathrm{(}\mathrm{y}\mathrm{))}\mathrm{\vee }\mathrm{\exists }zB\left(x~,~z\right)\mathrm{\wedge }A\left(z\right)$
در مرحله بعد سور وجودی z باتوجه به اینکه به صورت عمومی وابسته است با تابع اسکالم جایگذاری میشود.
$~\mathrm{\forall }x\mathrm{\ }(~\mathrm{\forall }\mathrm{y}~\neg \mathrm{A}\mathrm{(}\mathrm{x}\mathrm{)}\mathrm{\vee }\neg \mathrm{A}\mathrm{(}\mathrm{y}\mathrm{))}\mathrm{\vee }B\left(x~,~f(x)\right)\mathrm{\wedge }A\left(~f(x)\right)$
در مرحله بعد نیز سورهای عمومی را حذف می‌کنیم و از قانون پخشی برای ساده سازی استفاده می‌کنیم.
$(\neg \mathrm{A}\mathrm{(}\mathrm{x}\mathrm{)}\mathrm{\vee }\neg \mathrm{A}\mathrm{(}\mathrm{y}\mathrm{)})\mathrm{\ }\mathrm{\vee }B\left(x~,~f(x)\right)\mathrm{\wedge }A\left(~f(x)\right)$
$(\neg \mathrm{A}\mathrm{(}\mathrm{x}\mathrm{)}\mathrm{\vee }\neg \mathrm{A}\mathrm{(}\mathrm{y}\mathrm{)}\mathrm{\vee }B\left(x~,~f(x)\right))\ \ \mathrm{\wedge }\mathrm{\ }(\neg \mathrm{A}\mathrm{(}\mathrm{x}\mathrm{)}\mathrm{\vee }\neg \mathrm{A}\mathrm{(}\mathrm{y}\mathrm{)\ }\mathrm{\vee }A\left(~f(x)\right))$
و می‌توان دید که and عبارات داده شده در گزینه ۲ مطابق با عبارت بدست آمده در بالا است.
دشوار کدامیک از عبارات زیر درست است؟ منطق مرتبه اول
گزینه 1 و 4 صحیح است.
گزینه ۱ : این گزینه درست است و زنجیره جلورو برای استنتاج در منطق مرتبه اول روی کلازهای معین کامل است.
گزینه ۲ : زنجیره جلورو در منطق گزاره‌ای روی کلازهای به فرم نرمال هورن کامل کاذب است.
گزینه ۳ : برای استنتاج در منطق گزاره‌ای، روش رزولوشن (Resolution) روی عبارات به فرم CNF کامل (complete) است.
گزینه ۴ : برای استنتاج در منطق مرتبه اول الگوریتمی وجود ندارد که برای هر جمله غیر قابل استنتاج از پایگاه دانش اعلام کند که این جمله غیر قابل استنتاج است و ممکن است حتی در چنین شرایطی در حلقه بینهایت بیفتد پس با توجه به این نکته می‌توان گفت که استنتاج در منطق مرتبه اول یک مسئله نیمه تصمیم پذیر است و این گزینه نیز درست است.
نمونه سوالات فصل عدم قطعیت درس هوش مصنوعی
دشوار فرض کنید چهار متغیر تصادفی دودویی D ,C ,B ,A داریم که با شبکه بیزی زیر مدل شده‌اند. مقدار $P(A=1|B=0\ , \ D=1)$ چقدر است؟ عدم قطعیت
| $\mathbf{A\ \ \ \rightarrow \ \ \ \ B}$ | ||
| $\downarrow \ \ \ \ \ \ \ \ \ \ \ \ \ \ \downarrow$ | ||
| $C\ \ \ \ \rightarrow \ \ \ D$ | ||
| $\mathbf{P(D =}\text{0}\text{ | B=}\text{1}\text{ ,C=}\text{0}\text{)=}\text{0/5}$ | $P(B = \text{0}\text{ |A=}\text{0}\text{)=}\text{0/8}$ | $P(A = \text{0}\text{)=}\text{0/5}$ |
| $\mathbf{P(D =}\text{0}\text{ | B=}\text{0}\text{ , C=}\text{1}\text{)=}\text{0/5}$ | $P(B = \text{0}\text{ | A=}\text{1}\text{)=}\text{0/2}$ | $P(C = \text{0}\text{ | A=}\text{0}\text{)=}\text{0/1}$ |
| $\mathbf{P(D =}\text{0}\text{ | B=}\text{1}\text{ , C=}\text{1}\text{)=}\text{0}$ | $P(D = \text{0}\text{ | B=}\text{0}\text{ , C=}\text{0}\text{)=}\text{1}$ | $P(C = \text{0}\text{ | A=}\text{1}\text{)=}\text{0/8}$ |
گزینه 3 صحیح است. توزیع احتمال توأم متغیرها براساس مدل شبکه بیزی داده شده در صورت سوال را می‌توان به صورت زیر نوشت :
$P(A, B,C,D)=P(A)P(B|A)P(C|A)P(D|C,B)$
از طرفی صورت سوال مقدار $P(A=1| B=0, D=1)$ را خواسته است که برای محاسبه آن داریم :
$P(A=1|B=0,D=1)=\frac{P(A=1,B=0,D=1)}{P(B=0,D=1)}$
$=\ \frac{\mathrm{P}\left(\mathrm{A=1},\mathrm{\ B=0,\ D=1,\ }C=1\right)+\ \mathrm{P}\left(\mathrm{A=1},\mathrm{\ B=0,\ D=1,\ C=0}\right)}{\mathrm{P}\left(\mathrm{A=1,C=1},\mathrm{\ B=0,\ D=1}\right)+\ \mathrm{P}\left(\mathrm{A=1},C=0,\mathrm{\ B=0,\ D=1}\right)\mathrm{+\ P}\left(\mathrm{A=0},C=0,\ \mathrm{\ B=0,\ D=1}\right)+\ \mathrm{P}\left(\mathrm{A=0},\ C=1,\mathrm{\ B=0,\ D=1}\right)}$
برای محاسبه عبارت صورت کسر بالا داریم :
$\mathrm{P}\left(\mathrm{A=1},\mathrm{\ B=0,\ D=1,\ }C=1\right)+\ \mathrm{P}\left(\mathrm{A=1},\mathrm{\ B=0,\ D=1,\ C=0}\right)=\ $
$P(A=1)P(B=0|B=0A=1A=1)P(C=1|C=1A=1A=1)P(D=1|D=1C=1, B=0C=1, B=0)$
$+ P(A=1)P(B=0|B=0A=1A=1)P(C=0|C=0A=1A=1)P(D=1|D=1C=0, B=0C=0, B=0)= $
$P(A=1)P(B=0|B=0A=1A=1) ( P(C=1|C=1A=1A=1)P(D=1|D=1C=1, B=0C=1, B=0)+$
$P(C=0|C=0A=1A=1)P(D=1|D=1C=0, B=0C=0, B=0))$
$=0.5\ \times 0.2\ \ \left(\ 0.2\times 0.5\ +\ \ 0.8\times 0\right)=0.01$
و همچنین مخرج کسر نیز به‌صورت زیر محاسبه میشود :
$\mathrm{P}\left(\mathrm{A=1,C=1},\mathrm{\ B=0,\ D=1}\right)+\mathrm{P}\left(\mathrm{A=1},C=0,\mathrm{\ B=0,\ D=1}\right)\mathrm{+P}\left(\mathrm{A=0},C=0,\ \mathrm{B=0,\ D=1}\right)+\mathrm{P}\left(\mathrm{A=0},\ C=1,\mathrm{\ B=0,\ D=1}\right) = $
$0.01+ P(A=0)P(B=0|B=0A=0A=0)P(C=0|C=0A=0A=0)P(D=1|C=0,B=0)$
$+ P(A=0)P(B=0|B=0A=0A=0)P(C=1|C=1A=0A=0)P(D=1|D=1C=1, B=0C=1, B=0)=$
$=0.01+ P(A=0)P(B=0|B=0A=0A=0) (P(C=0|C=0A=0A=0)P(D=1|D=1C=0, B=0C=0, B=0)$
$+P(C=1|C=1A=0A=0)P(D=1|D=1C=1, B=0C=1, B=0))$
$=0.01+0.5\ \times 0.8\ \left(\ 0.1\times 0\ +\ 0.9\times 0.5\right)=0.19$
و در کل داریم :
$\mathrm{P(A=1|\ B=0,\ D=1)\ }\mathrm{=\ }\frac{\mathrm{P}\left(\mathrm{A=1},\mathrm{\ B=0,\ D=1}\right)\mathrm{\ }}{\mathrm{P}\left(\mathrm{\ B=0,\ D=1}\right)\mathrm{\ }}=\frac{0.01}{0.19}=\ \frac{1}{19}$
همانطور که در بالا می‌بینیم کمی حل سوال طولانی شد اما بسیاری از خطوط محاسبات در بالا را می‌توان بصورت ذهنی ساده‌سازی کرد و نیازی به نوشتن دقیق تمام مراحل نیست و من در اینجا برای اینکه مراحل مشخص باشد و هیج ابهامی وجود نداشته باشد تمام بخش‌ها را بصورت کامل نوشتم و در سر جلسه کنکور برای رسیدن به جواب باید تا حد امکان بصورت ذهنی ساده‌سازی کرد و بصورت خلاصه مراحل را نوشت.
آسان برای شبکه بیزین (Bayesian network) روبه‌رو، احتمال P(A, B, C, D, E) برابر کدام است؟ عدم قطعیت
گزینه 3 صحیح است.
برای بدست آوردن توزیع توأم از روی شبکه بیزین باید از احتمال هر متغیر به شرط پدرانش استفاده کنیم. متغیرهای A و B به هیچ متغیر دیگری وابسته نیستند (پدر ندارند) پس هر کدام از آنها را به صورت P(A) و P(B) در نظر می‌گیریم. برای متغیر C احتمال آن به شرط پدرانش را به صورت P(C|A,B) و برای E و D به صورت P(D|C) و P(E|B,C) در نظر گرفته و حاصلضرب این احتمال‌ها معادل با توزیع توأم متغیرها میشود.
$\mathrm{P(A,\ B,\ C,\ D,\ E)}\mathrm{\ =\ }\mathrm{P}\mathrm{(}\mathrm{A}\mathrm{)}\mathrm{P}\mathrm{(}\mathrm{B}\mathrm{)}\mathrm{P}\mathrm{(}\mathrm{C}\mathrm{|}\mathrm{A}~,\mathrm{B}\mathrm{)}\mathrm{P}\mathrm{(}\mathrm{D}\mathrm{|}\mathrm{C}\mathrm{)}\mathrm{P}\mathrm{(}\mathrm{E}\mathrm{|}\mathrm{C}~,\mathrm{B}\mathrm{)}$
متوسط اگر بدانیم $\mathrm{P}\left(\mathrm{Test}\middle|\mathrm{Disease}\right)=\ \mathrm{0.9}$، $\mathrm{P}\left(\mathrm{\neg Test}\middle|\mathrm{\neg Disease}\right)=\mathrm{0.9}$ و $\mathrm{P}\left(\mathrm{Disease}\right)=\ \mathrm{0.001}$ است، کدام گزینه مقدار تقریبی $\mathrm{P}\left(\mathrm{Disease}\middle|\mathrm{Test}\right)$ را نشان میدهد؟ عدم قطعیت
گزینه 4 صحیح است.
برای محاسبه احتمال خواسته شده طبق قانون بیز داریم :
$\mathrm{P}\mathrm{(}\mathrm{Disease}\mathrm{|}\mathrm{Test}\mathrm{)}\mathrm{\ =\ }\frac{\mathrm{P}\mathrm{(}Test\mathrm{|}\mathrm{Disease}\mathrm{)P(}\mathrm{Disease)}}{\mathrm{P}\mathrm{(}\mathrm{Test}\mathrm{)}}\ =\ \frac{0.9\ \times \ 0.001}{\mathrm{P}\mathrm{(}\mathrm{Test}\mathrm{)}}$
برای محاسبه $P(Test)$ نیز می‌توان از رابطه زیر کمک گرفت :
$\mathrm{P}\mathrm{(}\mathrm{Test}\mathrm{)\ =\ }P(\mathrm{Disease)P}\mathrm{(}Test\mathrm{|}\mathrm{Disease}\mathrm{)\ +\ }P(\neg \mathrm{Disease)P}\mathrm{(}Test\mathrm{|}\neg \mathrm{Disease}\mathrm{)\ =\ 0.001}\times 0.9\ +\ 0.999\ \times 0.1\ $
با جایگذاری مقدار $P(Test)$ در فرمول بالا به عدد تقریبی 0.008 می‌رسیم.
$\mathrm{P}\mathrm{(}\mathrm{Disease}\mathrm{|}\mathrm{Test}\mathrm{)}\mathrm{\ }=\ \frac{0.9\ \times \ 0.001}{\mathrm{0.001}\times 0.9\ +\ 0.999\ \times \ 0.1}\ =\ \frac{9}{9\ +\ 999}\ \simeq \ 0.008$
نمونه سوالات فصل برنامه ریزی درس هوش مصنوعی
دشوار کدام مورد در خصوص مسائل برنامه‌ریزی (Planning)، درست است؟ برنامه ریزی
بررسی گزینه‌ها:
گزینه ۱:
در نظر گرفتن delete listها تضمین نمی‌کند که مسئله بدست آمده را بتوان در زمان چند جمله‌ای حل کرد.
گزینه ۲:
این گزینه صحیح است.
گزینه ۳:
الگوریتم POP از آخرین اهدافی که می‌خواهیم به آنها برسیم شروع میکند و اعمال را از آخر به اول براساس آنها می‌چیند و اگر عملی به پیش‌شرطی نیاز داشت که هنوز مهیا نشده است آن پیش‌شرط را در لیست اهداف می‌گذارد این الگوریتم تا جایی ادامه می‌یابد که پیش شرطی (هدفی) در لیست باقی نمانده باشد.
این الگوریتم جلورو نمی‌باشد و از اهداف شروع میکند بنابراین این گزینه غلط است.
گزینه ۴:
خیر تابع ابتکاری می‌تواند admissible نباشد. برای مثال تصور کنید در یک مسئله ۲ گزاره هدف تولید نشده داریم که با یک عمل با هزینه ۱ تولید می‌شوند. در اینجا تابع ابتکاری h در نظر گرفته شده هزینه ۲ میدهد در حالیکه فاصله واقعی تا هدف h* برابر ۱ است، بنابراین h>h* در نتیجه h قابل قبول نیست.
