در این صفحه نمونه سوالات الکترونیک دیجیتال با پاسخ تشریحی برای شما عزیزان قرار داده شده است، سعی شده مثال های الکترونیک دیجیتال تمامی مباحث را در بر گیرد. در صورتی که علاقه دارید تا بیشتر با درس الکترونیک دیجیتال آشنا شوید و فیلم های رایگان الکترونیک دیجیتال را مشاهده کنید به صفحه معرفی و بررسی الکترونیک دیجیتالمعرفی درس الکترونیک دیجیتال درس الکترونیک دیجیتال در تمامی دانشگاههای جهان به منظور آشنایی با مبانی الکترونیک و سختافزار و تکنولوژیهای استفاده شده از زمان پیدایش کامپیوتر تا کنون تدریس میشود مراجعه کنید.
درس الکترونیک دیجیتال در تمامی دانشگاههای جهان به منظور آشنایی با مبانی الکترونیک و سختافزار و تکنولوژیهای استفاده شده از زمان پیدایش کامپیوتر تا کنون تدریس میشود مراجعه کنید.
قبل از اینکه به ادامه این مقاله بپردازیم توصیه میکنیم که فیلم زیر که در خصوص تحلیل و بررسی درس الکترونیک دیجیتال است را مشاهده کنید، در این فیلم توضیح داده شده که فیلم درس الکترونیک دیجیتال برای چه افرادی مناسب است و همین طور در خصوص فصول مختلف درس الکترونیک دیجیتال و اهمیت هر کدام از فصول آن صحبت شده است.
در ادامه این مقاله ابتدا فیلم های رایگان الکترونیک دیجیتال که به آنها نیاز دارید و سپس نمونه سوالات الکترونیک دیجیتال در اختیارتان قرار گرفته است.
فیلم های رایگان آموزش الکترونیک دیجیتال که به آنها نیاز دارید
در حال حاضر فیلم آموزش الکترونیک دیجیتال استاد رضوی پرطرفدارترین و پرفروشترین فیلم آموزشی الکترونیک دیجیتال کشور است و هر سال اکثر داوطلبان کنکور ارشد کامپیوتر این فیلم را تهیه میکنند.

الکترونیک دیجیتال جلسه 1

الکترونیک دیجیتال جلسه 2

الکترونیک دیجیتال جلسه 3

الکترونیک دیجیتال جلسه 4

نکته و تست الکترونیک دیجیتال جلسه 1

پاسخ تشریحی الکترونیک دیجیتال 1403
خرید فیلم های کامل الکترونیک دیجیتال

فیلم درس الکترونیک دیجیتال
۳۰٪ تخفیف تا ۵ اردیبهشت
1,300,000 تومان
910,000 تومان
رامین رضوی
40 ساعت

فیلم نکته و تست الکترونیک دیجیتال
۳۰٪ تخفیف تا ۵ اردیبهشت
1,040,000 تومان
728,000 تومان
رامین رضوی
25 ساعت
دشوار ظرفیت خازن یک گره در یک مداری که در منطق CMOS طراحی شده است، (PF)0/04 است. اگر ولتاژ کاری مدار 5 ولت باشد و حداکثر افت ولتاژ مجاز برای خازنهای موجود در مدار 5% باشد، با فرض این که جریان نشتی دراین تکنولوژی یک نانو آمپر باشد، حداقل فرکانس بروزرسانی این گره بر حسب KHZ چقدر باید باشد؟ توان ایستا و پویا ، مشخصه های ولتاژ و جریان حواشی نویز
1 200
2100
3 50
4قابل محاسبه نمیباشد.
گزینه 2 صحیح است.
ابتدا بار ذخیره شده در خازن را زمانی که تا 5 ولت شارژ شده است محاسبه میکنیم. داریم:
13- 10 × 2 = 5 ×12- 10 × 04/0 = Q = CV
با توجه این که این بار حداکثر 5% میتواند افت کند پس حداکثر مقدار افت برابر است با:
14- 10 = 13- 10 × 2× 0/05 = حداکثر افت بار خازن
با توجه به رابطه Q=TI که در آن Q بار خازن، I جریان نشتی و T مدت زمان را محاسبه میکند، داریم:
$T\mathrm{=}\frac{Q}{I}\mathrm{=}\frac{{\mathrm{10}}^{\mathrm{-}\mathrm{14}}}{{\mathrm{10}}^{\mathrm{-}\mathrm{9}}}\mathrm{=}{\mathrm{10}}^{\mathrm{-}\mathrm{5}}\mathrm{\Rightarrow }f\mathrm{=}\frac{\mathrm{1}}{T}\mathrm{=}\frac{\mathrm{1}}{{\mathrm{10}}^{\mathrm{-}\mathrm{5}}}\mathrm{=}{\mathrm{10}}^{\mathrm{5}}\mathrm{=}\mathrm{100}\mathrm{(KHz)}$
آسان یک تراشه با فرکانس 400MHz و ولتاژ (V)۵ کار میکند و مصرف توان کل آن 1000 mw است. اگر مصرف توان ایستا (mw) ۲۰۰ باشد و فرکانس کاری تراشه را به (MHz)۲۰۰ ولتاژ را به(V) 2/5 کاهش دهیم، مصرف توان چه مقدار خواهد شد؟ توان ایستا و پویا ، مشخصه های ولتاژ و جریان حواشی نویز
1 100
2300
3 200
4400
گزینه 2 صحیح است.
$P_{\text{پویا}}\mathrm{=}\mathrm{1000}\mathrm{-}\mathrm{200}\mathrm{=}\mathrm{800}\mathrm{(mw)}\mathrm{\ }\text{اولیه}\mathrm{\ }\mathrm{P=}P_{\text{ایستا}}{\mathrm{+}P}_{\text{پویا}}\mathrm{\Rightarrow }\text{کل}$
${\mathrm{\Rightarrow }P}_{\text{پویا}}\mathrm{\times }{\mathrm{(}\frac{\mathrm{2/5}}{\mathrm{5}}\mathrm{)}}^{\mathrm{2}}\mathrm{\times }\frac{\mathrm{200}}{\mathrm{400}}\mathrm{=}\mathrm{800}\mathrm{\times }{\frac{\mathrm{1}}{\mathrm{8}}\mathrm{+}\text{اولیه}\mathrm{\ }P}_{\text{پویا}}\mathrm{=}\text{ثانویه}$
$\mathrm{\Rightarrow }\mathrm{200}\mathrm{+}\mathrm{1}00\mathrm{=}\mathrm{300}P_{\text{کل}}\mathrm{=}\text{جدید}$
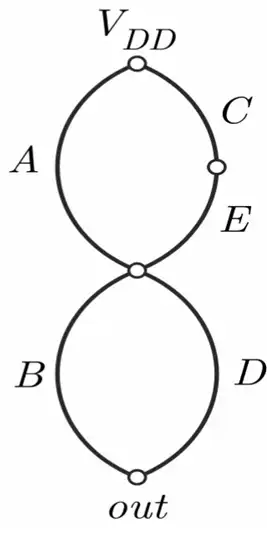
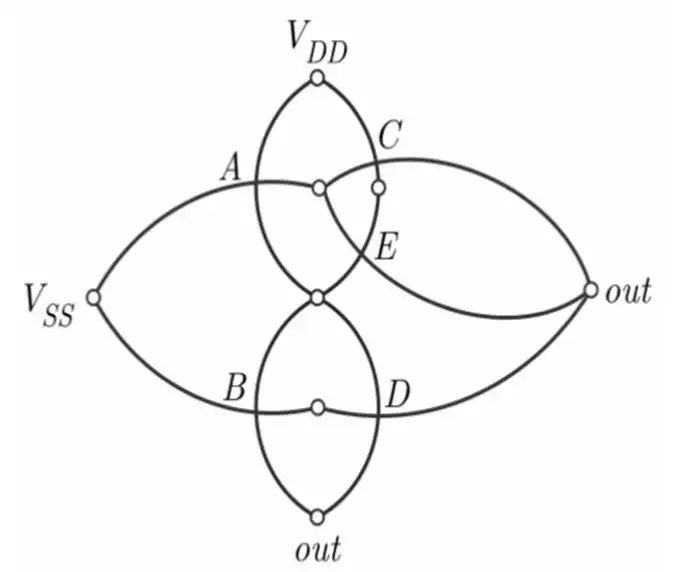
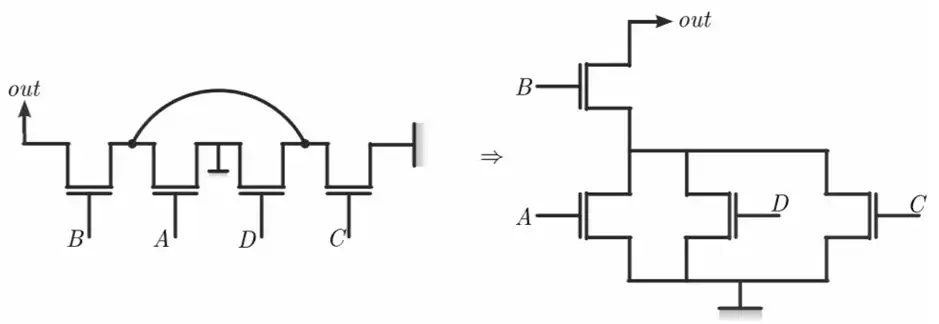
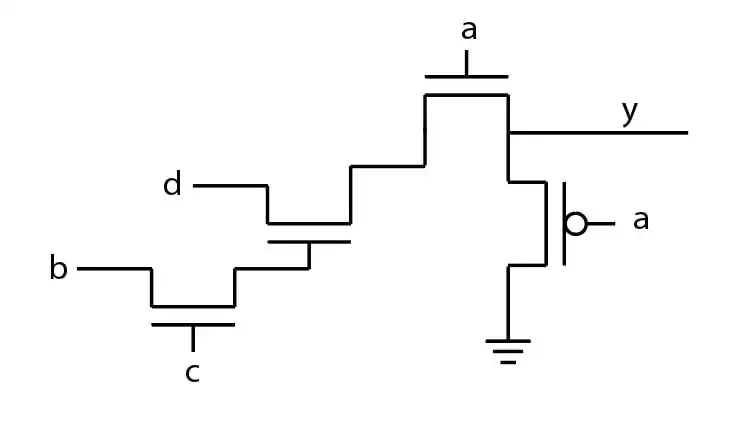
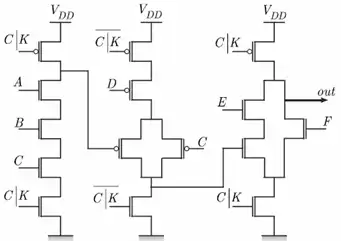
آسان اگر گراف اویلری شبکه pmos یک مدار به صورت مقابل باشد، عبارت منطقی آن کدام است؟
توان ایستا و پویا ، مشخصه های ولتاژ و جریان حواشی نویز
1$out=(A+CE)(B+D)$
2$out\mathrm{=}\overline{\left(A\mathrm{+}CE\right)\left(B\mathrm{+}D\right)}$
3 $out=A⋅(C+E)+BD$
4$out\mathrm{=}\overline{A\mathrm{\cdot }\left(C\mathrm{+}E\right)\mathrm{+}BD}$
گزینه ۴ صحیح است.
بهترین راه حل این است که گراف معادل nmos آن را رسم کرده و از روی آن تابع را بدست آوریم. برای این کار داریم:
توجه کنید اگر بخواهید از روی شبکه pmos بدست آورید باید not ورودی ها را در نظر بگیرید.
آسان یک مدار مجتمع دیجیتال CMOS با تکنولوژی 90 nm با منبع تغذیه 1.8 V ولت کار میکند. کل توان مصرفی این مدار با فرکانس 6.2 ،400 MHz ،clock وات و با فرکانس 600 MHz ،Clock معادل 7.8 وات میباشد. در صورتی که فرکانس Clock به میزان 800 MHz افزایش یابد، میزان توان مصرفی کل مدار چقدر است؟ توان ایستا و پویا ، مشخصه های ولتاژ و جریان حواشی نویز
1 8.6 Watt
29.4 Watt
3 10.8 Watt
412 Watt
گزینه 2 صحیح است.
توان مصرفی مدار شامل دو بخش توان استاتیک و توان دینامیک است. توان دینامیک با فرکانس نسبت مستقیم دارد، اما توان استاتیک با تغییرات فرکانس ثابت است. بنابراین میتوان نوشت:
${\mathrm{P}}_{\text{کل}}\mathrm{=}{\mathrm{P}}_{\text{استاتیک}}\mathrm{+}{\mathrm{P}}_{\text{دینامیک}}\mathrm{\ .\ }{\mathrm{P}}_{\text{دینامیک}}\mathrm{=}\mathrm{Kf}$
$\mathrm{f\ =\ }\mathrm{200}\mathrm{\ MHz\ :\ }\mathrm{6.2}\mathrm{\ Watt\ =\ }{\mathrm{P}}_{\text{استاتیک}}\mathrm{+}\mathrm{K}\mathrm{\times }\mathrm{400}$
$\mathrm{f\ =\ }\mathrm{500}\mathrm{\ MHz\ :\ }\mathrm{7.8}\mathrm{\ Watt\ =\ }{\mathrm{P}}_{\text{استاتیک}}\mathrm{+}\mathrm{K}\mathrm{\times }\mathrm{600}$
از این دو معادله میتوان دو مجهول را به دست آورد:
$\mathrm{K\ =\ }\mathrm{0.008}\mathrm{\ \ .\ \ }{\mathrm{P}}_{\text{استاتیک}}\mathrm{=}\mathrm{3}\mathrm{\ Watt}$
بنابراین در فرکانس 800 MHz میزان توان کل مصرفی این مدار 9.4 Watt خواهد بود.
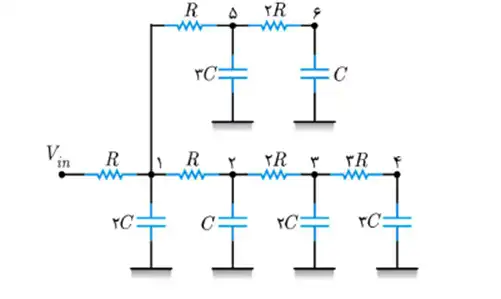
دشوار در شبکه زیر با توجه به مقادیر داده شده بیشینه انحراف کلاک بین نقطه ورودی کلاک و نقاط D,C,B,A چند پیکو ثانیه است؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
$R_{\mathrm{1}}\mathrm{=}R_{\mathrm{2}}\mathrm{=}R_{\mathrm{3}}\mathrm{=}R_{\mathrm{5}}\mathrm{=}R_{\mathrm{6}}\mathrm{=}R_{\mathrm{7}}\mathrm{=}R_{\mathrm{10}}\mathrm{=2(}\mathrm{\Omega }\mathrm{)}$
$R_{\mathrm{4}}\mathrm{=10(}\mathrm{\Omega }\mathrm{)}$
$R_{\mathrm{8}}\mathrm{=5(}\mathrm{\Omega }\mathrm{)}$
$R_{\mathrm{9}}\mathrm{=3(}\mathrm{\Omega }\mathrm{)}$
$C_{\mathrm{1}}\mathrm{=}C_{\mathrm{2}}\mathrm{=}C_{\mathrm{3}}\mathrm{=}C_{\mathrm{5}}\mathrm{=}C_{\mathrm{7}}\mathrm{=}C_{\mathrm{9}}\mathrm{=10(}fF\mathrm{)}$
$C_{\mathrm{4}}\mathrm{=}C_{\mathrm{6}}\mathrm{=}C_{\mathrm{8}}\mathrm{=}C_{\mathrm{10}}\mathrm{=100(}fF\mathrm{)}$
1 2/13
23/7
3 3/64
43/67
گزینه 2 صحیح است.
برای حل این تست با استفاده از تاخیر المور باید تاخیر در هر کدام از نقاط D,C,B,A را بدست آوریم. این تاخیر نسبت به نقطه ورودی است و بدیهی است که بزرگترین مقدار جواب تست خواهد بود.
${\gamma }_A\mathrm{=2\times 10+4\times 10+6\times 10+8\times 10+10\times 100+6\times (100+10+100+10+100)=3120(}fs\mathrm{)}$
${\gamma }_B\mathrm{=2\times 10+4\times 10+6\times 10+16\times 100+6\times (10+100+10+100+10+100)=3700(}fs\mathrm{)}$
${\gamma }_C\mathrm{=2\times 10+4\times 10+6\times 10+13\times 100+6\times (10+100+100)+8(10+100)=3640(}fs\mathrm{)}$
${\gamma }_D\mathrm{=2\times 10+4\times 10+6\times 10+8\times 10+11\times 10+13\times 100+}\mathrm{6\times (10+100+100)+8\times 100=3670(}fs\mathrm{)}$
$\mathrm{\Rightarrow }max\mathrm{=3700(}fs\mathrm{)=3/7(}ps\mathrm{)}$
اگر بیشترین انحراف بین نقاط D,C,B,A را خواسته بود باید حداکثر مقدار را ازحداقل آن کم می کردیم.
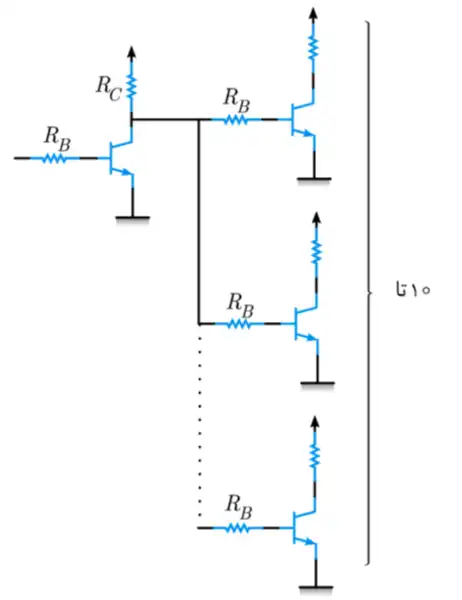
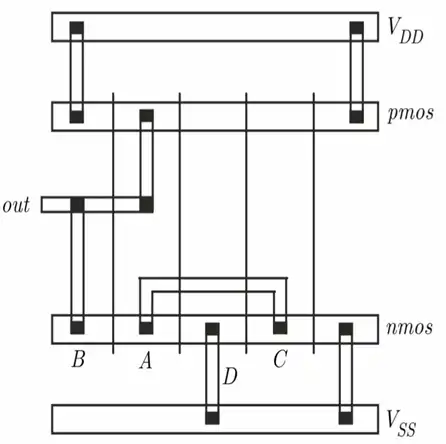
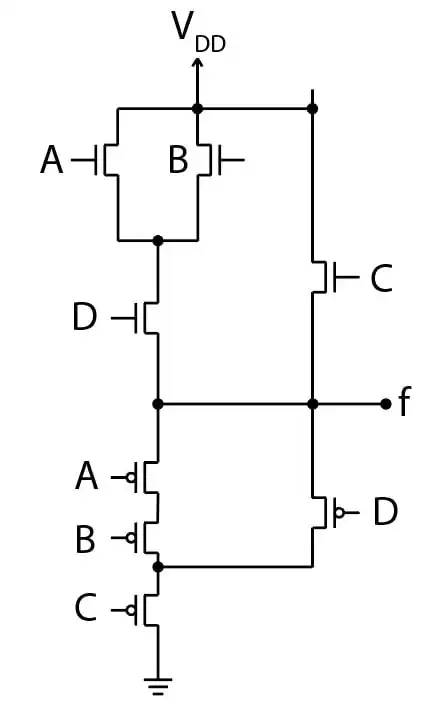
دشوار عبارت منطقی نمودار میله ای روبرو کدام است؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
1 $out\mathrm{=}\overline{A\mathrm{\cdot }\mathrm{(}B\mathrm{+}C\mathrm{+}D\mathrm{)}}$
2$out\mathrm{=}\overline{B\mathrm{\cdot }\mathrm{(}A\mathrm{+}C\mathrm{+}D\mathrm{)}}$
3$out\mathrm{=}A\mathrm{\cdot }\mathrm{(}B\mathrm{+}C\mathrm{+}D\mathrm{)}$
4$out\mathrm{=}\overline{A\mathrm{+ }BCD}$
گزینه ۲ صحیح است.
مدار معادل شبکه pull-down به صورت زیر است:
$out\mathrm{=}\overline{B\mathrm{\cdot }\left(A\mathrm{+}C\mathrm{+}D\right)}$
متوسط در مدار شکل زیر نسبت $\frac{W}{L}$ ترانزیستور شبکه pull-up به ترانزیستور شبکه pull-down چقدر باشد تا مقدار متقارن باشد؟ (فرض کنید از اثر بدنه صرفنظر شده است).
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
1 $4$
2$\frac{1}{4}$
3 $\frac{4}{9}$
4$2/25$
گزینه 3 صحیح است.
در مدار متقارن $V_M= \frac{V_{DD}}{2}$ است یعنی باید $V_M=2/5$ باشد. $V_M$ یعنی مقدار ورودی و خروجی یکسان باشد. در این حالت هر دو ترانزیستور در ناحیه اشباع هستند. فقط توجه کنید که برای ترانزیستور pull-up،
$V_t=-2/7$ است چون ترانزیستور از نوع کاهشی است.
$\mathrm{\Rightarrow }\frac{K'_n}{\mathrm{2}}{\mathrm{(}\frac{W}{L}\mathrm{)}}_{P.U.}{{\mathrm{(}V}_{{GS}_{{\mathrm{(}P.u\mathrm{.)}}_{\mathrm{\circ }}}}\mathrm{-}V_{t_{{\mathrm{(}P.u\mathrm{.)}}_{\mathrm{-}\mathrm{2/7}}}}\mathrm{)}}^{\mathrm{2}}\mathrm{=}\frac{K'_n}{\mathrm{2}}{\mathrm{(}\frac{W}{L}\mathrm{)}}_{P.D.}{{\mathrm{(}V}_{{GS}_{{\mathrm{(}P.D\mathrm{.)}}_{V_{in}\mathrm{=}V_M\mathrm{=}\mathrm{2/5}}}}\mathrm{-}V_{t_{{\mathrm{(}P.D\mathrm{.)}}_{\mathrm{0/7}}}}\mathrm{)}}^{\mathrm{2}}$
$\mathrm{\Rightarrow }\frac{{\mathrm{(}\frac{W}{L}\mathrm{)}}_{P.U.}}{{\mathrm{(}\frac{W}{L}\mathrm{)}}_{P.D.}}\mathrm{=}{\mathrm{(}\frac{\mathrm{2/5}\mathrm{-}\mathrm{0/7}}{\mathrm{2/7}}\mathrm{)}}^{\mathrm{2}}\mathrm{=}{\mathrm{(}\frac{\mathrm{1/8}}{\mathrm{2/7}}\mathrm{)}}^{\mathrm{2}}\mathrm{=}{\mathrm{(}\frac{\mathrm{2}}{\mathrm{3}}\mathrm{)}}^{\mathrm{2}}\mathrm{=}\frac{\mathrm{4}}{\mathrm{9}}$
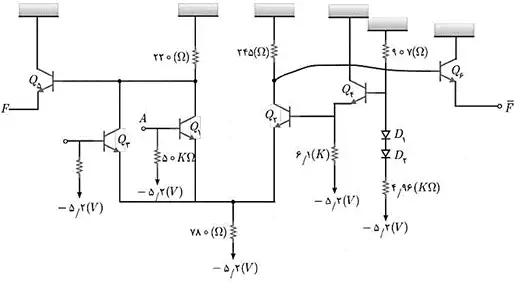
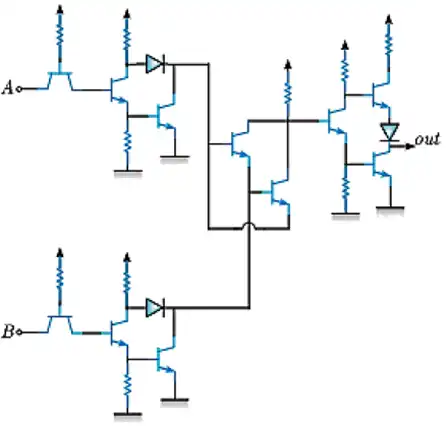
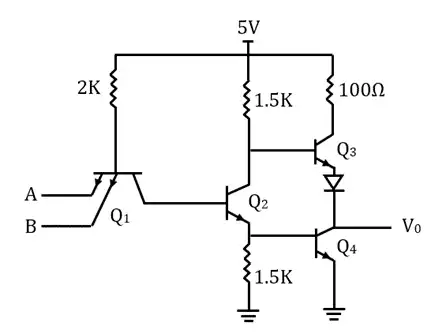
متوسط تابع F در مدار شکل زیر که با منطق ECL رسم شده است پیادهسازی کدام گیت دو ورودی است؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
1 AND
2OR
3 NOR
4NAND
گزینه 3 صحیح است.
قسمتی از مدار که ورودی $Q_2$ میشود برای درست کردن $V_R$ است. پس در واقع با آن کاری نداریم. یک ولتاژ آماده میشود و به بیس $Q_2$ وارد میشود. به همین دلیل در واقع $Q_2$ به عنوان ترانزیستور مرجع در نظر گرفته میشود. ترانزیستورهای $Q_1$ و $Q_3$ ورودی هستند. یعنی در واقع کلید جریان دارای 2 ورودی است. ترانزیستورهای $Q_5$ و $Q_6$ نیز خروجی را تأمین میکنند.
اگر هر یک از ورودیهای A یا high ،B باشد ترانزیستور $Q_1$ یا $Q_3$ روشن شده و در نتیجه $Q_2$ خاموش میشود. در نتیجه خروجی high ،$Q_6$ میشود و خروجی low ،$Q_5$. پس:
$F=\overline{A+B}\ \ , \ \ \overline{F}=A+B$
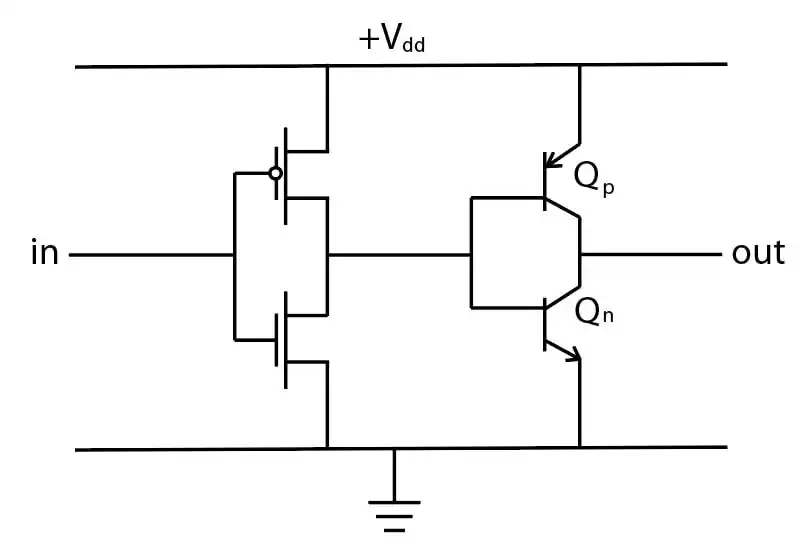
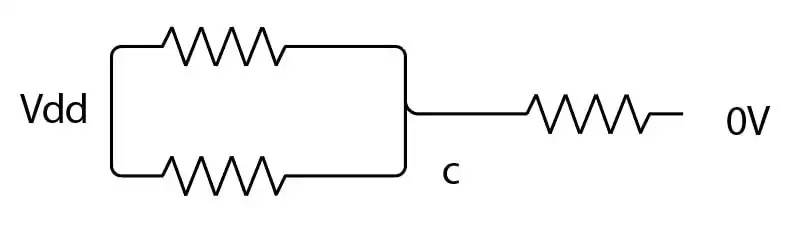
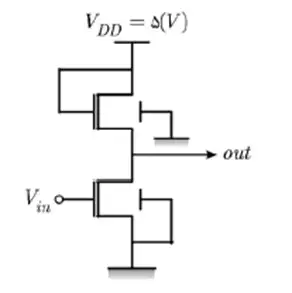
آسان سطوح ولتاژ خروجی صفر منطقی و یک منطقی چقدر میباشند؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
1$ V_{dd}-V_{CE(Sat)},V_{be}$
2$V_{dd}-V_{be},V_{CE(Sat)}$
3 $V_{dd}-V_{CE(Sat)},V_{CE(Sat)}$
4سطوح منطقی قابل قبول نمیدهد.
گزینه 4 صحیح است.
به مدار ترانزیستورها لازم نیست توجه کنید فقط کافیست به BJTها دقت کنید.
فرض کنید ورودی سر بیس ترانزیستورها ۱ منطقی (ولتاژ بالا) است. اگر چنین باشد ابتدا $Q_n$ روشن میشود و با روشن شدن آن چون میدانیم $V_{BE}=0.7V$ در حالت روشن است جریان از این BJT عبور کرده و ولتاژ بیس کاهش مییابد با کاهش آن $Q_p$ روشن میشود و جریان عبوری از $Q_n$ را جبران میکند در نتیجه بیس ولتاژی میان صفر و یک منطقی میگیرد که بستگی به مشخصات ترانزیستورها دارد.
وضعیت سر کالکتور ترانزیستورها در این موقعیت نیز مشابه است، چون هر دو ترانزیستور BJT روشن هستند ولتاژ کاکلتور ولتاژی نامشخص میان صفر و یک منطقی میگیرد که بستگی به مشخصات ترانزیستورها دارد. بنابراین سطح ولتاژ قابلقبولی خروجی ندارد.
اگر ورودی سر بیس ترانزیستورها در ابتدا صفر منطقی (ولتاژ پایین) باشد، وضعیتی مشابه وضعیت بالا رخ میدهد با این تفاوت که در اینجا ابتدا $Q_p$ روشن میشود.
در کل ولتاژ خروجی سطح قابل قبولی ندارد.
متوسط در مدار شکل زیر نسبت تأخیر گره 3 به گره 5 کدام است؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
1 $\frac{4}{7}$
2$\frac{7}{4}$
3 $2$
4$\frac{1}{2}$
گزینه 2 صحیح است.
برای حل این تست باید از تأخیر المور شبکه درختی RC استفاده کنید چون از ورودی به گره فقط یک راه وجود دارد، پس داریم:
${\tau }_{\mathrm{3}}\mathrm{=}R\mathrm{(}\mathrm{2}C\mathrm{)+(}R\mathrm{+}R\mathrm{)(}C\mathrm{)+(}R\mathrm{+}R\mathrm{+}\mathrm{2}R\mathrm{)(}\mathrm{2}C\mathrm{)+(}R\mathrm{+}R\mathrm{+}\mathrm{2}R\mathrm{)(}\mathrm{3}C\mathrm{)+}R\mathrm{(}\mathrm{3}C\mathrm{)+}R\mathrm{(}C\mathrm{)}$
$\mathrm{\ }\mathrm{\ \ \ \ \ =}\mathrm{2}\mathrm{R}C\mathrm{+}\mathrm{2}\mathrm{R}C\mathrm{+}\mathrm{8}\mathrm{R}C\mathrm{+}\mathrm{12}\mathrm{R}C\mathrm{+}\mathrm{3}\mathrm{R}C\mathrm{+}\mathrm{R}C\mathrm{=}\mathrm{28}\mathrm{R}C$
${\tau }_{\mathrm{5}}\mathrm{=}R\mathrm{(}\mathrm{2}C\mathrm{)+}R\mathrm{(}C\mathrm{)+}R\mathrm{(}\mathrm{2}C\mathrm{)+}R\mathrm{(}\mathrm{3}C\mathrm{)+(}R\mathrm{+}R\mathrm{)(}\mathrm{3}C\mathrm{)+(}R\mathrm{+}R\mathrm{)(}C\mathrm{)}$
$\mathrm{\ \ \ \ \ =}\mathrm{2}\mathrm{R}C\mathrm{+}\mathrm{R}C\mathrm{+}\mathrm{2}\mathrm{R}C\mathrm{+}\mathrm{3}\mathrm{R}C\mathrm{+}\mathrm{6}\mathrm{R}C\mathrm{+}\mathrm{2}\mathrm{R}C\mathrm{=}\mathrm{16}\mathrm{R}C$
$\mathrm{\Rightarrow }\frac{{\tau }_{\mathrm{3}}}{{\tau }_{\mathrm{5}}}\mathrm{=}\frac{\mathrm{28}}{\mathrm{16}}\mathrm{=}\frac{\mathrm{7}}{\mathrm{4}}$
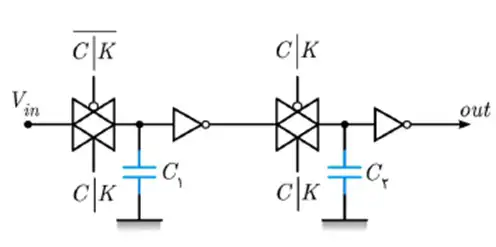
آسان مدار شکل زیر پیادهسازی چه نوع عنصر حافظه است؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
1یک D-FF حساس به سطح مثبت
2یک D-FF حساس به سطح منفی
3 یک D-FF حساس به لبه پایین رونده
4یک D-FF حساس به لبه بالا رونده
گزینه 3 صحیح است.
یکی از روشهایی که FFهای حساس به لبه را طراحی میکنند روشهای master – slage است. در این روشها دو لچ حساس به سطح مثبت و منفی را در ادامه هم میبندند. در صورتی که لچ اول حساس به سطح مثبت باشد (یعنی با ۱ = C|K فعال باشد)، FF حاصل حساس به لبه پایین رونده و در غیر این صورت حساس به لبه بالارونده میشود.
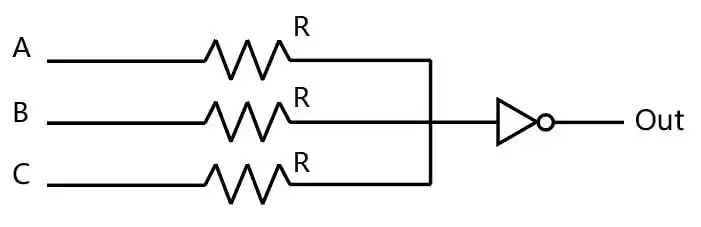
آسان به فرض آنکه معکوس کننده ایدهآل با ولتاژ آستانه $\frac{V_{DD}}{2}$ است، مدار چه تابعی را پیادهسازی میکند؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
1$\overline{AB+AC+BC}$
2${AB+AC+BC}$
3NOR سه ورودی
4NAND سه ورودی
گزینه 1 صحیح است.
وقتی ۳ ورودی صفر باشد $V_c$(ولتاژ نقطه میان مقاومتها و معکوس کننده) برابر صفر میشود در نتیجه خروجی یک میشود.
وقتی ۳ ورودی یک باشد $V_c$ برابر یک میشود در نتیجه خروجی صفر میشود.
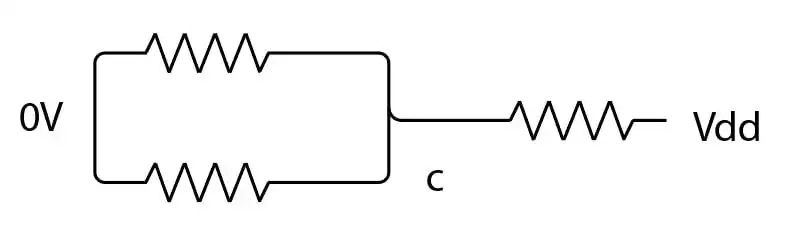
اگر دو تا از ورودیها صفر و یکی از آنها یک باشد مدار زیر را داریم:
$V_c=\frac{\frac{R}{2}}{R+\frac{R}{2}}\times V_{dd}=\frac{1}{3}\times V_{dd}<\frac{V_{dd}}{2}$
ولتاژ بدست آمده کمتر از ولتاژ آستانه است در نتیجه ورودی معکوس کننده صفر تلقی شده و خروجی یک میشود.
اگر دو تا از ورودیها یک و یکی از آنها صفر باشد مدار زیر را داریم:
$V_c=\frac{R}{R+\frac{R}{2}}\times V_{dd}=\frac{2}{3}\times V_{dd}>\frac{V_{dd}}{2}$
ولتاژ بدست آمده بیشتر از ولتاژ آستانه است در نتیجه ورودی معکوس کننده یک تلقی شده و خروجی صفر میشود.
خلاصه بالا:
اگر حداقل دو تا از ورودیها یک باشد خروجی صفر میشود در غیر این صورت خروجی یک است.
با توجه به این موارد گزینه صحیح گزینه ۱ است:
$\overline{AB+AC+BC}$
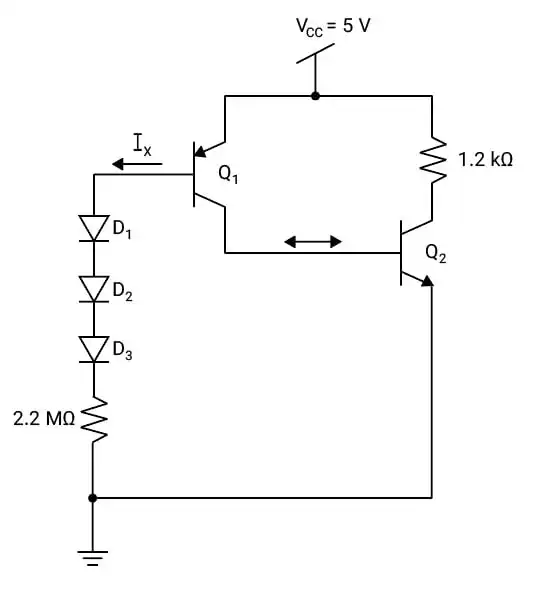
متوسط برای مدار نشان داده شده در شکل زیر فرض کنید هر دو ترانزیستور دارای $\beta=25$ باشند. همچنین دیودهای $D_2 \ ،D_1$ و $D_3$ مشابه فرض میشوند. جریان $I_X$ چهقدر است؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
1$1.5\mu A$
2$1\mu A$
3$2\mu A$
4$0 \mu A$
گزینه 2 صحیح است.
فرض کنید $Q_1$ و $Q_2$ هر دو روشن و در حالت بایاس مستقیم قرار دارند:
$→V_{B1}=5-V_{BE-on}=5-0.7=4.3V$
$V_{R_{2.2}}=V_{B1}-3V_D=4.3-3×0.7=2.2V$
$I_x=\frac {V_{R_{2.2}}}{R_{2.2}} =\frac {2.2}{2.2MΩ}=1 μA$
حال باید بررسی کنیم آیا واقعا $Q_1$ روشن بوده و در حالت بایاس مستقیم است:
$V_{C1}=V_{B2}=0.7V\to V_{CE1}=5-0.7=4.3>V_{CEsat}\to \ \text{بایاس }\\ \text{مستقیم }\ Q_1$
$I_{C1}=I_{B2}=βI_{B1}=βI_x=25×1μA=25 μA$
$I_{C2}=βI_{B2}=25×25μA=625μA$
$V_{C2}=5-R_{1.2}I_{C2}=5-1.2\times 0.625=4.25\to V_{CE2}=4.25V>V_{CEsat}\to \ \text{بایاس }\\ \text{مستقیم } \ Q_2$
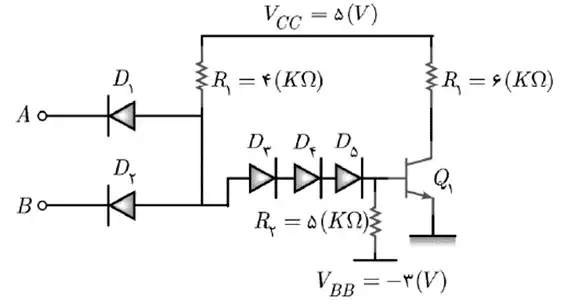
متوسط در مدار شکل زیر، حاشیه نویز بالا کدام است؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
$V_{BE(on)}=\mathrm{0/7}(V)\ ,\ V_{CE(sat)}=\mathrm{0/2}(V)\ ,V_{BE(sat)}=\mathrm{0/8}(V)\ ,\ V_{D(on)}=\mathrm{0/7}(V)$
1$2/8$
2$2/2$
3$2/5$
4$3/5$
گزینه 1 صحیح است.
برای بدست آوردن حاشیه نویز بالا باید $V_{OH}$ و $V_{IH}$ را بدست آوریم. $V_{OH}$ به دلیل قطع بودن طبقه
pull – down و بایاس معکوس دیودها همان $V_{CC}$ میشود. پس $V_{OH}\mathrm{=}V_{CC}\mathrm{=}\mathrm{5}\mathrm{(}V\mathrm{)}$
$V_{IH}$ حداقل ولتاژ ورودی است که خروجی low شود. اگر خروجی low شود ترانزیستور به ناحیه اشباع میرود به همین دلیل برای ولتاژ ورودی داریم:
$V_{IH}=V_{BE(sat)}+\overbrace{{3V}_{D(on)}}^{D_{\mathrm{5}},D_{\mathrm{4}},D_{\mathrm{3}}\text{برای}\ }{-V}_{D(on)}=\mathrm{0/8}\mathrm{+}\mathrm{2/1}-\mathrm{0/7}\mathrm{=}\mathrm{2/2}\mathrm{(V)}$
$\mathrm{\Rightarrow }{NM}_{\mathrm{(}H\mathrm{)}}\mathrm{=}\mathrm{5}\mathrm{-}\mathrm{2/2}\mathrm{=}\mathrm{2/8}$
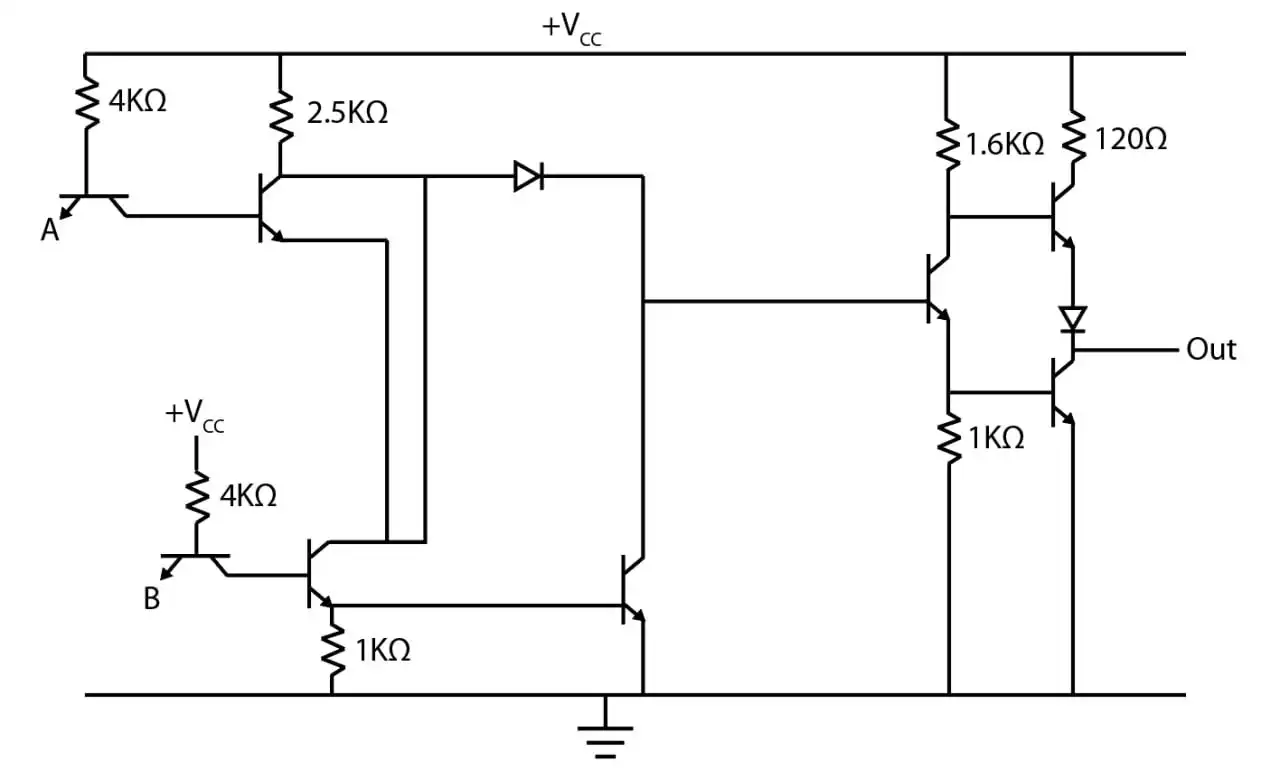
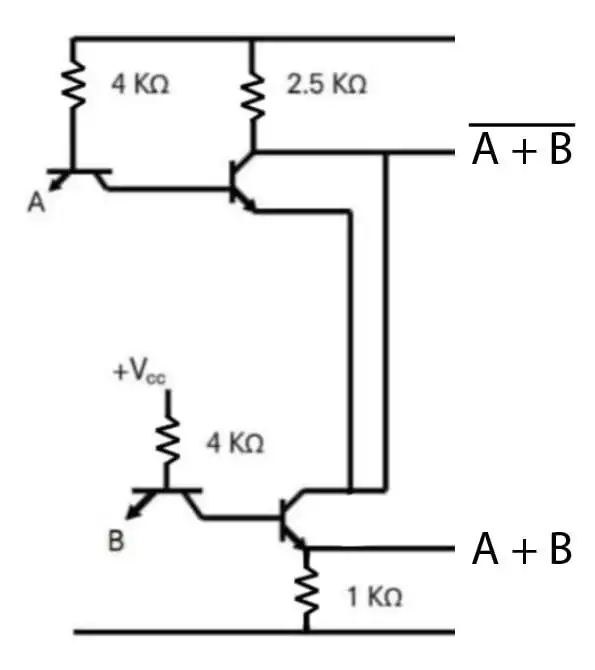
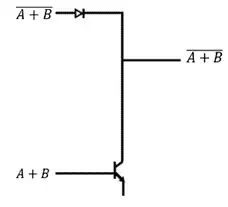
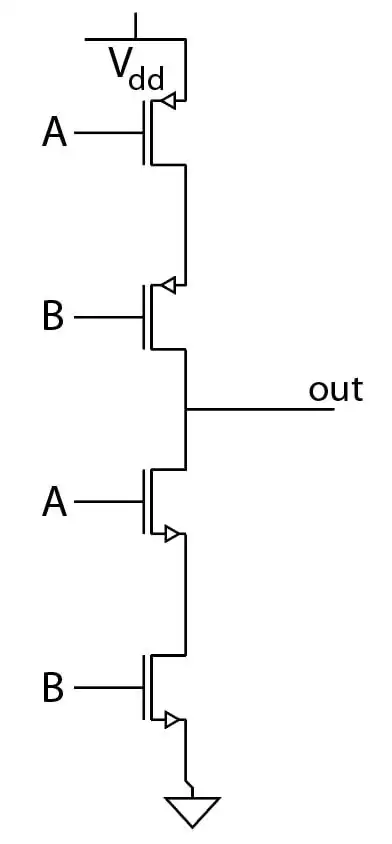
متوسط دروازه نشان داده شده در شکل مقابل چه نوع مدار منطقی میباشد؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
1OR
2NOR
3XOR
4XNOR
در ابتدای مدار دو مدار TTL داریم که خروجی از سمت کالکتور آنها برابر عکس ورودی و خروجی از سمت امیتر برابر خود ورودی است.
چون خروجیهای این دو TTL به هم متصل است اگر هر کدام از ورودیهای یک باشد خروجی بالایی صفر و پایینی یک میشود:
$O_1=A+B,\ O_2=\overline{A+B}$
مدار بعدی یک DTL است که اگر ورودی دیود یک باشد معکوس ورودی بیس ترانزیستور در خروجی میآید در غیر این صورت خروجی برابر صفر:
$O_3=\overline{\left(A+B\right)}.\overline{(A+B)}=\overline{A+B}$
در نهایت به یک مدار معکوس کننده میرسیم:
$out=\overline{\overline{A+B}}=A+B$
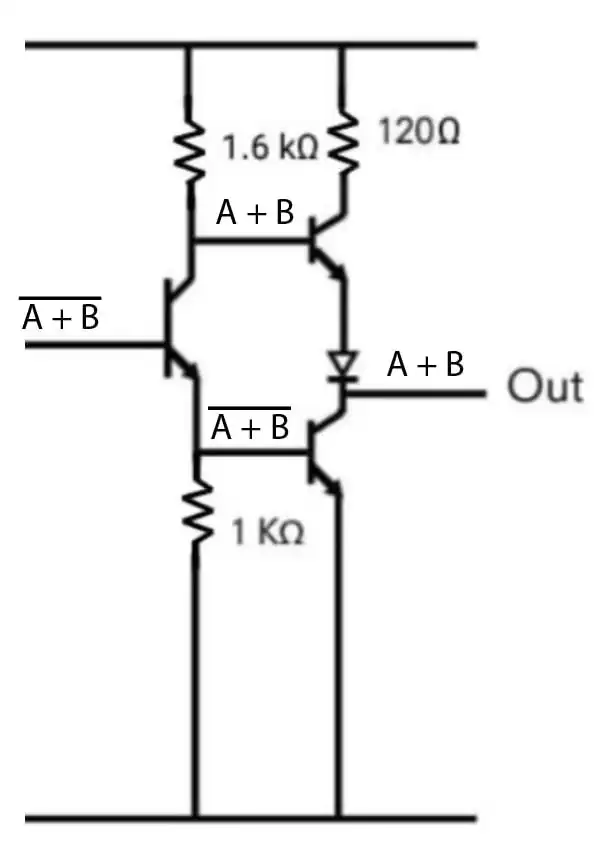
متوسط مدار نشان داده شده در زیر کدام گیت منطقی را نشان می دهد؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
1XNOR
2NOR
3NAND
4XOR
گزینه 4 صحیح است.
در این مدار هرکدام از ورودی ها یک بخش مجزا دارند. ایده اصلی دو ترانزیستور وسط که کلکتور آن ها به هم متصل شده است، می باشد. اگر دقت کنید متوجه می شوید که بیس ترانزیستور بالای از این دو ترانزیستور و امیتر ترانزیستور پایینی در واقع not ورودی A را پیاده سازی می کنند و دقیقا همین اتفاق برای بیس ترانزیستور پایینی و امیتر بالایی می افتد. پس این امکان نیز not ورودی B است.
پس اگر هر دو ورودی مقداری یکسان داشته باشند بیس و امیتر هر دو ترانزیستور یکسان می شود و در نتیجه هر دو خاموش می شود. خاموش شدن این دو باعث 0 شدن شدن خروجی از طریق دو ترانزیستور دیگر میشود. اما اگر ورودی ها یکسان نباشند یکی از دو ترانزیستور وسط روشن می شود و این باعث می شود که ترانزیستور یکی مانده به طبقه آخر خاموش شود و خروجی از طریق pull-up تحریک شود.
دشوار در گیت NAND(TTL) مطابق شکل مقابل، مقادیر جریان ورودی در حالت Low ($I_{IL}$) برحسب میلیآمپر و جریان ورودی در حالت High ($I_{IH}$) برحسب میکروآمپر بهترتیب به کدام گزینه نزدیکتر هستند؟
BJT، دیودها و مدارهای آینه جریان، مدارهای خارنی مقاومتی
$V_{BE}=0.7V$
$V_{CE(sat)}=0.3V$
$\beta _{F}=50,\beta _{R} =0.04$
11 ، 60
22 ، 30
32 ، 60
43 ، 30
گزینه 2 صحیح است.
جریان $I_{IL}$ :
جریان $I_{IL}$ زمانی اتفاق میافتد که یکی از ورودیها صفر و دیگری یک منطقی باشد. در این حالت $Q_1$ روشن است و $Q_2$ خاموش (سر کالکتور ترانزیستور $Q_1=A.B$ است.).
جریان $I_L$ در این شرایط برابر زیر است:
$I_{IL}=\frac{V_{dd}-V_{BEon}-V_{inL}}{R_{2k}}$
ولتاژ $V_{inL}$ ولتاژ صفر منطقی ورودیها میباشد، این مقدار براساس مدار قبلی از مدار فعلی تعیین میشود. در اینجا ابتدا فرض کنید این مقدار صفر است، در نتیجه داریم:
$I_{IL}=\frac{5-0.7}{2}=2.15\ mA$
اگر مدار قبل از مدار فعلی از نوع ttl باشد $V_{inL}=V_{CE(sat)}=0.3$ است در نتیجه:
$I_{IL}=\frac{5-0.7-0.3}{2}=2mA$
جریان بدست آمده بیشترین مقدار جریانی است که از مدار فعلی به داخل ورودی و مدار قبلی میرود. اگر دو ورودی صفر باشند جریانی که از مدار به ورودی میرود کمتر است بنابراین $I_{IL}$ نیست.
جریان $I_{IH}$ :
این جریان در زمانی اتفاق میافتد که هر دو ورودی یک منطقی باشند.
آنگاه ترانزیستورهای $Q_2,Q_4$ روشن و $Q_1$ خاموش میشود. در این شرایط $Q_1$ در حالت فعال معکوس است، زیرا دیود میان بیس و امیتر بایاس معکوس و دیود میان بیس و کالکتور بایاس مستقیم میشود.
وقتی BJT در حالت فعال معکوس است جریان به سر امیتر آن وارد میشود و مقدار آن برابر است با:
$I_E=β_R I_B$
مقدار $I_B$ با توجه به روشن بودن دو ترانزیستور $Q_2,Q_4$ برابر است با:
$I_B=\frac{V_{DD}-V_{BCon1}-V_{BEon2}-V_{BEon4}}{R_{2k}}=\frac{5-0.7-0.7-0.7}{2}=1.45\ mA$
$→I_E=0.04×1.45=58μA$
توجه کنید این جریان از دو ورودی گرفته میشود، اگر بخواهیم برای یک ورودی در نظر بگیریم داریم:
$I_{IH}=\frac{I_E}{2}=\frac{58}{2}=29\mu A\approx 30\mu A$
آسان در مدار شکل زیر بازه تغییرات ولتاژ خروجی کدام مورد است؟
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
1$V_{DD}-V_{tn}$ و $\circ$
2$V_{DD}-2V_{tn}$ و $\circ$
3$V_{DD}-V_{tn}$ و $|V_{tp}|$
4$V_{DD}-2V_{tn}$ و $|V_{tp}|$
گزینه 2 صحیح است.
برای حل این سوال به این نکته توجه کنید:
نکته: اگر ترانزیستورها روشن باشند و جریان به صفر برسد:
در NMOS ولتاژ بالا به طور کامل عبور کرده ولی ولتاژ پایین سمت دیگر برابر $min(V_D,V_G-V_{tn})$ است.
در PMOS اگر سورس ولتاژ پایین داشته باشد درین نیز همان را دارد امّا در صورت وجود ولتاژ بالا سمت دیگر برابر $min(V_S,V_G+|V_{tp}|)$ است.
اگر a صفر باشد PMOS روشن میشود که مطابق نکته بالا صفر زمین به خروجی میرود. بنابراین کمترین مقدار خروجی $0$ است.
تنها زمانی که خروجی میتواند یک باشد زمانی است که ۳ NMOS روشن شوند و d یک باشد. در این شرایط بین b که ولتاژ $V_{dd}$ است تا خروجی دو NMOS وجود دارد. همچنین ورودی گیت یکی از این NMOS از طریق یک NMOS دیگر تامین میشود.
ولتاژ گیت NMOS اول برابر است با:
$V_{g1}={\mathrm{min} \left(V_{dd},\ V_{dd}-V_t\right)\ }=V_{dd}-V_t$
خروجی برابر است با:
$out={\mathrm{min} \left(V_{g2}-V_t,{\mathrm{min} \left(V_{g1}-V_t,\ V_{dd}\right)\ }\right)\ }$
$\to out={\mathrm{min} \left(V_{dd}-V_t,{\mathrm{min} \left(V_{dd}-V_t-V_t,\ V_{dd}\right)\ }\right)\ }$
$\to out={\mathrm{min} \left(V_{dd}-V_t,\ V_{dd}-2V_t\right)\ }=V_{dd}-2V_t\ \ maximum\ output$
دشوار یک وارونگر که خازن ورودی آن برابر 1 است، یک بار خازنی ۲۵۶ را میخواهد درایو کند. اگر بتوانیم به جای یک وارونگر از ۴ وارونگر استفاده کنیم، تاخیر تحریک این بار در بهترین حالت که از ۴ وارونگر استفاده کنیم، نسبت به استفاده از یک وارونگر کدام است؟ $\mathrm{(}{\gamma }_{inv}\mathrm{=}\mathrm{1}\mathrm{)}$ خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
13/4
24
316
412/8
گزینه 4 صحیح است.
همانطور که میدانید در صورتی که از تعداد محدود وارونگر میتوانیم استفاده کنیم باید اندازه خازن هر وارونگر واسط هندسی در وارونگر اطرافش باشد که در نهایت f که مقداری است که در اندازه هر وارونگر ضرب میشود از رابطه زیر بدست میآید:
$f\mathrm{=}\sqrt[N]{\frac{C_{out}}{C_{in}}}\mathrm{\Rightarrow }f\mathrm{=}\sqrt[{\mathrm{4}}]{\mathrm{256}}\mathrm{=}\mathrm{4}$
حال در این صورت تأخیر برابر است با :
${\tau }_{\text{بهینه}}\mathrm{=}N{\tau }_{\mathrm{inv}}\mathrm{(}f\mathrm{+}{\gamma }_{\mathrm{inv}}\mathrm{)=}\mathrm{4}\mathrm{\times }{\tau }_{\mathrm{inv}}\mathrm{(}\mathrm{4}\mathrm{+}\mathrm{1}\mathrm{)=}\mathrm{20}{\tau }_{\mathrm{inv}}$
در حالت اولیه نیز تأخیر برابر $256\tau _{inv}$ است، پس نسبت میشود:
$\frac{\mathrm{256}}{\mathrm{20}}\mathrm{=}\mathrm{12/8}$
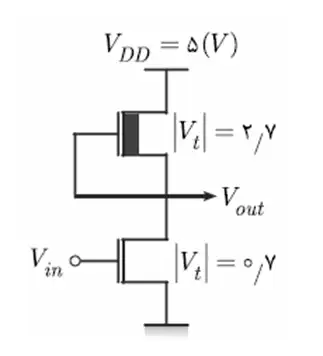
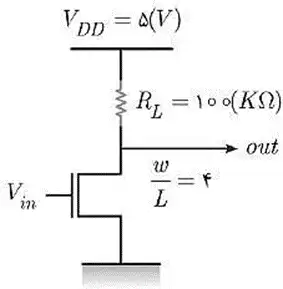
متوسط برای یک معکوسکننده با بار مقاومتی با پارامترهای زیر، $V_M$ کدام است؟
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
$\left(\mu_{\mathrm{n}}{\mathrm{C}}_{\mathrm{OX}}\mathrm{=}\mathrm{50}\left(\frac{µ_{\mathrm{A}}}{{\mathrm{V}}^{\mathrm{2}}}\right)\mathrm{\ ,\ }\frac{\mathrm{w}}{\mathrm{L}}\mathrm{=}\mathrm{4}\mathrm{\ ,\ }{\mathrm{V}}_{\mathrm{T}}\mathrm{=}{\mathrm{1}}^{\left(\mathrm{V}\right)}\mathrm{\ ,\ }{\mathrm{V}}_{\mathrm{DD}}\mathrm{=}{\mathrm{5}}^{\left(\mathrm{V}\right)}\mathrm{\ ,\ }{\mathrm{R}}_{\mathrm{L}}\mathrm{=}{\mathrm{100}}^{\left(\mathrm{K}O\right)}\right)$
10/316
20/527
31/423
41/584
گزینه 4 صحیح است.
معکوسکننده با بار مقاومتی به صورت زیر است:
$V_m$ نقطهای است که در آن ولتاژ ورودی و خروجی با یکدیگر برابر هستند. در این شرایط حتماً ترانزیستور در ناحیه اشباع قرار دارد. با برابر قرار دادن جریان عبوری از ترانزیستور و مقاومت داریم:
$\frac{{\mathrm{V}}_{\mathrm{DD}}\mathrm{-}{\mathrm{V}}_{\mathrm{M}}}{{\mathrm{R}}_{\mathrm{L}}}\mathrm{=}\frac{\mathrm{K}}{\mathrm{2}}{\left({\mathrm{V}}_{\mathrm{m}}\mathrm{-}{\mathrm{V}}_{\mathrm{t}}\right)}^{\mathrm{2}}\mathrm{\Rightarrow }\frac{\mathrm{5}\mathrm{-}{\mathrm{V}}_{\mathrm{M}}}{\mathrm{10}\mathrm{\ \times }{\mathrm{10}}^{\mathrm{3}}}\mathrm{=}\frac{\mathrm{1}}{\mathrm{2}}\mathrm{\times }\mathrm{4}\mathrm{\ \times \ }\mathrm{50}\mathrm{\times \ }{\mathrm{10}}^{\mathrm{-}\mathrm{6}}\left( {\mathrm{V}}_{\mathrm{m}}\mathrm{-}\mathrm{1}\right)$
$\mathrm{\Rightarrow }\mathrm{5}\mathrm{-}{\mathrm{V}}_{\mathrm{M}}\mathrm{=}\mathrm{10}\left( {\mathrm{V}}^{\mathrm{2}}_{\mathrm{m}}\mathrm{-}{\mathrm{2}\mathrm{V}}_{\mathrm{m}}\mathrm{+}\mathrm{1}\right)\mathrm{\Rightarrow }{\mathrm{10}\mathrm{V}}^{\mathrm{2}}_{\mathrm{m}}\mathrm{-}{\mathrm{19}\mathrm{V}}_{\mathrm{m}}\mathrm{+}\mathrm{5}\mathrm{\ =\ }\mathrm{\circ }\mathrm{\ }\mathrm{\Rightarrow }{\mathrm{V}}_{\mathrm{m}}\mathrm{=}\mathrm{584/1}\mathrm{\ \ ,\ \ }\mathrm{36/0}$
ولتاژ $V_m$ باید از $V_t$ یعنی 1 ولت بیشتر باشد تا ترانزیستور روشن شود به همین دلیل 0/316 غیر قابل قبول است.
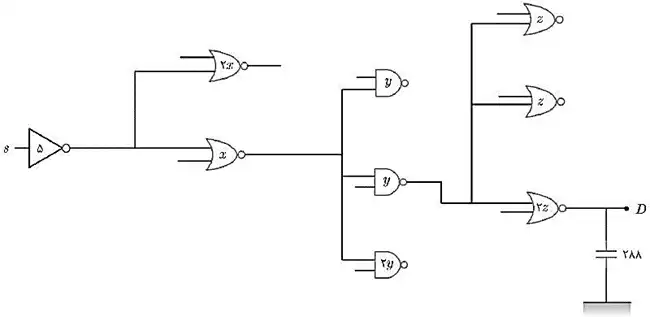
دشوار در مدار شکل زیر، y چه مقداری داشته باشد تا تأخیر از مسیر S به D حداقل
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
18
224
320
413/3
گزینه 3 صحیح است.
ابتدا باید G کل را که از حاصلضرب gها در مسیر به دست میآید را محاسبه کنیم:
$ \ not \ \text{برای }\ \ \Rightarrow \ \ g_1,h_1 $ $\ \ \ \ \ \ \ \ \text{در }\ \text{مسیر }\ NANA \ \text{برای }\ \Rightarrow \ g_3,h_3$
$\mathrm{\Rightarrow }\mathrm{\ \ \ }\mathrm{G\ =\ }{\mathrm{g}}_{\mathrm{1}}\mathrm{\times }{\mathrm{g}}_{\mathrm{2}}\mathrm{\times }{\mathrm{g}}_{\mathrm{3}}\mathrm{\times }{\mathrm{g}}_{\mathrm{4}}\mathrm{=}\mathrm{1}\mathrm{\ \times }\frac{\mathrm{4}}{\mathrm{3}}\mathrm{\times }\frac{\mathrm{5}}{\mathrm{3}}\mathrm{\times }\frac{\mathrm{4}}{\mathrm{3}}\mathrm{=}\frac{\mathrm{80}}{\mathrm{27}}\mathrm{\Rightarrow }$ مقادیر تلاشها را باید حفظ باشید
$\mathrm{H\ =}\frac{{\mathrm{C}}_{\mathrm{L}}}{{\mathrm{C}}_{\mathrm{in}}}\mathrm{=}\frac{\mathrm{288}}{\mathrm{5}}$
$\mathrm{B\ =\ }\Pi\frac{{\mathrm{C}}_{\mathrm{on}\left(\mathrm{path}\right)}\mathrm{+}{\mathrm{C}}_{\mathrm{off}\left(\mathrm{path}\right)}}{{\mathrm{C}}_{\mathrm{on}\left(\mathrm{path}\right)}}\mathrm{=}\frac{\mathrm{x\ +\ }\mathrm{2}\mathrm{x}}{\mathrm{x}}\mathrm{\times }\frac{\mathrm{y\ +\ y\ +\ }\mathrm{2}\mathrm{y}}{\mathrm{y}}\mathrm{\times }\frac{\mathrm{z\ +\ z\ +\ }\mathrm{2}\mathrm{z}}{\mathrm{2}\mathrm{z}}\mathrm{=}\mathrm{3}\mathrm{\ \times \ }\mathrm{4}\mathrm{\ \times \ }\mathrm{2}\mathrm{\ =\ }\mathrm{24}$
$\mathrm{F\ =\ GBH\ =}\frac{\mathrm{80}}{\mathrm{27}}\mathrm{\times }\mathrm{24}\mathrm{\ \times }\frac{\mathrm{288}}{\mathrm{5}}\mathrm{=}\mathrm{16}\mathrm{\ \times \ }\mathrm{8}\mathrm{\ \times \ }\mathrm{32}\mathrm{\ =}{\mathrm{2}}^{\mathrm{4}}\mathrm{\times }{\mathrm{2}}^{\mathrm{3}}\mathrm{\times }{\mathrm{2}}^{\mathrm{5}}\mathrm{=}{\mathrm{2}}^{\mathrm{12}}\mathrm{\ \ \ }\mathrm{\Rightarrow }\mathrm{\ \ \ }\mathrm{f\ =\ }\sqrt[{\mathrm{4}}]{{\mathrm{2}}^{\mathrm{12}}}\mathrm{=}{\mathrm{2}}^{\mathrm{3}}\mathrm{=}\mathrm{8}$
حال باید از آخر شروع کنیم به محاسبه کردن:
$\mathrm{z\ }\text{محاسبه}\mathrm{\ \ \ }\mathrm{\Rightarrow }\mathrm{\ \ \ f\ =}{\mathrm{g}}_{\mathrm{4}}{\mathrm{h}}_{\mathrm{4}}\mathrm{\ \ \ }\mathrm{\Rightarrow }\mathrm{\ \ \ }\mathrm{8}\mathrm{\ =\ }\frac{\mathrm{4}}{\mathrm{3}}\mathrm{\times }\frac{\mathrm{288}}{\mathrm{2}\mathrm{z}}\mathrm{\ }\mathrm{\Rightarrow }\mathrm{z\ =\ }\frac{\mathrm{4}\mathrm{\ \times \ }\mathrm{288}}{\mathrm{6}\mathrm{\ \times \ }\mathrm{8}}\mathrm{=}\mathrm{24}$
$\mathrm{y\ }\text{محاسبه}\mathrm{\ \ \ }\mathrm{\Rightarrow }\mathrm{\ \ \ f\ =}{\mathrm{g}}_{\mathrm{3}}{\mathrm{h}}_{\mathrm{3}}\mathrm{\ \ \ }\mathrm{\Rightarrow }\mathrm{\ \ \ }\mathrm{8}\mathrm{\ =\ }\frac{\mathrm{5}}{\mathrm{3}}\mathrm{\times }\frac{\mathrm{4}\mathrm{z}}{\mathrm{y}}\mathrm{\ }\mathrm{\Rightarrow }\mathrm{y\ =\ }\frac{\mathrm{4}\mathrm{\ \times \ }\mathrm{5}\mathrm{\ \times \ }\mathrm{24}}{\mathrm{3}\mathrm{\ \times \ }\mathrm{8}}\mathrm{=}\mathrm{20}$
$\mathrm{x\ }\text{محاسبه}\mathrm{\ \ \ }\mathrm{\Rightarrow }\mathrm{\ \ \ f\ =}{\mathrm{g}}_{\mathrm{2}}{\mathrm{h}}_{\mathrm{2}}\mathrm{\ \ \ }\mathrm{\Rightarrow }\mathrm{\ \ \ }\mathrm{8}\mathrm{\ =\ }\frac{\mathrm{4}}{\mathrm{3}}\mathrm{\times }\frac{\mathrm{4}\mathrm{y}}{\mathrm{x}}\mathrm{\ }\mathrm{\Rightarrow }\mathrm{x\ =\ }\frac{\mathrm{4}\mathrm{\ \times \ }\mathrm{4}\mathrm{\ \times \ }\mathrm{20}}{\mathrm{3}\mathrm{\ \times \ }\mathrm{8}}\mathrm{=}\mathrm{33/13}$
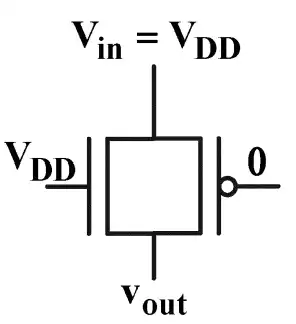
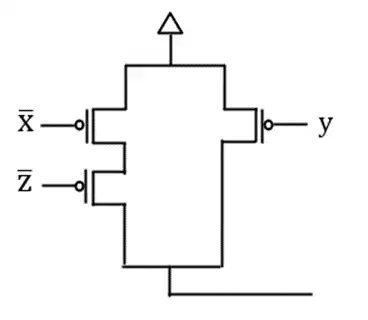
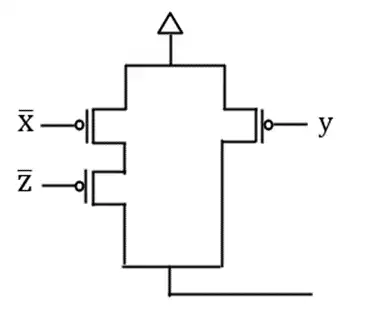
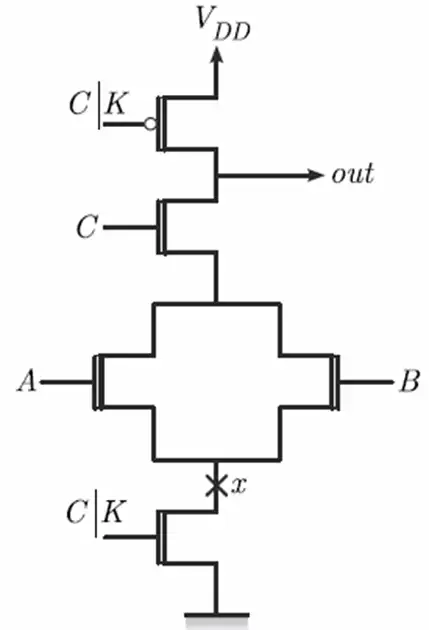
آسان کدام جمله در مورد خروجی یک گیت عبور به شکل زیر درست است؟ (فرض کنید $\left|V_{tn}\right|=\left|V_{tp}\right|$)
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
1ترانزیستور NMOS ولتاژ $V_{DD}-V_t$ روی خروجی قرار میدهد و ترانزیستور PMOS ولتاژ $V_{DD}$ روی خروجی میگذارد، لذا بین این دو ترانزیستور رقابت رخ میدهد و ولتاژ خروجی بین دو مقدار $V_{DD}$ و $V_{DD}-V_t$ خواهد بود.
2ترانزیستور NMOS پس از شارژ خروجی تا ولتاژ $V_{DD}-V_t$ خاموش میشود و ترانزیستور PMOS ولتاژ $V_{DD}$ روی خروجی قرار میدهد، لذا بدون رخ دادن هیچ رقابتی، خروجی برابر $V_{DD}$ خواهد شد.
3هر دو ترانزیستور ولتاژ $V_{DD}-V_t$ روی خروجی قرار میدهند، لذا خروجی برابر $V_{DD}-V_t$ خواهد شد.
4هر دو ترانزیستور ولتاژ $V_{DD}$ روی خروجی قرار میدهند، لذا خروجی برابر $V_{DD}$ خواهد شد.
در ابتدا $V_{out}$ برابر صفر است. در این حالت هر دو ترانزیستور N و P فعال بوده و از خود جریان به سمت Vout عبور میدهند، این فرآیند ادامه یافته تا اینکه Vout شارژ شده و به ولتاژ $V_{DD}-V_{t}$ میرسد.
از اینجا به بعد چون ولتاژ بین گیت و سورس ترانزستور نوع N (سمت چپی) از ولتاژ آستانه ($V_{t}$) کمتر (و برابر) میشود این ترانزیستور قطع میشود.
$V_{GS_n}=V_{DD}-V_{out}=V_{DD}-V_{DD}-V_t=V_t$
ولی با اینحال همچنان ترانزیستور نوع P فعال است و به عبور جریان ادامه میدهد، زیرا در این ترانزیستر ولتاژ میان گیت و سورس همیشه برابر $-V_{DD}$ بوده که از $-V_{t}$ کمتر است، بنابراین هیچوقت قطع نمیشود.
شرط روشن بودن PMOS:
$V_{GS}\ \lt \ -V_{t}$
حال با توجه به فرمول زیر که مربوط به حالت خطی این ترانزیستور میباشد، جریاندهی تا زمانی ادامه مییابد که $V_{out}=V_{DD}$ شود.
$I_{DS_p}=K_p\left[V_{SD}\left(V_{SG}-V_t\right)-\frac{V^2_{SD}}{2}\right],\ V_{SD}=V_{DD}-V_{out}$
بنابراین گزینه صحیح گزینه ۲ میباشد.
آسان یک ترانزیستور NMOS تخلیهای با $V_{TH}=-1^{(V)}$ و $\mathrm{\leftthreetimes }\mathrm{=}\mathrm{0/01}\mathrm{\ }و\mathrm{\ }µ_{\mathrm{n}}{\mathrm{C}}_{\mathrm{ox}}\left(\frac{\mathrm{W}}{\mathrm{L}}\right)\mathrm{=}\mathrm{100}\left(\frac{\mu \mathrm{A}}{{\mathrm{V}}^{\mathrm{2}}}\right)$ داریم. اگر بدانیم که $V_{GS}=\circ$ و $V_{DS}=2^{(V)}$ است، این ترانزیستور در چه ناحیهای قرار دارد و جریان عبوری از درون آن بر حسب $A\mu$ کدام است؟ خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
1اشباع و 51
2اشباع و 50
3تریودی و 102
4تریودی و 100
گزینه 1 صحیح است.
همانطور که میدانید در NMOS از نوع تخلیهای $V_t$ منفی است، پس داریم:
${\mathrm{V}}_{\mathrm{GS}}\mathrm{=}\mathrm{\circ }\mathrm{\ }=\mathrm{\ }{\mathrm{V}}_{\mathrm{t}}\mathrm{=-}\mathrm{2}\mathrm{\ }\mathrm{\Rightarrow }$ ترانزیستور روشن است
${\mathrm{V}}_{\mathrm{DS}}\mathrm{=}\mathrm{2}\mathrm{\ }=\mathrm{\ }{\mathrm{V}}_{\mathrm{GS}}\mathrm{-}{\mathrm{V}}_{\mathrm{t}}\mathrm{=}\mathrm{\circ }\mathrm{-}\left(\mathrm{-}\mathrm{1}\right)\mathrm{=}\mathrm{1}\mathrm{\ }\mathrm{\Rightarrow }$ در ناحیه اشباع است
با توجه به این که مقدار $\mathrm{\leftthreetimes }$ را ذکر شده است پس برای به دست آوردن جریان ${\mathrm{I}}_{\mathrm{DS}}$ داریم:
${\mathrm{I}}_{\mathrm{DS}}\mathrm{=}\frac{1}{2}\mu_{\mathrm{n}}{\mathrm{C}}_{\mathrm{ox}}{\left({\mathrm{V}}_{\mathrm{GS}}\mathrm{-}{\mathrm{V}}_{\mathrm{t}}\right)}^{\mathrm{2}}\left(\mathrm{1}\mathrm{\ +\ }{\mathrm{\leftthreetimes }\mathrm{V}}_{\mathrm{DS}}\right)\mathrm{=}\frac{1}{2}\times\mathrm{100}{\left(\mathrm{\circ }\mathrm{\ +}\mathrm{1}\right)}^{\mathrm{2}}\left( \mathrm{1}\mathrm{\ +\ }\mathrm{0/01}\mathrm{\ \times \ }\mathrm{2}\right)\mathrm{=}\mathrm{50}\mathrm{\ \times \ }\mathrm{1/02}\mathrm{\ =\ }\mathrm{51}\mathrm{\ }\mu \mathrm{A}$
آسان تابع و سطح ولتاژ خروجی گیت روبرو را تعیین کنید. (ترانزیستورها از نوع افزایشی (Enhancement) میباشند)
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
1$ f=\overline{\left(AB+D\right)\cdot C}\ \ \ \ \ \ \ \ 0\le v_{out}\le V_{DD} $
2$f=\left(A+B\right)\cdot D+C\ \ \ \ \ \ \ -V_{tp}\le v_{out}\le V_{DD}-V_{tn}\ $
3$ f=\left(\overline{A}\cdot \overline{B}+\overline{D}\right)\cdot \overline{C}\ \ \ \ \ \ \ \ V_{tn}\le v_{out}\le V_{DD}+V_{tp} $
4$ f=\left(\overline{A}+\overline{B}\right)\cdot \overline{D}+\overline{C}\ \ \ \ \ \ \ \ \left|V_{tp}\right|\le v_{out}\le V_{DD}-V_{tn} $
گزینه 2 صحیح است.
تعیین حدود ولتاژ:
ترانزیستورهای NMOS در زمان داشتن ولتاژ بالا در یکی از دو سر D, S برای اینکه روشن بمانند به اندازه $V_{tn}$ از ولتاژ آن سر کم کرده و به سر دیگر میدهند.
به طور برعکس در ترانزیستورهای PMOS در زمان داشتن ولتاژ پایین در یکی از دو سر D, S برای اینکه روشن بمانند به اندازه $-V_{tp}$ (چون $V_{tp}$ خود منفی است) به ولتاژ آن سر اضافه کرده و به سر دیگر میدهند.
در اینجا برای اینکه بیشترین ولتاژ را بیابیم باید مسیر با کمترین NMOS از خروجی به $V_{DD}$ را پیدا کنیم. ترانزیستور C در این راه قرار داد و با توجه به توضیح بالا حداکثر $V_{DD}-V_{tn}$ را به خروجی میدهد.
برای یافتن کمترین ولتاژ باید مسیر با کمترین PMOS از خروجی به زمین را بیابیم. در این مسیر دو ترانزیستور C, D قرار دارند بنابراین کمترین مقدار با توجه به توضیح بالا برابر $-2V_{tp}$ میشود.
$-2V_{tp}\le V_{out}\le V_{DD}-V_{tn}$
(گزینه صحیح در تعیین محدوده اشتباه کرده است.)
تعیین عبارت منطقی:
عبارت منطقی را میتوان با دیدن NMOSها و یا PMOSها مشخص کرد. در اینجا براساس NMOSها میرویم.
براساس NMOSها: (هر ترانزیستور اگر عبارت ورودیاش یک باشد روشن میشود.)
اگر ترانزیستور C روشن باشد خروجی ۱ میشود.
اگر ترانزیستور D روشن باشد و همراه آن یکی و یا هر دو از ترانزیستورها B, A روشن باشند خروجی ۱ میشود.
$\to C+\left(A+B\right)D$
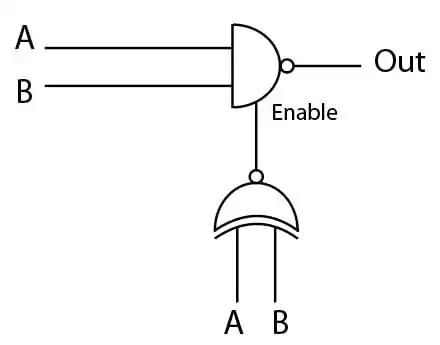
متوسط با حداقل چند ترانزیستور MOS میتوان عملکرد مدار زیر را پیادهسازی نمود؟ (دروازه NAND قابلیت حالت سوم دارد.)
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
1چهار عدد
2شش عدد
3بیش از چهارده عدد
4کمتر از چهارده و بیشتر از شش عدد
گزینه 1 صحیح است.
برای حل ابتدا خروجی را به ازای ورودیهای مختلف بدست میآوریم:
خروجی XNOR اگر صفر شود خروجی نهایی (Hight Impdance) HZ میشود، این اتفاق زمانی رخ میدهد که A, B یکی صفر و دیگری یک باشد.
در غیر این صورت XNOR یک بوده و NAND فعال است.
اگر A, B همزمان یک باشند خروجی NAND صفر و اگر همزمان صفر باشند خروجی یک میشود.
در نهایت داریم:
| $A$ |
$B$ |
$Out$ |
| $0$ |
$0$ |
$1$ |
| $0$ |
$1$ |
$HZ$ |
| $1$ |
$0$ |
$HZ$ |
| $1$ |
$1$ |
$0$ |
HZ به این معنی است که خروجی در آن زمان نه به صفر و نه به $V_{DD}$ متصل باشد.
CMOS جدول بالا به صورت زیر میشود:
آسان باتوجه به اطلاعات جدول روبرو، $V_{To}$ و $\mu_n$ را بیابید. $V_{SB}=0$
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
| $I_D(\mu A)$ |
$V_{DS}(V)$ |
$V_{GS}(V)$ |
| 685 |
5 |
5 |
| 365 |
4 |
4 |
| 145 |
3 |
3 |
| 106 |
0.3 |
5 |
| 52 |
0.2 |
4 |
| 16 |
0.1 |
3 |
1$V_{TO}=0.8V\ ,\ \mu_n=600\frac{cm^2}{v.s}$
2$V_{TO}=1.3V\ ,\ \mu_n=500\frac{cm^2}{v.s}$
3$V_{TO}=1V\ ,\ \mu_n=400\frac{cm^2}{v.s}$
4$V_{TO}=0.6V\ ,\ \mu_n=300\frac{cm^2}{v.s}$
گزینه 2 صحیح است.
فرمول جریان ترانزیستور NMOS به صورت زیر است:
در حالت خطی:
${\mu }_nC_{ox}\left(\frac{W}{L}\right)\left(V_{DS}\left(V_{GS}-V_{TO}\right)-\frac{V^2_{DS}}{2}\right)$
در حالت اشباع:
$\frac{1}{2}{\mu }_nC_{ox}\left(\frac{W}{L}\right){\left(V_{GA}-V_{TO}\right)}^2$
با توجه به این فرمولها ما تنها میتوانیم دو معادله متمایز تشکیل دهیم ولی همانطور که میبینید متغیرهای زیادی داریم. با اینحال میتوانیم ${\mu }_nC_{ox}(\frac{W}{L})$ را به عنوان یک متغیر $K_n$ در نظر گرفته و $V_{TD}$ را بیابیم. توجه کنید در این سؤال امکان یافتن $\mu_n$ به طور دقیق نیست.
سریعترین راه برای یافتن $V_{TD}$ انتخاب دو حالت اشباع و نوشتن فرمول جریان برای این دو حالت و سپس تقسیم دو طرف دو معادله بر یکدیگر است، چون در این حالت براحتی $K_n$ ها با هم خط میخورند و همین طور $V_{GS}$ که در فرمول جریان در حالت اشباع ترانزیستور بکار میرود در جدول داده شده است.
میدانیم که وقتی $V_{GS} \ ، \ V_{DS}$ با هم برابرند، ترانزیستور حتما در حالت اشباع است (اگر روشن باشد). برای همین ۲ ردیف اول را انتخاب میکنیم:
$\left\{ \begin{array}{c} \frac{1}{2}K_n{\left(5-V_{TO}\right)}^2=685 \\ \frac{1}{2}K_n{\left(4-V_{TO}\right)}^2=365 \end{array} \right.\to \frac{{\left(5-V_{TO}\right)}^2}{{\left(4-V_{TO}\right)}^2}=\frac{685}{365}$
$\to 365{\left(5-V_{TO}\right)}^2=685{\left(4-V_{TO}\right)}^2\to V_{TO}\approx \left\{\begin{array}{c} 4.5\ \ \text{غغق }\\ 1.3 \end{array} \right.$
(مقدار ۴.۵ به معنای خاموش بودن ترانزیستور است.)
متوسط تابع F با جدول درستی زیر را در نظر بگیرید. برای پیادهسازی این تابع با استفاده از مدار CMOS ایستا حداقل به چند ترانزیستور نیاز است؟ (فرض کنید فقط خود ورودیها در دسترس هستند.)
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
| F |
Z |
Y |
X |
| 1 |
0 |
0 |
0 |
| 1 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
| 1 |
1 |
0 |
1 |
| 0 |
0 |
1 |
1 |
| 1 |
1 |
1 |
1 |
112
210
38
46
گزینه 2 صحیح است. چون حداقل تعداد گیت خواستهشده، ابتدا جدول کارنو را رسم کرده و تابع خروجی را بدست میآوریم. سپس شکل مدار را رسم کرده و تعداد ترانزیستورهای به کار رفته را میشماریم:
$F\ =\ \bar{y}\ +\ xz$
حال با توجه به تابع بدست آمده، شبکه بالابر مدار CMOS گفته شده را رسم میکنیم:
از شکل بالا مشخص است که ما نیاز به 3 ترانزیستور PMOS در شبکه بالابر و 3 ترانزیستور NMOS در شبکه پایینبر داریم. همچنین چون دو متغیر در شکل بالا NOT شدهاند، نیاز به دو معکوس کننده CMOS که شامل 4 ترانزیستور هستند نیز داریم، که در مجموع به 10 ترانزیستور نیاز داریم.
دشوار معکوس کننده مقابل با فرض عدم صرفنظر از اثر بدن مقدار VOHکدام است؟
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
${\mathrm{(}V}_T\mathrm{=}\mathrm{0/7}\mathrm{(V)\ \ ,\ }\gamma \mathrm{=}{\mathrm{0/4}\mathrm{(}V\mathrm{)}}^{\frac{\mathrm{1}}{\mathrm{2}}}\mathrm{\ ,\ |}{\mathrm{\emptyset }}_F\mathrm{|=}\mathrm{0/32}\mathrm{)}$
14/3
24/07
33/92
43/78
گزینه 4 صحیح است.
برای این که VOHرا محاسبه کنیم، باید ورودی low باشد. در این حالت ترانزیستور pull - down خاموش است. ترانزیستور pull - up روشن است و باید روشن باقی بماند، پس:
$V_{OH}\mathrm{=}V_{DD}\mathrm{-}V_{T_L}\mathrm{\Rightarrow }V_{OH}\mathrm{=}V_{DD}\mathrm{-}\mathrm{(}V_{T_{L_{\mathrm{\circ }}}}\mathrm{+}\gamma \mathrm{(}\sqrt{\mathrm{2}\mathrm{|}{\mathrm{\emptyset }}_F\mathrm{|+}V_{SB}}\mathrm{-}\sqrt{\mathrm{2}\mathrm{|}{\mathrm{\emptyset }}_F\mathrm{|}}\mathrm{))}$
$\mathrm{\Rightarrow }V_{OH}\mathrm{=}\mathrm{5}\mathrm{-}\mathrm{(}\mathrm{0/7}\mathrm{+}\mathrm{0/4}\mathrm{(}\sqrt{\mathrm{0/64}\mathrm{+}V_{OH}}\mathrm{-}\sqrt{\mathrm{0/64}}\mathrm{))}$
$\mathrm{\Rightarrow }V_{OH}\mathrm{=}\mathrm{5}\mathrm{-}\mathrm{0/7}\mathrm{-}\mathrm{0/4}\sqrt{\mathrm{0/64}\mathrm{+}V_{OH}}\mathrm{+}\mathrm{0/32}\mathrm{\Rightarrow }{\mathrm{-}V}_{OH}\mathrm{+}\mathrm{4/62}\mathrm{=}\mathrm{0/4}\sqrt{\mathrm{0/64}\mathrm{+}V_{OH}}$
$\mathrm{\Rightarrow }\mathrm{0/16}\mathrm{(}\mathrm{0/64}\mathrm{+}V_{OH}\mathrm{)=}{\mathrm{(}\mathrm{4/62}\mathrm{+}V_{OH}\mathrm{)}}^{\mathrm{2}}\mathrm{\Rightarrow }\mathrm{0/1024}\mathrm{+}\mathrm{0/16}V_{OH}\mathrm{=}V^{\mathrm{2}}_{OH}\mathrm{-}\mathrm{9/24}V_{OH}\mathrm{+}\mathrm{21/3444}$
${\mathrm{\Rightarrow }V}^{\mathrm{2}}_{OH}\mathrm{-}\mathrm{9/4}V_{OH}\mathrm{+}\mathrm{21/242}\mathrm{=}\mathrm{\circ }\mathrm{\Rightarrow }V_{OH}\mathrm{=}\mathrm{5/62},\mathrm{3/78}$ غیر قابل
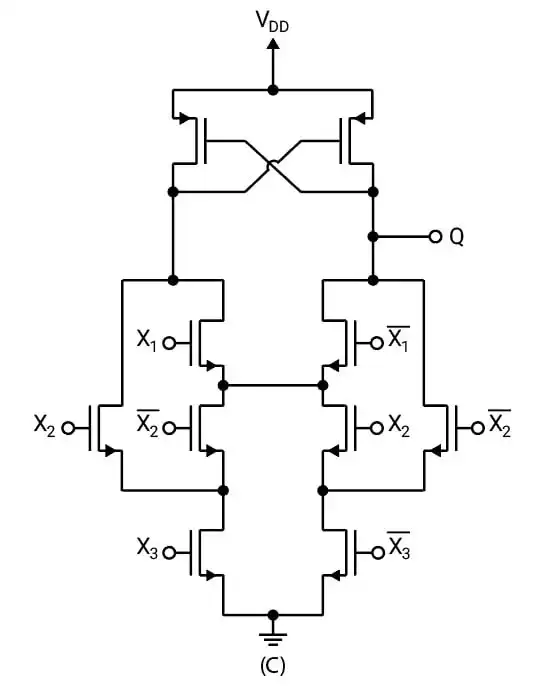
آسان خروجی Q برابر چه میباشد؟
خانواده ایستای MOSFETها، ترانزیستورهای اثر میدانی MOS، تحلیل مدارهای MOS
1$X_1X_2+X_1X_3+X_2X_3$
2$\overline{\overline{X_2}\overline{X_3}+\overline{X_1}X_2\overline{X_3}}$
3$X_1X_2X_3\left(X_1+X_2\right)\left(X_2+X_3\right)\left(X_1+X_3\right)$
4$\overline{\left(X_1+X_2\right)\left(X_2+X_3\right)\left(X_1+X_3\right)}$
گزینه 1 صحیح است.
در بالا Q یک PMOS وجود دارد که اگر سر گیت آن به زمین متصل شود Q برابر یک میشود. ابتدا بررسی میکنیم چه زمانی این گیت صفر میشود: (توجه کنید چون ترانزیستورهای پایین Q همگی NMOS میباشند در صورت یک بودن ورودی روشن میشوند.)
در صورت یک بودن $X_2X_3$: $X_2,X_3$
در صورت یک بودن $X_1,X_3$ و صفر بودن $X_1\overline{X_2}X_3$ :$X_2$
در صورت یک بودن $X_1,X_2$ و صفر بودن $X_1X_2\overline{X_3}$ :$X_3$
در نهایت داریم:
$Q=X_2X_3+X_1\overline{X_2}X_3+X_1X_2\overline{X_3} =X_2X_3+X_1\overline{X_2}X_3+X_2X_3+X_1X_2\overline{X_3} \\ =X_2\left(X_3+X_1\overline{X_3}\right)+X_3\left(X_2+X_1\overline{X_2}\right) \\ =X_2\left(\left(X_3+X_1\right)\left(X_3+\overline{X_3}\right)\right)+X_3\left(\left(X_2+X_1\right)\left(X_2+\overline{X_2}\right)\right) \\ =X_2X_3+X_2X_1+X_1X_3$
توجه کنید چون سمت راست مدار قرینه ورودیهای سمت چپ را دارد نیازی به بررسی صفرها نیست. همچنین در گزینهها، گزینهای مبنی بر وجود HZ یا خروجی غیرقابلقبول وجود ندارد.
آسان در شکل زیر خروجی out چه تابعی را پیاده سازی می کند؟
خانواده پویای MOSFETها
1$\overline{ABD\mathrm{'}E\mathrm{+}A\mathrm{'}C\mathrm{'}D\mathrm{'}E\mathrm{+}B\mathrm{'}C\mathrm{'}D\mathrm{'}E\mathrm{+}F}$
2$\overline{\mathrm{(}\overline{ABC}\mathrm{+}C\mathrm{')}D\mathrm{'}E\mathrm{+}F} $
3$\overline{\overline{\overline{\mathrm{(}ABC}\mathrm{+}C\mathrm{')}D\mathrm{'}}E\mathrm{+}F}$
4$\overline{ABCD\mathrm{'}E\mathrm{+}CD\mathrm{'}E\mathrm{+}F}$
گزینه 1 صحیح است.
این مدار در منطق NORA رسم شده است. در این منطق دو طبقه یکی در میان با Nmos و Pmos طراحی می شوند.
خروجی طبقه اول $\mathrm{=}\overline{ABC}$
خروجی طبقه دوم $\mathrm{=(}\overline{\overline{ABC}}\mathrm{+}C\mathrm{')}D\mathrm{'=(}ABC\mathrm{+}C\mathrm{')}D\mathrm{'}$
خروجی طبقه دوم $\mathrm{=[(}ABC\mathrm{+}C\mathrm{')}D\mathrm{'].}E\mathrm{+}F\mathrm{\ }\mathrm{\Rightarrow }\mathrm{\ }out\mathrm{=}\overline{\mathrm{(}ABC\mathrm{+}C\mathrm{')}D\mathrm{'}E\mathrm{+}F}\mathrm{\Rightarrow }$
اگر این عبارت را پخش کنید با گزینه 4 در یک not اختلاف دارد ولی با ساده سازی به صورت زیر می توانید به گزینه 1 برسید :
$ABC\mathrm{+}C\mathrm{'=}ABC\mathrm{+(}AB\mathrm{+}\overline{AB}\mathrm{)}C\mathrm{'=}ABC\mathrm{+}ABC\mathrm{'+}A\mathrm{'}C\mathrm{'+}B\mathrm{'}C' \\ \ \ \ \ \ \ \ \ \ \mathrm{=}AB\mathrm{+}A\mathrm{'}C\mathrm{'+}B\mathrm{'}C\mathrm{'}\mathrm{\Rightarrow }out\mathrm{=}\overline{\mathrm{(}AB\mathrm{+}A\mathrm{'}C\mathrm{'+}B\mathrm{'}C\mathrm{')}D\mathrm{'}E\mathrm{+}F} \\ \ \ \ \ \ \ \ \ \ \mathrm{=}\overline{ABD\mathrm{'}E\mathrm{+}A\mathrm{'}C\mathrm{'}D\mathrm{'}E\mathrm{+}B\mathrm{'}C\mathrm{'}D\mathrm{'}E\mathrm{+}F}$
دشوار در مدار شکل زیر گره x دچار مشکل چسبیده شدن به صفر شده است. اگر بدانیم که ورودی های مدار فقط در نیمه اول فاز pre charge اجازه تغییر دارند چه مقدار از ورودی ها این خطا را تشخیص می دهد؟
خانواده پویای MOSFETها
1$A+B=1 \ , \ C=1$
2$A+B=1 \ , \ C=0$
3$A=B=0 \ , \ C=1$
4قابل تشخیص نمی باشد.
گزینه 4 صحیح است.
اگر $A+B=1 , C=1$ نباشد که کلا چون شبکه پایین بر هیچ گاه وصل نیست پس مشکلی پیش نمی آید. اما اگر مثلا $A=C=1$ باشد آنگاه چه می شود. اگر $A=C=1$ باشد یعنی این مقدار از زمان نیمه pre charge تا آخر فاز ارزیابی باقی می ماند. در این صورت در نیمه فاز pre charge هردو شبکه بالابر و پایین بر وصل هستند و خروجی یک مقدار نامشخص می گردد ولی در فاز ارزیابی خروجی صفر میشود(چون شبکه بالابر قطع میشود) و مقدار صفر نیز درست است. ممکن است این سوال به ذهنتان برسد که فرض کنیم در نیمه اول $A=C=1$ ، pre charge باشد و بعد از آن مثلا $A=0$ شود در این صورت در نیمه اول pre charge خروجی مقداری نامشخص می گیرد ولی در نیمه بعدی خروجی 1 می شود و تا آخر ارزیابی نیز یک می ماند. توجه کنید که اگر فرض این که ورودی ها فقط در نیمه اول pre charge اجازه دارند تغییر کنند نبود آنگاه خطا با فرض این $C=A=1$ باشد و دقیقا قبل از فاز ارزیابی $A=0$ شود قابل تشخیص بود.
متوسط ساختارهای ترانزیستوری زیر سه پیادهسازی از یک NAND دو ورودی را در خانواده پویا (dynamic) نشان میدهند. ترتیب این گیتها از لحاظ سرعت بهترتیب از سریعترین به کندترین ساختار کدام است؟ (ترتیب در گزینهها از راست به چپ)
خانواده پویای MOSFETها
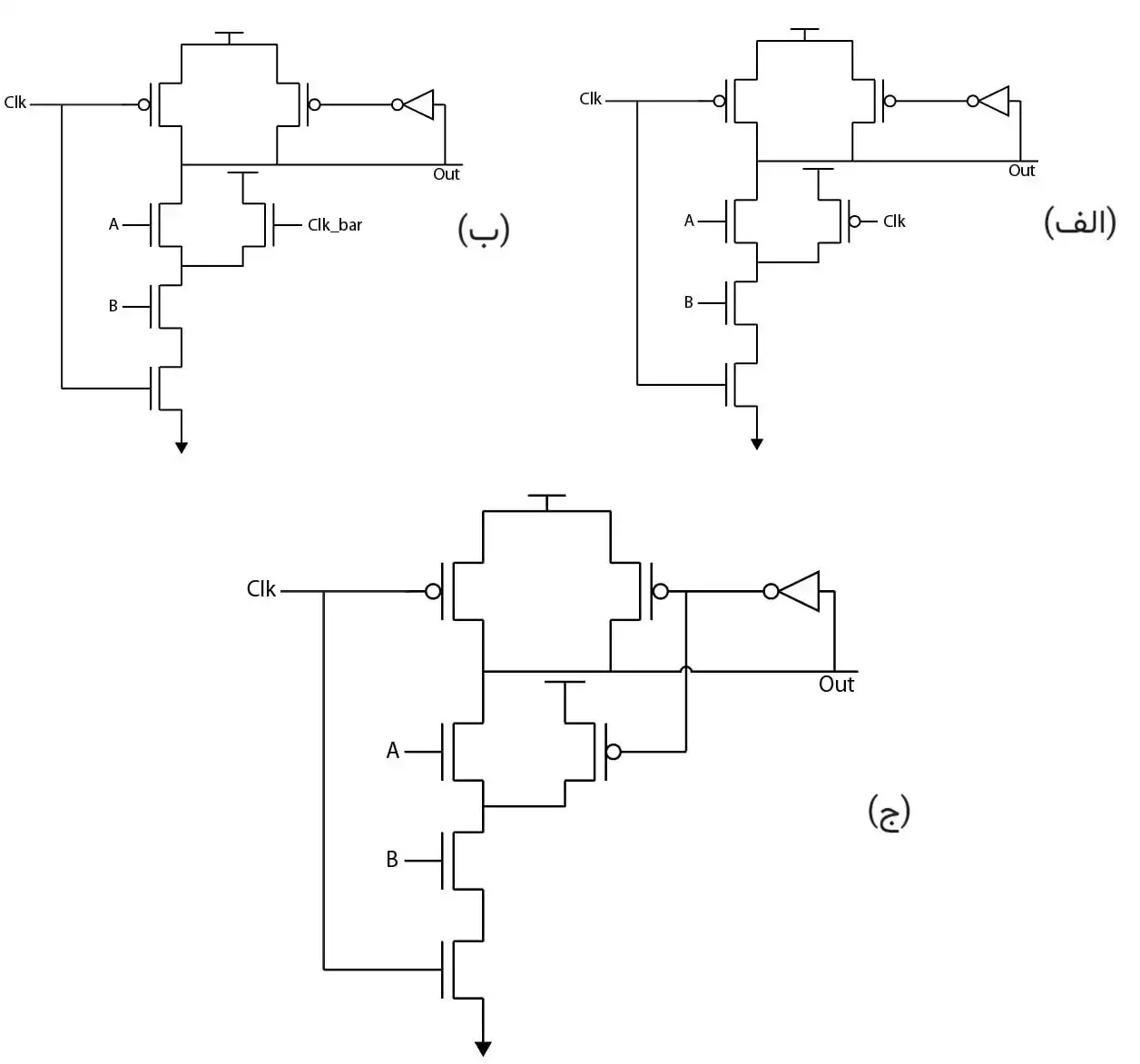
1(الف)(ب)(ج)
2(الف)(ج)(ب)
3(ب)(الف)(ج)
4(ج)(الف)(ب)
گزینه 3 صحیح است.
تفاوت مدارهای داده شده در ترانزیستور سمت راست ترانزیستورهای با ورودی A, B است. یک سر این ترانزیستور به $V_{dd}$ متصل است و سر گیت آن به CLK یا خروجی در زمان شارژ شدن متصل است. بنابراین این ترانزیستور در زمان شارژ شدن خروجی و زمانی که CLK=0 است روشن میشود و چون هدف آن شارژ کردن خروجی است هر چه زودتر روشن شود سرعت مدار بیشتر است.
در مدار الف و ب این ترانزیستور هماهنگ با CLK است و به محض اینکه CLK=0 میشود روشن میشود ولی در مدار ج باید ابتدا خروجی تا حدی شارژ شود تا این ترانزیستور روشن شود.
بنابراین سرعت الف و ب از ج بیشتر است.
حال سوال این است که الف سریعتر است یا ب؟
تفاوت الف و ب در استفاده از PMOS به جای NMOS است. NMOSها معمولا جریان دهی بیشتری از PMOSها دارند در اینجا نیز احتمالا طراح این نکته را در نظر گرفته و برای همین ب را سریعتر از الف قرار داده است.
(ب، الف، ج)
آسان در کدام جدول توان مصرفی مربوط به Switching Activity بیشتر است؟
توان مصرفی
الف)
| Out |
$B$ |
$A$ |
| $0$ |
$0$ |
$0$ |
| $0$ |
$1$ |
$0$ |
| $0$ |
$0$ |
$1$ |
| $1$ |
$1$ |
$1$ |
ب)
| Out |
$B$ |
$A$ |
| $1$ |
$0$ |
$0$ |
| $0$ |
$1$ |
$0$ |
| $1$ |
$0$ |
$1$ |
| $1$ |
$1$ |
$1$ |
ج)
| Out |
$B$ |
$A$ |
| $0$ |
$0$ |
$0$ |
| $1$ |
$1$ |
$0$ |
| $1$ |
$0$ |
$1$ |
| $0$ |
$1$ |
$1$ |
د)
| Out |
$B$ |
$A$ |
| $1$ |
$0$ |
$0$ |
| $1$ |
$1$ |
$0$ |
| $1$ |
$0$ |
$1$ |
| $0$ |
$1$ |
$1$ |
1الف
2ب
3ج
4ب و د
گزینه 3 صحیح است.
Switching activity زمانی بیشتر است که بیشتر تغییرات در خروجی نسبت به تغییر در ورودی داشته باشیم.
بررسی گزینهها:
الف) تغییرات خروجی در این گزینه زمانی رخ میدهد که از حالت دوم به چهارم و یا از حالت سوم به چهارم برویم (یا برعکس هر مسیر)
بنابراین در کل در این گزینه ۲ مسیر تغییر داریم.
ب) تغییرات خروجی در این گزینه زمانی رخ میدهد که از حالت اول به دوم و یا از حالت چهارم به دوم برویم (یا برعکس هر مسیر)
بنابراین در کل در این گزینه نیز ۲ مسیر تغییر داریم.
ج) تغییرات خروجی در این گزینه زمانی رخ میدهد که از حالت اول به دوم، دوم به چهارم، اول به سوم ویا سوم به چهارم برویم (یا برعکس هر مسیر)
بنابراین در کل در این گزینه ۴ مسیر تغییر داریم.
د) تغییرات خروجی در این گزینه زمانی رخ میدهد که از حالت دوم به چهارم و یا از حالت سوم به چهارم برویم (یا برعکس هر مسیر)
بنابراین در کل در این گزینه نیز ۲ مسیر تغییر داریم.
گزینه (ج) بیشترین تغییرات را دارد.
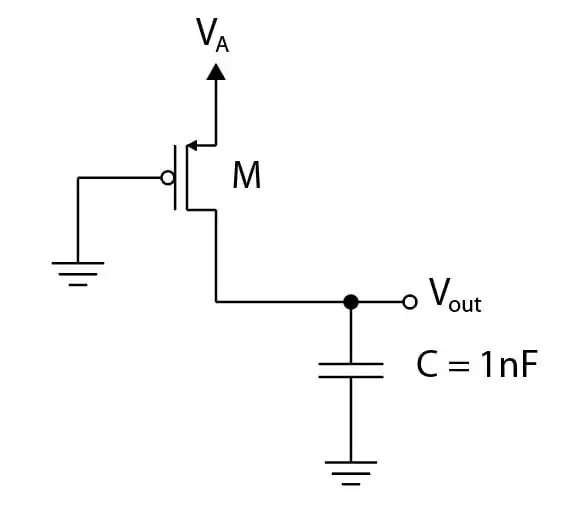
متوسط در مدار رو به رو، برای شارژ خازن ولتاژ $V_A$ را طی سه مرحله (هربار بعد از هر تغییر با فرصت کافی برای شارژ خازن) با پلههای دو ولتی مساوی از صفر به 6 ولت میرسانیم. انرژی کل تلف شده در ترانزیستور M را بیابید. ولتاژ آستانه ترانزیستور را
$-1V$ و از اثر بدنه صرفنظر کنید.
توان مصرفی
1ژول $6×10^{-9}$
2ژول $18×10^{-9}$
3ژول $36×10^{-9}$
4ترانزیستور PMOS بهعنوان کلید ایدهآل عمل میکند و تلفی ندارد.
گزینه 1 صحیح است.
مرحله اول شارژ شدن خازن از 0 تا 2 ولت را در نظر بگیرید. در این مرحله ترانزیستور (به عنوان به المان الکتریکی) ولتاژ دو سر آن با گذر جریان و شارژ شدن خازن از 2 تا 0 ولت کاهش مییابد و خازن ولتاژ آن از 0 تا 2 ولت افزایش مییابد.
در طول این افزایش و کاهش ولتاژ دو المان بارگذری از هر دو یکسان است. شاید در اینجا با تغییر وضعیت ترانزیستور شدت جریان تغییر کند ولی بارگذری در زمان کاهش ولتاژ از ۲ تا ۱ با بارگذری در زمان کاهش ولتاژ از ۱ تا ۰ یکسان است (جریان با شدت کم در زمان بیشتری عبور میکند.). انرژی مصرفی المانها از ضرب ولتاژ در جریان و انتگرال آنها در زمان بدست میآید. انرژی خازن در آن ذخیره میشود و انرژی مصرفی ترانزیستور تلف شده محسوب میشود. چون بارگذری یکسان است انرژی تلف شده و ذخیره شده یکسان میشوند.
انرژی نهایی خازن برابر است با:
$\frac{1}{2}CV^2=P_{Wasted}=\frac{1}{2}\times {10}^{-9}\times 2^2=2\times {10}^{-9}\ J$
در مراحل بعدی از دید ترانزیستور وضعیتی مشابه وضعیت مرحله اول داریم. در آنها نیز ولتاژ دو سر ترانزیستور 2 ولت کاهش مییابد و جریان گذری از آن هم مانند قبل میشود. بنابراین انرژی تلف شده مانند قبل است.
چون ۳ مرحله داشتیم انرژی تلف شده کلی برابر است با:
$3×2×10^{-9}=6×10^{-9} J$
آسان یک تراشۀ میکروپروسسور ساخته شده در تکنولوژی CMOS با ظرفیت یک میلیون دروازه منطقی، با منبع تغذیه 5 ولت کار میکند. کل مصرف توان با فرکانس پالس ساعت 120MHz معادل 9 وات و با پالس ساعت 50MHz معادل 4.7 وات میباشد. مصرف توان ایستا (Static) چقدر خواهد بود؟ توان مصرفی
1$P_{static} = 1.63W$
2$P_{static} = 4.3W$
3در تکنولوژی CMOS مصرف توان استاتیکی امکان ندارد.
4با این اطلاعات توان استاتیکی قابل محاسبه نیست.
گزینه 1 صحیح است.
توان کل مصرفی برابر با مجموع توان استاتیک و دینامیک میباشد. توان دینامیک رابطه مستقیمی با فرکانس کاری (یا همان فرکانس پالس در اینجا) دارد، به این معنی که با a برابر شدن این فرکانس توان دینامیک نیز a برابر میشود.
در اینجا فرکانس از 120MHz به 50MHz میرسد، در نتیجه توان دینامیک $\frac{50}{120}=\frac{5}{12}$ میشود.
$\left\{ \begin{array}{c} P_{static}+P_{dynamic}=9 \\ P_{static}+{\frac{5}{12}P}_{dynamic}=4.7 \end{array} \right.$
دستگاه بالا را حل میکنیم:
$\frac{7}{12}P_{dynamic}=4.3\to P_{dynamic}\approx 7.37W$
$\to P_{static}=9-7.37=1.63W$
متوسط طراحی یک مدار CMOS ایستا برای یک میکروکنترلر قرار است با فرکانس ۵۰۰ مگاهرتز کار کند. خروجی یک وارونگر نوعی در این طراحی با نرخ 0/1 فرکانس کلاک تغییر میکند و طبق مشخصات، مصرف توان نباید بیش از ۱۰ میکرووات باشد. بیشینه مقدار خازن بار وارونگر چند فمتوفاراد باشد تا این محدودیت برآورده شود؟ (VDD = 2V) از مصرف توان ایستا صرف نظر کنید.) توان مصرفی
110
250
3100
4500
.گزینه 2 صحیح است
$P_{Total}=P_{Dynamic}=\alpha CV_{DD}^2f_{CLK} \le 10\mu W\Rightarrow 0.1\times C\times 4\times500MHz\le 10\mu W$
$C\le 5\times 10^{-14}\Rightarrow C\le 50\times 10^{-15}\equiv50ff$
اشتراکhttps://www.konkurcomputer.ir/db71
 درس الکترونیک دیجیتال در تمامی دانشگاههای جهان به منظور آشنایی با مبانی الکترونیک و سختافزار و تکنولوژیهای استفاده شده از زمان پیدایش کامپیوتر تا کنون تدریس میشود مراجعه کنید.
درس الکترونیک دیجیتال در تمامی دانشگاههای جهان به منظور آشنایی با مبانی الکترونیک و سختافزار و تکنولوژیهای استفاده شده از زمان پیدایش کامپیوتر تا کنون تدریس میشود مراجعه کنید.