- لورم ایپسوم متن ساختگی با تولید سادگی نامفهوم دانلود
- لورم ایپسوم متن ساختگی با تولید سادگی نامفهوم دانلود
- لورم ایپسوم متن ساختگی با تولید سادگی نامفهوم دانلود
- لورم ایپسوم متن ساختگی با تولید سادگی نامفهوم دانلود
- لورم ایپسوم متن ساختگی با تولید سادگی نامفهوم دانلود
یک گیت AND میتواند دو یا چند ورودی و تنها یک خروجی داشته باشد. تصویر زیر نماد یک مدار AND و جدول بیانگر ترکیبات منطقی گیت است. (در تصویر نماد گیت، پایانه های ورودی در سمت چپ و پایانه خروجی در سمت راست قرار دارند). تنها زمانی خروجی گیت AND، یک خواهد شد که همه ورودی ها یک باشند.

| جدول درستی گیت AND | ||
|---|---|---|
| Q | B | A |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
صف (Queue)
هر ساختاری از دادهها که در آن عمل درج از یک طرف (انتها = Rear) و عمل حذف (سرویس) از طرف دیگر (ابتدا = Front) انجام شود، صف FIFO (First In First Out) نامیده شده که در بعضی مراجع به آن LILO (Last In Last Out) نیز گفته میشود.
پیادهسازی:
برای ذخیرهسازی ساختار یک صف میتوان یکی از 2 ساختار زیر را در نظر گرفت:
- آرایه (Array): که ساختاری ایستا (static) و محدود دارد.
- لیست پیوندی (Linked List): که ساختاری پویا (dynamic) و متناسب با دادهها دارد.
در صورتی که از آرایه n تایی $Q[1..n]$ برای نمایش و ذخیره ساختار یک صف استفاده شود همیشه از دو اشارهگر Front و Rear که به ترتیب به ابتدا و انتهای صف اشاره میکند استفاده میکنیم.
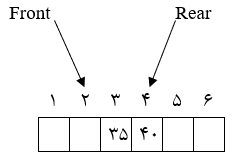
با توجه به شکل دیده میشود که:
Front: به خانه قبل از خانه اول صف اشاره میکند.
Rear: به خانه آخر صف اشاره میکند.
صف خطی
هر صف خطی یک آرایه n تایی $Q[1..n]$ که عناصر از ابتدای صف (Front) حذف شده و به انتهای صف (Rear) اضافه میشوند و حرکت عناصر برای درج به سمت جلو است در عین حال عمل حذف نیز خانههای خالی در ابتدای آرایه ایجاد میکند که با توجه به حرکت عناصر برای درج به سمت جلو امکان استفاده از این خانهها وجود ندارد.
مثال:
1) صف 6 عضوی روبهرو را در نظر بگیرید.
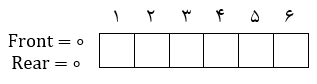
2) درج عناصر 10، 20، 35، 40
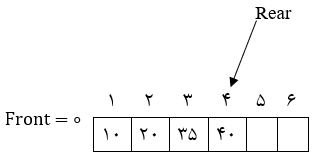
3) حذف 2 داده (بهطور عادی دادهها از ابتدا حذف میشوند).
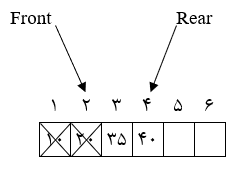
در وضعیت بالا با این که 2 داده از ابتدای صف حذف شدهاند اما فقط دو خانه 5 و 6 برای درج وجود دارند چون حرکت Rear به سمت جلو بوده و امکان استفاده از خانههای قبلی را ندارد.
شرایط مرزی و اولیه: (مهم)
$\text{ در صورتی که} $$\} $ $ \begin{array}{r} & \text{همیشه به خانه قبل از خانه اول صف اشاره کند.∶Front} \\ & \text{همیشه به خانه آخر صف اشاره کند.∶Rear} \\ \end{array} $
انتخاب آرایه $Q[1..n]$ برای پیادهسازی صف خطی دارای شرایط اولیه و مرزی زیر است:
| وضعیت اولیه صف | خالی بودن صف خطی | پر بودن صف خطی |
| Front = Rear = ∘ | Front = Rear | Rear = n |
عملیات در صف (Queue)
1- درج در صف
procedure insert (var item : data type);
begin
if rear = n then
write ('Queue is Full')
else
begin
rear := rear + 1;
Q[rear] := item;
end;
end;
دیده میشود که چون rear به خانه آخر صف اشاره میکند برای عمل درج ابتدا rear یک واحد به جلو حرکت کرده سپس داده item در خانه خالی انتهای صف درج میشود.
2- حذف از صف
procedure delete (var item : data type);
begin
if front = rear then
write ('Queue is Empty')
else
begin
front := front + 1;
item := Q[front];
end;
end;
دیده میشود که چون front همیشه به قبل از اول صف اشاره میکند برای عمل حذف ابتدا front 1 واحد به جلو حرکت کرده سپس داده ابتدای صف را خارج کرده در item قرار میدهد.
مشکل صفهای خطی
حرکت تدریجی عناصر به سمت انتهای صف و عدم امکان استفاده از خانههای ابتدای صف که در اثر حذف خالی شدهاند.
راهحل رفع مشکل صفهای خطی
شیفت خانههای انتهای صف به سمت ابتدای صف که این عمل در صورتی که تعداد خانههای صف زیاد باشد هزینه بالایی خواهد داشت.
استفاده از صف حلقوی به این مفهوم که زمانی که به انتهای صف رسیدیم عمل درج را دوباره از ابتدای صف انجام میدهیم و این حرکت چرخشی میباشد.
روش دوم در عمل مقرون به صرفهتر بوده و استفاده میشود.
صف حلقوی (Circular Queue)
آرایه n تایی $Q[∘ .. n-1]$ با ظرفیت n، همیشه یک خانه باید خالی باشد و حداکثر از $n-1$ خانه صف میتوان استفاده کرد. این به آن علت است که بتوان وضعیت پر یا خالی بودن صف حلقوی را تشخیص داد.میتوان به صورت یک صف حلقوی در نظر گرفت بهطوری که در این صف زمانی که rear برابر $n-1$ میشود، عنصر بعدی در خانه 0 قرار میگیرد.
| نمایش اول | 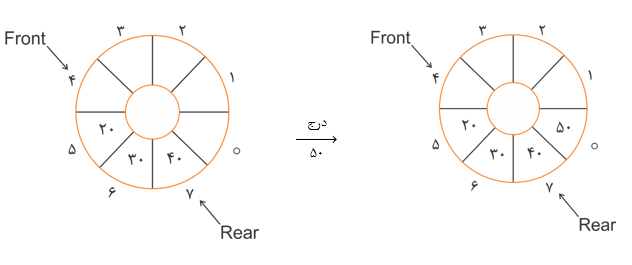 |
| نمایش دوم | 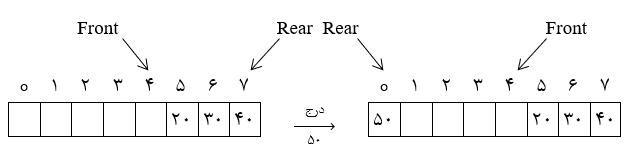 |
شرایط مرزی در صف حلقوی
| خالی (Empty) | پر (Full) |
| Front = Rear | Front = (Rear + 1) mod n |
تعداد خانههای قابل استفاده در صف حلقوی
در هر صف حلقوی $Q[∘ .. n-1]$ با ظرفیت n، همیشه یک خانه باید خالی باشد و حداکثر از $n-1$ خانه صف میتوان استفاده کرد. این به آن علت است که بتوان وضعیت پر یا خالی بودن صف حلقوی را تشخیص داد.
دقت کنید: در صورتی که در یک صف حلقوی $Q[∘ .. n-1]$ با ظرفیت n از همه خانههای صف استفاده کنیم و یک خانه را خالی نگذاریم وضعیت پر یا خالی بودن صف حلقوی قابل تشخیص نخواهد بود.
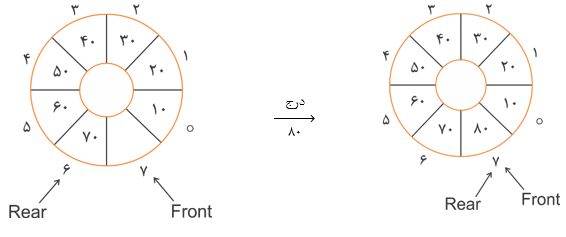
در مثال قبل بعد از درج 80 در صف حلقوی و استفاده از همان یک خانهای که باید در صف خالی میماند $Front = Rear = 7$ میشود که همان شرط خالی بودن صف است در صورتی که صف پر شده و این یک تناقض است برای نبودن تناقض فوق و امکان تشخیص وضعیت پر یا خالی بودن صف حلقوی یک خانه را خالی نگه میداریم.
عملیات در صف حلقوی
1- حذف از صف حلقوی
procedure delqueue (item : type);
begin
if front = rear then
write ('Queue is Empty')
else
begin
front := front + 1 mod n;
item := Q[front];
end;
end;
2- درج در صف حلقوی
procedure Addqueue (item : type);
begin
if (rear + 1) mod n = front then
write ('Queue is Full')
else
begin
rear := rear + 1 mod n;
Q[rear] := item ;
end;
end;
دقت کنید:
در هر دو روش حذف و درج به ترتیب از جملات $front ∶= (front + 1) mod \; n $ و $rear ∶= (rear + 1) mod \; n $ استفاده شده است که علت استفاده از mod در شرایطی است که front یا rear به خانه آخر اشاره کرده باشند و حرکت به جلو آنها را به ابتدای صف منتقل میکند.
تعداد خانههای پر و خالی یک صف حلقوی با ظرفیت n
الف) Front به قبل از اول صف اشاره میکند:
| ردیف | وضعیت | تعداد خانههای صف | تعداد خانههای خالی |
| 1 | $Rear \ge Front $ | $ Front - Rear $ | $ n-(Rear - Front) $ |
| 2 | $Rear \lt Front $ | $ n-(Front - Rear) $ | $Front - Rear$ |
تبصره: رابطه $ n-(Front - Rear) $ را میتوان به صورت $ n+(Rear-Front) $ نوشت.
مثال: برای یک صف حلقوی زیر با ظرفیت $n=8$ همواره داریم:
| خانههای صف : Rear - Front = 5 خانههای خالی : n- (Rear - Front) = 3 |
$Rear \ge Front $ | 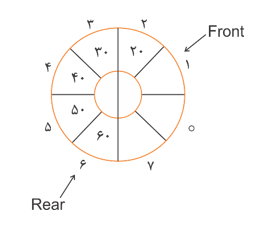 |
| خانههای صف : n - (Front - Rear) = 5 خانههای خالی : Front - Rear = 3 |
$Front \gt Rear $ | 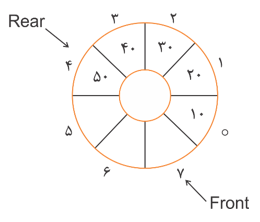 |
ب) Front به اول صف اشاره میکند:
| ردیف | وضعیت | تعداد خانههای صف | تعداد خانههای خالی |
| 1 | $Rear \ge Front $ | $ Rear - Front + 1$ | $ n-(Rear - Front + 1) $ |
| 2 | $Rear \lt Front $ | $ n-(Front - Rear - 1) $ | $Front - Rear -1$ |
بعضی از کاربردهای صف
- در صف پردازشهای سیستم عامل
- صف چاپگر
- پیمایش $BFS = Breath \;\;First\;\; Search$ (سطحی، ردیفی، پهنا) در درخت و گراف
لیستهای پیوندی (Linked List)
بهطور کلی برای ذخیرهسازی انواع دادهها در حافظه اصلی (RAM) از دو نوع ساختار میتوان استفاده کرد:
- آرایهها
- لیستهای پیوندی
آرایه
هر آرایه لیست پشت سرهمی از دادهها است که همگی دادهها از یک نوع بوده و ناحیهای پیوسته از حافظه را در اختیار دارند.
نکات مهم در آرایهها:
- تعداد عناصر هر آرایه همیشه محدود و مشخص و ایستا است و در تمام طول برنامه ثابت میباشد. (عیب)
-
عملیات حذف و درج یک داده دلخواه در خانهای از آرایه n عضوی نیاز به شیفت دارد. (عیب)
عملیات تعداد شیفت مورد نیاز متوسط شیفت مرتبه اجرایی درج داده در خانهی k ام $n-k+1$ $\frac{\mathrm{n\ +\ }\mathrm{1}}{\mathrm{2}}$ $o(n)$ حذف داده در خانهی k ام $n-k$ $\frac{\mathrm{n\ -\ }\mathrm{1}}{\mathrm{2}}$ $o(n)$ مثال:
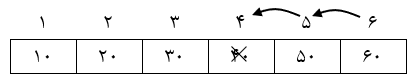
حذف 40 از محل $k=4$ ام از آرایه $n=6$ تایی نیاز به $n-k=6-4=2$ شیفت دارد.
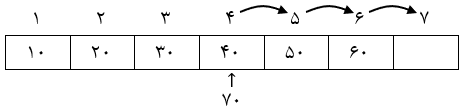
حذف 70 از محل $k=4$ ام از آرایه $n=6$ تایی نیاز به $n-k+1=6-4+1=3$ شیفت دارد.
دقت کنید: عملیات همراه با شیفت عناصر در شرایطی که n بزرگ باشد همواره هزینه بالایی دارد.
-
عملیات جستجو به دنبال یک دادهی دلخواه در آرایهها با یکی از دو روش زیر انجام میگیرد:
- جستجوی خطی (ترتیبی) در آرایههای مرتب یا نامرتب با زمان $o(n)$
- جستجوی دودویی (باینری) در آرایههای مرتب با زمان $o(log_2n)$ (مزیت)
مزیت در اینجا، امکان استفاده از جستجوی دودویی با زمان کمتر و سرعت بیشتر میباشد.
- دسترسی به دادههای هر آرایه به صورت تصادفی و دلخواه به راحتی توسط اندیس آرایه انجام شده و دسترسی مستقیم و با زمان $o(1)$ خواهد بود. (مزیت)
- روشهای مختلفی برای مرتبسازی آرایهها از قبیل: مرتبسازی حبابی- مرتبسازی انتخابی- مرتبسازی سریع- مرتبسازی درجی و... وجود دارد. (مزیت)
لیستهای پیوندی (Linked List)
لیست پیوندی، دارای عناصر (رکوردها) مختلفی از حافظه پویا (Heap) بوده که لزوماً عناصر آن کنار هم قرار نگرفتهاند.
لیست خانههای آزاد حافظه و اشارهگر (Avail)

آمادهسازی و ایجاد و تخصیص یک گره جدید
از آنجایی که هر گره (node) یک رکورد از فضای پویای (Heap) میباشد، برای ایجاد و تخصیص گرهای با اشارهگر دلخواه (مانند: p) از فضای آزاد و قابل دسترس (Available) با توجه به زبانهای مختلف برنامهسازی میتوان به صورت زیر عمل کرد:
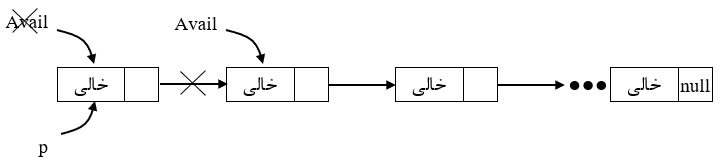
| زبان | الگوریتم |
| الگوریتمی | 1) if Avail = Null then write 'overflow' and exit 2) p = Avail , Avail = Link (Avail) |
| C | typedef struct node *List; typedef struct node { int Data; List Link;}; struct node *p; p = (struct node*) malloc (sizeof (struct node)) |
| PASCAL | Type List = ^ node; node = record Data : integer; Link : List; end; var p : ^node; new(p); |
نحوه دسترسی به فیلدهای هر گره
در صورتی که p اشارهگر به گرهای دلخواه باشد، برای دسترسی به فیلدهای گره
| زبان پاسکال | زبان C | زبان الگوریتمی |
| P^. Data | P → Data | Data[P] |
| P^. Link | P → Link | Link[P] |
در بعضی مراجع یا تستها بهجای Data از کلمه info استفاده میکنند.
مثال: در صورتی که گره با اشارهگر p به صورت nil or null or ∘ 20 باشد برای دسترسی به گرهها خواهیم داشت:
| زبان الگوریتمی | زبان پاسکال | زبان C |
| Data[P] = 20; | P^. Data := 20; | P → Data = 20 |
| Link[P] = 0; | P^. Link := nill; | P → Link = null |
null ,nil ,∘ یک مفهوم را دارند.
انواع لیستهای پیوندی
لیستهای خطی
-
لیست پیوندی یک طرفه (خطی): در هر گره فقط یک فیلد اشارهگر وجود دارد که آن هم آدرس گره بعدی را دارد.

-
لیست پیوندی دو طرفه (خطی): در هر گره دو فیلد اشارهگر وجود دارد که یکی به گره بعدی و دیگری به گره قبلی اشاره میکند.
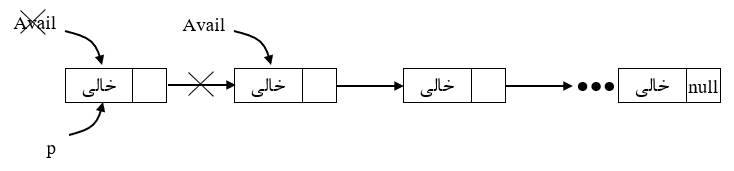
لیستهای دوری (حلقوی)
- در لیست حلقوی یک طرفه اشارهگر Link در گره آخر آدرس گره اول را داشته و به آن اشاره میکند.
- در لیست حلقوی دو طرفه اشارهگر سمت راست (Rlink) در گره آخر به گره اول و اشارهگر سمت چپ (Llink) در گره اول به گره آخر اشاره میکند.
1- لیست حلقوی یک طرفه
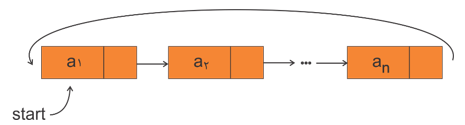
2- لیست حلقوی دو طرفه
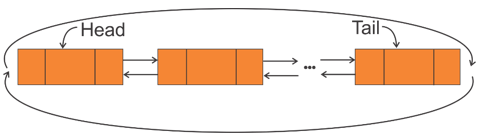
دقت کنید:
- بین لیستهای دوری و غیردوری تفاوتی از نظر اتلاف حافظه وجود ندارد، با این وجود اتلاف حافظه در لیستهای دو طرفه بیشتر از یک طرفه میباشد.
- یکی از مزایای مهم لیستهای دوری یک طرفه نسبت به لیستهای خطی یک طرفه این است که در لیستهای دوری یک طرفه امکان رسیدن به گره قبلی از هر گره دلخواه با چرخش از انتها به ابتدا در زمان $O(n)$ وجود دارد اما در لیستهای خطی یک طرفه این عمل امکانپذیر نیست.
با این وجود در لیستهای دو طرفه رسیدن از هر گره به گره ماقبل سریعتر و آسانتر از لیستهای دوری انجام میشود. چون در هر گره یک اشارهگر Llink به گره قبل وجود دارد و مانند لیست حلقوی نیازی به رفتن به انتهای لیست و برگشت به ابتدای لیست نخواهد بود و در زمان $O(1)$ انجام میشود.
جستجو در لیست پیوندی
جستجو در هر لیست پیوندی فقط و فقط به صورت ترتیبی امکانپذیر بودن و از ابتدای لیست آغاز میشود. مرتبه اجرایی جستجوی کلید دلخواه k در لیست پیوندی با n گره که اشارهگر start به ابتدای آن اشاره میکند برابر $O(n)$ است.
search(start,k)
if start ≠ nil
p = start
while p ≠ nil and data[p] ≠ k
p = Link[p]
return p
درج گره در لیست پیوندی یک طرفه
برای درج یک گرهی جدید در موقعیتی مشخص از یک لیست پیوندی، باید ابتدا با پیمایش لیست به موقعیت قبل از محل درج رسیده و سپس گره مورد نظر را درج کرد.
میخواهیم گره جدید با اشارهگر New را بعد از گره معلوم با اشارهگر Loc از لیستی که اشارهگر Start به ابتدای آن اشاره میکند درج کنیم، عملیات لازم عبارتند از:
آمادهسازی گره جدید با اشارهگر New
| نمایش وضعیت | الگوریتم |
 |
if Avail = nil then 'overflow' and 'exit' New = Avail , Avail = Link [Avail] data [New] = item Link [New] = nil |
درج گره جدید با اشارهگر New
| نمایش وضعیت | الگوریتم |
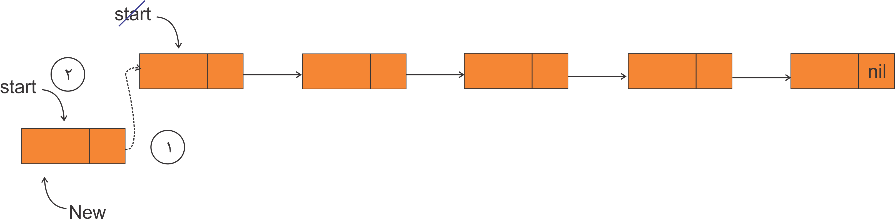 الف) زمانی که موقعیت قبل از درج (Loc = nil) باشد یعنی گره جدید باید در ابتدا درج شود. 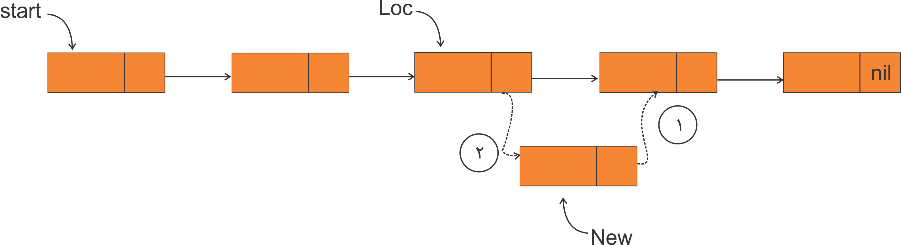 ب) زمانی که موقعیت قبل از درج (Loc ≠ nil) باشد یعنی گره جدید باید بعد از آن درج شود. |
if (Loc = nil) then 1) Link[New] = start ⇒ 2) start = New else 1) Link[New] = Link[Loc] ⇒ 2) Link[Loc] = New |
دقت کنید:
در صورتی که دستورات (2) و (1) جابهجا شود، ادامه لیست از موقعیت (Loc) به بعد گم میشود.
نتایج
- پیمایش لیستی با n گره برای رسیدن به موقعیت قبل از درج زمانی معادل $O(n)$ صرف میکند.
- برای درج هر گره جدید نیاز به 2 عمل جایگزینی است که زمانی معادل $O(1)$ صرف میکند.
الگوریتم بالا در زبانهای برنامهسازی مختلف میتواند به صورت زیر باشد:
| زبان C | زبان پاسکال |
|
if (Loc ═ null) then { New → link = start; start = New; } else { New → Link = Loc → Link; Loc → Link = New; } |
if Loc = nil then Begin New^. link := start; start := New; End else Begin New^. Link := Loc^. Link; Loc^. Link := New End |
حذف گره از یک لیست پیوندی (یک طرفه)
برای حذف گرهای دلخواه از موقعیتی مشخص از یک لیست پیوندی، باید ابتدا با پیمایش لیست به موقعیت قبل از محل حذف رسیده، سپس گره مورد نظر را حذف کرد.
میخواهیم گرهای دلخواه با اشارهگر x را که اشارهگر y به گره قبل از آن اشاره میکند حذف کنیم.
| نمایش وضعیت | الگوریتم |
 |
if (y = nil) then start = Link[start] ⇒ |
| الف) زمانی که موقعیت قبل از حذف (y = nil) باشد یعنی گره اول لیست باید حذف شود. | |
 |
else Link[y] = Link[x]⇒
|
| ب) زمانی که موقعیت قبل از حذف (y ≠ nil) باشد یعنی گره با اشارهگر (x) باید حذف شود. |
دقت کنید:
بهجای جملهی Link[y] = Link[x] میتوان از جملهی Link[y]=Link[Link[y]] استفاده کرد.
نتایج
- پیمایش لیستی با n گره برای رسیدن به موقعیت قبل از حذف زمانی معادل $O(n)$ صرف میکند.
- برای حذف هر گره نیاز به 1 عمل جایگزینی است.
- الگوریتم بالا در زبانهای برنامهسازی مختلف میتواند به صورت زیر باشد:
| زبان C | زبان پاسکال |
|
if (y ═ null) then start = start → link; else y → Link = x → Link; |
if y = nil then start := start^.link; else y^.Link := x^.Link; |
تبصره: در صورتی که بخواهیم گره حذف شده با اشارهگر x را آزاد کنیم (به ابتدای لیست در دسترس با اشارهگر Avail اضافه کنیم)، از دستورات 2 و 3 به شرح زیر استفاده میکنیم. این دستورات معادل توابع free, dispose در زبانهای پاسکال و C هستند.
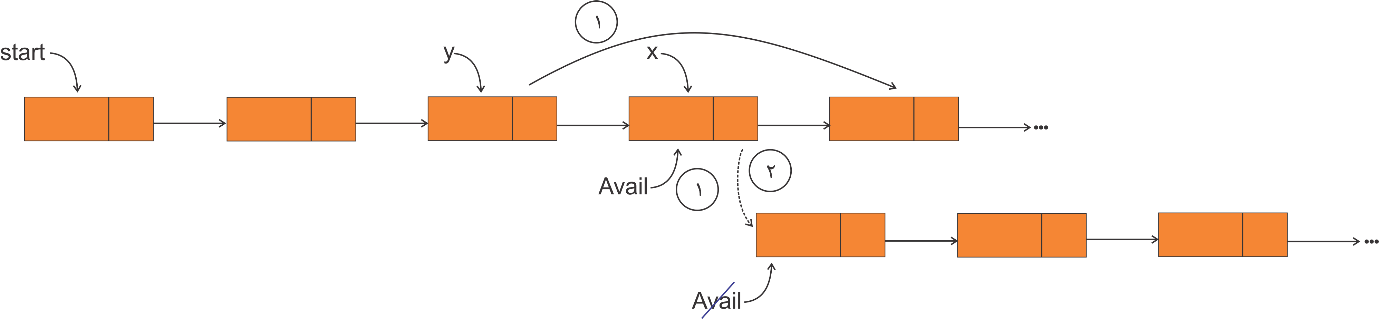
1) y^.link = x^.link
2) x^.link = Avail
3) Avail = x
مثال 1: یک لیست خطی یک طرفه با دو اشارهگر F و R که به ترتیب به عنصر اول و آخر لیست اشاره میکنند پیادهسازی شده است. هزینه کدامیک از اعمال زیر وابسته به تعداد عناصر لیست است؟ (کارشناسی ارشد- دولتی 80)

| 1) حذف اولین عنصر | 2) حذف آخرین عنصر |
| 3) درج یک عنصر در انتهای لیست | 4) درج یک عنصر در ابتدای لیست |
حل: گزینه 2 درست است.
برای درج و حذف گره از ابتدا (با استفاده از اشارهگر F) و درج گره در انتها (با استفاده از اشارهگر R) نیاز به پیمایش و وابسته به تعداد گرههای لیست نیست. اما برای حذف گره آخر ابتدا باید به کمک پیمایش در زمان O(n) به گره ماقبل آخر رسیده تا بتوان عمل حذف را انجام داد.
مثال 2: کدامیک از عبارتهای زیر نادرست است؟ (ارشد 84- IT)
1) $O(n!)=O(n^n)$
2) $O(10^6) \lt O(n) \lt O(n.log_2n)$
3) هر الگوریتم از مرتبه $θ(n)$، از مرتبه $O(n^2)$ نیز هست.
حذف عنصر آخر در یک لیست زنجیرهای یک طرفه، با داشتن اشارهگرهای first و last از مرتبه $O(1)$ است.
حل: گزینه 4 درست است.
برای حذف گره آخر ابتدا باید به کمک پیمایش در زمان $O(n)$ به گره ماقبل آخر رسیده تا بتوان عمل حذف را انجام داد.
پیمایش لیستهای پیوندی خطی
پیمایش گرههای یک لیست پیوندی خطی یک طرفه از ابتدای لیست انجام شده و به دو صورت بازگشتی و غیربازگشتی میتواند انجام گیرد.
الگوریتم غیربازگشتی
if start ≠ nil then
{
p := start
while(p ≠ nil)
{
Visit (Data[p]);
p = Link[p]
}
}
دقت کنید:
- شرط start ≠ nil در ابتدا تهی نبودن لیست پیوندی را کنترل میکند.
- در شرط حلقه while اگر از شرط Link[p] ≠ nil استفاده کنیم پیمایش لیست تا قبل از گره آخر انجام شده و با رسیدن اشارهگر p به گره آخر از حلقه خارج میشویم.
- پیمایش لیست پیوندی با n گره از مرتبه اجرایی O(n) است.
الگوریتم بازگشتی
الف) پیمایش از ابتدا تا انتها
Show (L : List)
{
if (L ≠ nil)
{
Visit (Data[L]);
Show (Link[L]);
}
}
ب) پیمایش از انتها تا ابتدا
Show (L : List)
{
if (L ≠ nil)
{
Show (Link[L]);
Visit (Data[L]);
}
}
در شرط دستور if اگر از شرط Link[L] ≠ nil استفاده کنیم پیمایش لیست تا قبل از گره آخر انجام شده و با رسیدن اشارهگر L به گره آخر از تابع بازگشتی خارج میشویم.
مثال: تابع زیر چه عملی انجام میدهد؟ توضیح این که list نشاندهنده لیستی از اعداد بوده و منظور از تابع Head، تابعی است که مقدار اولین عنصر در لیست را برمیگرداند و تابع tail لیستی حاوی همه عناصر لیست ورودی به استثنای اولین عنصر را برمیگرداند. مکانهای لیست را از مکان 1 در نظر بگیرید: (کارشناسی ارشد- دولتی 76)
function what (L : List) : integer;
begin
if L = nil then
what := (∘)
else
if Tail(L) ≠ nil then
what∶= (Head(L)+what(Tail(Tail(L))))
else
what := Head(L
end;
1) تعداد عناصر لیست را برمیگرداند.
2) مجموع عناصر در مکانهای فرد لیست ورودی را برمیگرداند.
3) تعداد عناصر در مکانهای فرد لیست را برمیگرداند.
4) مجموع عناصر لیست ورودی را برمیگرداند.
حل: گزینه 2 درست است.
لیست پیوندی حلقوی (Circular Linked List)
یک لیست پیوندی خطی یک طرفه که اشارهگر Link در گره آخر بهجای مقدار null آدرس گره اول لیست را نگهداری کرده و به آن اشاره میکند.
مزیت لیست حلقوی بر لیست خطی
مزیت لیست حلقوی (دوری) بر لیست خطی یک طرفه این است که در لیست حلقوی بدون نیاز به هیچ حافظه اضافی با داشتن آدرس یک گره دلخواه امکان دسترسی به گره قبلی وجود دارد (با پیمایش 1- n گره در لیست با n گره از مرتبه O(n)) ولی در لیست خطی یک طرفه این امکان وجود نداشته و دسترسی به گرههای قبل از یک گره فقط از طریق آدرس شروع لیست وجود دارد.
پیمایش لیست حلقوی
پیمایش یک لیست حلقوی در صورتی که start اشارهگری به ابتدای لیست حلقوی باشد به شرح زیر خواهد بود:
if start ≠ nil then
{
p = start;
repeat
Visit (Data[p]);
p = Link[p];
until p = start;
}
عملیات در لیستهای حلقوی
عملیات در لیستهای حلقوی مانند عملیات در لیستهای خطی است با این تفاوت که باید شرط پایان حلقهها و نحوه اصلاح اشارهگر گره آخر با توجه به دوری بودن لیست تغییر یابد.
مثال: فرض کنید a اشارهگر به انتهای یک لیست حلقوی و یک لیست غیرحلقوی باشد و بخواهیم گره x را بعد از آن درج کنیم.
| لیست دوری | $\gets$در صورتی که لیست تهی باشد$\rightarrow$ | لیست خطی |
| if (a≠nil) then
{ Link[x] = Link[a]; Link[a] = x; } else { a = x; Link[x] = x; } |
if (a≠nil) then { Link[x] = Link[a]; Link[a] = x; } else { a = x; Link[x] = nil; } |
دیده میشود برای درج در حالتی که لیست تهی نیست دو الگوریتم شبیه هم عمل میکنند اما زمانی که لیست تهی باشد دو وضعیت متفاوت به صورت زیر بعد از درج گره به وجود میآید:

لیست دوری و اشارهگر Start
در صورتی که اشارهگر Start در لیستهای دوری به گره اول یا آخر اشاره کند وضعیتهای متفاوتی از نقطهنظر زمان انجام بعضی از عملیاتها به وجود میآید که به شرح زیر آنها را بررسی میکنیم.
الف) اشارهگر Start به ابتدای لیست اشاره کند:
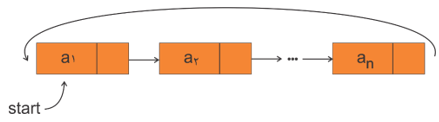
|
عملیات |
مرتبه اجرایی (زمان) |
توضیحات |
|
درج در ابتدا |
O(n) |
باید به انتهای لیست رفته تا گره جدید را در ابتدای لیست درج کنیم. |
|
حذف از ابتدا |
O(n) |
باید به انتهای لیست رفته تا گرهای را از ابتدای لیست حذف کنیم. |
|
درج در انتها |
O(n) |
باید به انتهای لیست رفته تا گره جدید را در انتهای لیست درج کنیم. |
|
حذف از انتها |
O(n) |
باید به گره ماقبل آخر رفته تا گره آخر را حذف کنیم. |
ب) اشارهگر Start به انتهای لیست اشاره کند:
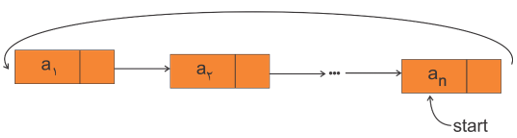
|
عملیات |
مرتبه اجرایی (زمان) |
توضیحات |
|
درج در ابتدا |
(1)O |
درج در انتها همان درج در ابتدا خواهد بود. |
|
حذف از ابتدا |
(1)O |
اشارهگر Start در انتها به راحتی گره را از ابتدا حذف میکند. |
|
درج در انتها |
(1)O |
درج در انتها به سادگی انجام خواهد شد. |
|
حذف از انتها |
O(n) |
باید به گره ماقبل آخر رفته تا گره آخر را حذف کنیم. |
اتصال (Concat) لیستهای پیوندی
اگر دو لیست پیوندی x و y به شرح زیر وجود داشته باشند، با استفاده از قطعه برنامه زیر میتوان این دو لیست را به هم متصل کرده و اشارهگر z را به ابتدای لیست حاصل از اتصال دو لیست x y , اشاره داد.
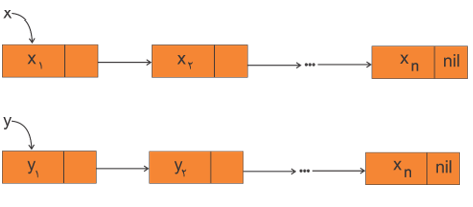
$if x = nil \ then z : = y$
$else$
$begin$
$ z : = x;$
$if y< \ >nil then$
$begin$
$\begin{cases} \\ {p\ ∶\ =\ x;\ }\\ \mathrm{while\ \ \ p^.\ link\ <\>\ nil\ \ \ do}\\ \mathrm{p\ ∶\ =\ p^.\ link;}\\ \mathrm{p^.\ link\ ∶\ =\ y;\ \ \ }\\ \mathrm{end;\ }\end{cases}$
$end;$
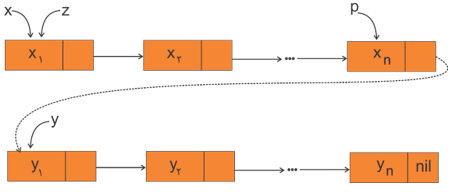
نکات 1- در شرط x = nil اگر x تهی باشد z به y اشاره خواهد کرد در غیر این صورت در قسمت else، z : = x شده و z به ابتدای لیست x اشاره خواهد کرد. 2- در قسمت else بعد از آن که z : = x انجام شد، با فرض آن که y تهی نباشد (در شرط $y<>nil$)، اشارهگر p در حلقه while، لیست x را پیمایش کرده تا روی گره آخر قرار گیرد، در این حالت از حلقه خارج شده و با جمله p^. link : = y، اشارهگر (link) گره آخر x به گره اول y اشاره کرده و الگوریتم پایان میپذیرد. 3- عملیات اتصال دو لیست x , y از مرتبه O(n) است. لیستهای پیوندی دو طرفه (Doubled Linked List) در لیستهای پیوندی دو طرفه هر گره به کمک دو اشارهگر Left (آدرس گره قبلی) و Right (آدرس گره بعدی) میتواند به گره قبلی و بعدی اشاره کند، در نتیجه با داشتن آدرس هر گره به راحتی میتوان به گره قبلی یا بعدی دسترسی پیدا کرد.
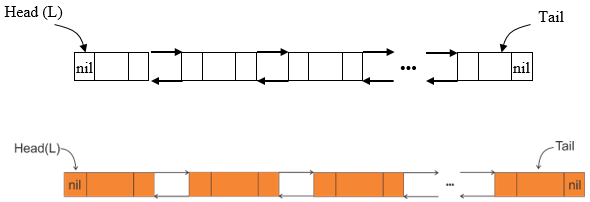
درج در لیستهای دو پیوندی
با داشتن آدرس یک گره دلخواه مانند P در یک لیست دو پیوندی میتوان گره جدید با اشارهگر New را در سمت چپ یا راست آن درج کرد. برای این کار به 4 عمل جایگزینی نیاز داریم.
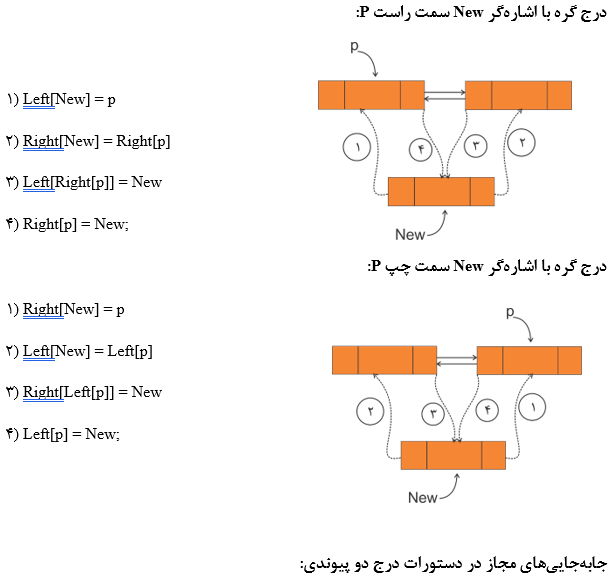
با کمی دقت میتوانیم ترتیبهای دستورات 1 تا 4 را به شرح زیر به 8 حالت جابهجا کنیم و گره با اشارهگر New به درستی درج شود.
|
3 |
3 |
3 |
1 |
2 |
2 |
2 |
1 |
|
2 |
2 |
1 |
3 |
3 |
3 |
1 |
2 |
|
4 |
1 |
2 |
2 |
4 |
1 |
3 |
3 |
|
1 |
4 |
4 |
4 |
1 |
4 |
4 |
4 |
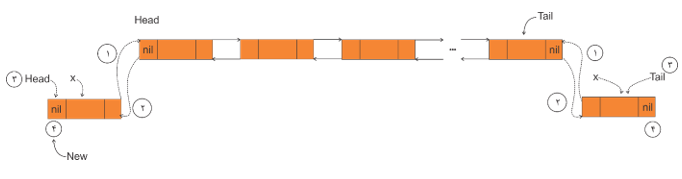
درج گره با اشارهگر x در ابتدا یا انتهای لیست:
|
1) left[x] = Tail 2) if Tail ≠nil then Right[Tail] = x 3) Tail = x4) Left[x] = nil; |
1) Right[x] = Head
2) if Head ≠nil then Left[Head] = x 3) Head = x4) Left[x] = nil; |
عمل حذف در لیستهای دو پیوندی
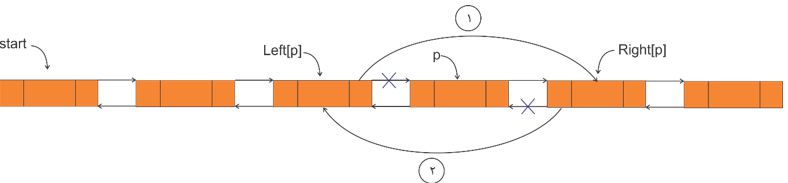
برای حذف گرهای دلخواه یک لیست دو پیوندی (دو طرفه) در صورتی که اشارهگر p به گره مورد نظر اشاره کند، با جایگزینی 2 آدرس به صورت زیر میتوان گرهی مورد نظر را حذف کرد:
1) Right [ Left[p]] = Right[p]
2) Left [Right[p]] = Left[p]
الگوریتم بالا در زبانهای برنامهسازی مختلف میتواند به صورت زیر باشد:
|
زبان C |
زبان پاسکال |
|
1) p → Left → Right = p → Right 2) p → Right → Left = p → Left |
1) p^. Left ^. Right = p^. Right 2) p^. Right ^.Left = p^. Left |
صف و پشته پیوندی
ساختارهای صف و پشته را میتوان با استفاده از لیستهای پیوندی پیادهسازی کرد. استفاده از لیستهای پیوندی در مقایسه با آرایهها برای پیادهسازی صف و پشته این مزیت را دارد که با استفاده از حافظه پویا و تخصیص این حافظه به صورت متناسب با دادهها از فضای حافظه بهطور بهینه استفاده میشود، این در حالی است که در آرایهها فضا به صورت محدود و ایستا در اختیار ساختارهای صف و پشته قرار میگیرد.
پشته پیوندی (Linked Stack)
هر لیستی که در آن عمل درج (push) و حذف (pop) عناصر از یک طرف (ابتدای لیست) انجام شود پشته پیوندی نامیده میشود.
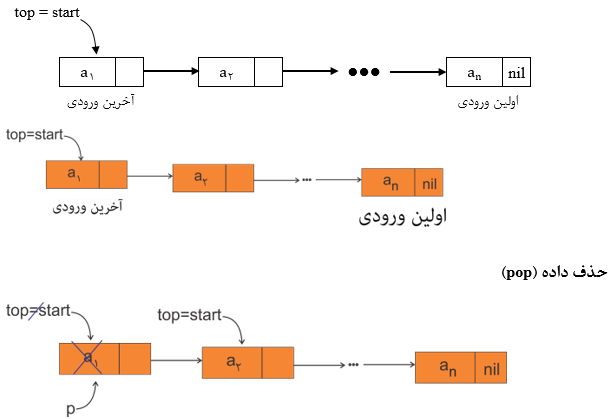
عمل حذف گره دلخواه در پشته پیوندی از ابتدای پشته (top = start) انجام میشود.
الگوریتم (pop):
1) p = start;
2) start = Link[start];
3) x = data[p];
4) free(p);
درج داده (push)
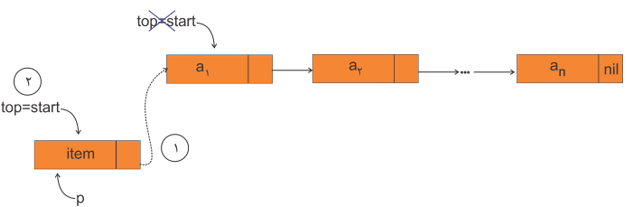
عمل درج گره دلخواه در پشته پیوندی در ابتدای پشته (top = start) انجام میشود.
الگوریتم (push):
الف) آمادهسازی گره با اشارهگر p برای درج:

ب) درج گره با اشارهگر p در ابتدای پشته (top = start):
1) p^. link = start
2) start = p
صف پیوندی (Linked Queue)
هر لیستی که عمل حذف از آن از یک طرف (ابتدای لیست) و عمل درج در آن در طرف دیگر لیست (انتهای لیست) انجام شود، صف پیوندی نامیده میشود.
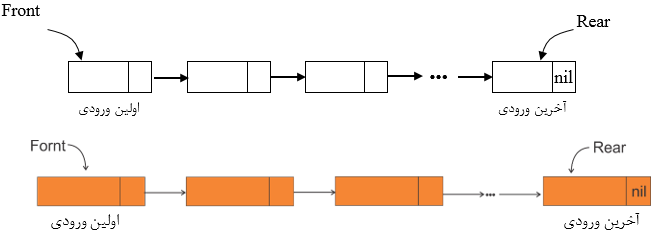
حذف از صف پیوندی
عمل حذف در صف پیوندی از ابتدا (front) انجام میشود.
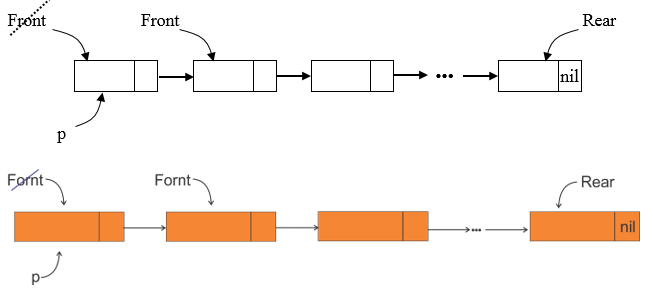 الگوریتم
الگوریتم
if (front = nil) then ʼQueue is emptyʼ
else
begin
1)p=front;
2)front=front^.link;
3)x=p^.data;
4)if (front=nil) then rear=nil
5)free(p);
end;
توضیحات:
1- در صورتی که شرط front = nil برقرار باشد صف خالی بوده و امکان حذف از آن وجود ندارد.
2- عمل حذف توسط دستور (2) انجام میشود.
3- در هر صف پیوندی بعد از هر عمل حذف ارزش گره حذفشده مورد ارزیابی قرار میگیرد به همین جهت دستورات (1) و (3) ارزش گره حذفشونده به کمک اشارهگر p در متغیر x نگهداری میکنند.
4- در صورتی که صف از ابتدا یک عضوی باشد (Front = Rear) بعد از عمل حذف توسط دستور (2) صف خالی شده و Front = nil شده و شرط دستور (4) برقرار بوده و باید Rear = nil شود.
5- آزادسازی گره حذفشده توسط دستور free (p) انجام میشود.
درج در صف پیوندی:
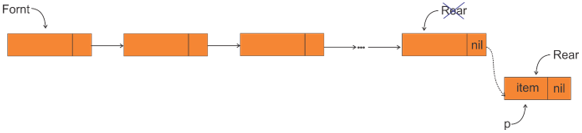
عمل درج گره دلخواه در صف پیوندی در انتها (Rear) انجام میشود.
مراحل درج:
الف) آمادهسازی گره با اشارهگر p برای درج
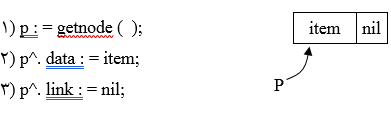
ب) درج گره با اشارهگر p در انتهای ساختار که دو حالت وجود خواهد داشت:
الگوریتم درج:
1) if Front = nil then
Front : = p;
else
2) Rear^. link : = p;
3) Rear : = p;
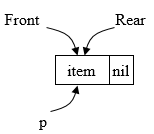
حالت اول:
صف تهی (Front = nil)
حالت دوم:
صفت غیرتهی
$(front \neq int)$
توضیحات:
1- در صورتی که دستور شرط (1) برقرار باشد، صف پیوندی تهی بوده (Front = nil) در نتیجه گره درجشونده با اشارهگر p تنها گرهی صف بوده و Front نیز باید به آن اشاره کند.
2- در صورتی که صف پیوندی تهی نباشد (قسمت else اجرا شده) و گره با اشارهگر p با دستور (2) به انتهای لیست درج میشود.
3- در هر وضعیتی (تهی یا غیرتهی)، اشارهگر Rear به کمک دستور (3) باید به گره با اشارهگر p به عنوان گره آخر اشاره کند.
معکوس کردن لیست پیوندی
الگوریتم غیربازگشتی
ابزار مورد نیاز:
برای معکوس کردن یک لیست پیوندی با هر تعداد گره تنها به 3 اشارهگر (p, q, r) نیاز داریم.
$p = start;$
$q = null;$
$while p \neq null do$
$begin$
$1) r = q;$
$2) q = p;$
$3) p = p^. link;$
$4) q. link = r;$
$end;$
$start = q;$
مرتبه اجرایی
زمان لازم برای معکوس کردن لیست پیوندی با n گره برابر با O(n) خواهد بود.
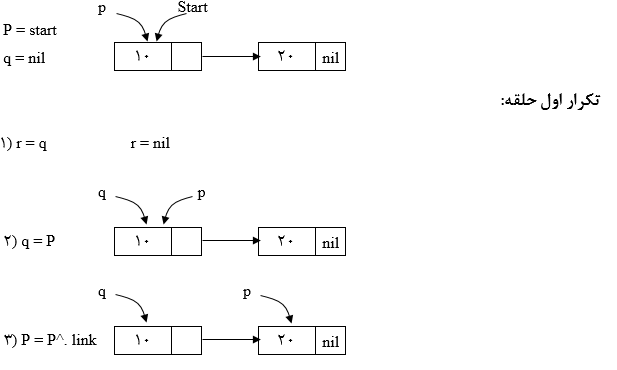
شروع الگوریتم:
p، به گره اول لیست اشاره میکند.
q، null میشود.
r، null میشود.
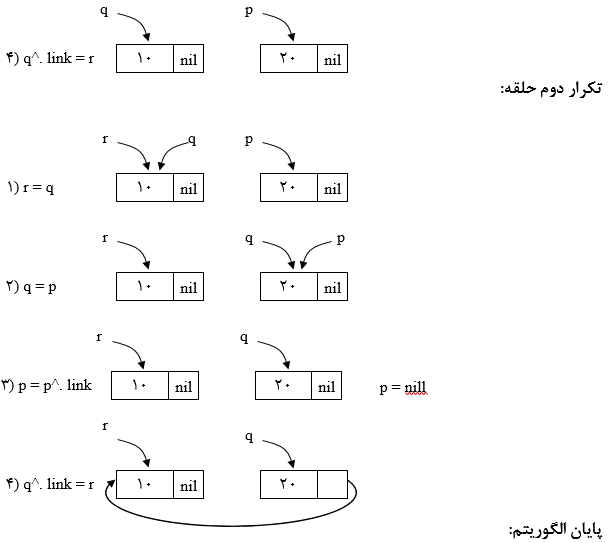
p، null میشود.
q، به ابتدای لیست معکوس شده اشاره میکند.
r، به یک گره بعد از q اشاره میکند.
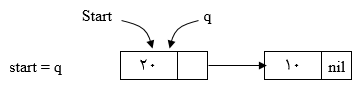
الگوریتم بازگشتی
reverse (s : list)
begin
if (s = nil) then return(nil)
else
$\mathrm{return}\left(\mathrm{cons}\left(\mathrm{reverse}\left(\mathrm{tail}\left(\mathrm{s}\right)\right)\ ,\ \mathrm{head} \left(\mathrm{s}\right)\right)\right)$
end;
cons (x , y): لیست y را به انتهای لیست x متصل میکند.
خصوصیات لیستهای پیوندی
مزایا:
1- تخصیص پویا و متناسب برای دادهها برخلاف آرایهها که تخصیص ایستا و محدود دارند.
2- عملیات درج و حذف بدون نیاز به شیفت با (1)O انجام میشود برخلاف آرایهها که نیاز به شیفت برای این عمل دارند با O(n).
معایب:
1- اتلاف حافظه نسبت به آرایهها به علت استفاده از فیلد اشارهگر بیشتر است.
2- تنها روش جستجو، جستجوی خطی است و با زمان O(n) برخلاف آرایهها که جستجو دودویی را نیز دارند با زمان$o(log_2n)$
- دسترسی به هر داده ترتیبی و از ابتدای لیست است با زمان O(n) برخلاف آرایهها که امکان دسترسی تصادفی با زمان (1)O را دارند.
نکته: با اجرای الگوریتم زیر بر روی لیست پیوندی، خروجی برابر است با: (L به ابتدای لیست پیوندی اشاره میکند.)

که شکل غیربازگشتی الگوریتم به صورت زیر است:
int S(List *L){
while(L->next!=L){
L->next=L->next->next;
L=L->next; $2(n-2^{[log n])}+1$: خروجی
}
return->data;
}
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| A | 87 | 48 | 52 | 29 | 23 | 48 | 49 | 21 | 12 | 24 | 17 |
آرایه ها
مجموعهای از دادههای پشت سر هم حافظه که همگی از یک نوع بوده و از آدرس مشخصی شروع میشوند. محاسبه آدرس خانه \(\mathrm{A}\left[\mathrm{i,\ j,\ k}\right]\) در آرایه \(\mathrm{A}\left[{\mathrm{L}}_{\mathrm{1}}..{\mathrm{U}}_{\mathrm{1}},{\mathrm{L}}_{\mathrm{2}}..{\mathrm{U}}_{\mathrm{2}},{\mathrm{L}}_{\mathrm{3}}..{\mathrm{U}}_{\mathrm{3}}\right]\)
برای محاسبه آدرس خانهی \(\mathrm{A}\left[\mathrm{i,\ j,\ k}\right]\) با توجه به وضعیت (سطری یا ستونی) همواره میتوانیم به صورت زیر عمل کنیم:
\(α\) = آدرس شروع آرایه (در صورت عدم بیان آدرس شروع \(α=\ \mathrm{\circ }\) فرض میکنیم)
\(\beta \) = فضای نوع عناصر آرایه (در صورت عدم بیان فضای نوع عناصر آرایه \(\beta =\mathrm{1}\) فرض میکنیم)
\(\mathrm{A}\left[\overline{\mathrm{i,\ j,\ k}}\right]=\mathrm{α}\mathrm{+}\left[\left(\mathrm{i}\mathrm{-}{\mathrm{L}}_{\mathrm{1}}\right)\left({\mathrm{U}}_{\mathrm{2}}-{\mathrm{L}}_{\mathrm{2}}+\mathrm{1}\right)\left({\mathrm{U}}_{\mathrm{3}}-{\mathrm{L}}_{\mathrm{3}}+\mathrm{1}\right)+\left(\mathrm{j}\mathrm{-}{\mathrm{L}}_{\mathrm{2}}\right)\left({\mathrm{U}}_{\mathrm{3}}-{\mathrm{L}}_{\mathrm{3}}+\mathrm{1}\right)+\left(\mathrm{k}\mathrm{-}{\mathrm{L}}_{\mathrm{3}}\right)\right]\times \mathrm{\beta }\) (آدرس سطری)
\(\mathrm{A}\left[\overline{\mathrm{i,\ j,\ k}}\right]=\mathrm{α}\mathrm{+}\left[\left(\mathrm{k}\mathrm{-}{\mathrm{L}}_{\mathrm{3}}\right)\left({\mathrm{U}}_{\mathrm{2}}-{\mathrm{L}}_{\mathrm{2}}+\mathrm{1}\right)\left({\mathrm{U}}_{\mathrm{1}}-{\mathrm{L}}_{\mathrm{1}}+\mathrm{1}\right)+\left(\mathrm{j}\mathrm{-}{\mathrm{L}}_{\mathrm{2}}\right)\left({\mathrm{U}}_{\mathrm{1}}-{\mathrm{L}}_{\mathrm{1}}+\mathrm{1}\right)+\left(\mathrm{i}\mathrm{-}{\mathrm{L}}_{\mathrm{1}}\right)\right]\times \mathrm{\beta }\) (آدرس ستونی)
دقت کنید:
-
این روش برای حالت n بعدی نیز به راحتی قابل تعمیم است.
-
در صورت عدم بیان نوع آدرس (سطری یا ستونی) بهطور پیشفرض آدرس سطری در نظر گرفته میشود.
مثال 1: آرایه 3 بعدی \(\mathrm{A}\left[\mathrm{1}\mathrm{:}\mathrm{15}\mathrm{,\ }\mathrm{-}\mathrm{5}\mathrm{:}\mathrm{5}\mathrm{,\ }\mathrm{10}\mathrm{:}\mathrm{25}\right]\) برای ذخیره اعداد صحیح به طول 2 بایت به کار گرفته است. اگر آرایه به صورت سطری از آدرس 2000 به بعد ذخیره شده باشد آدرس عنصر \(\mathrm{A}\left[\mathrm{5}\mathrm{,\ }\mathrm{2}\mathrm{,\ }\mathrm{15}\right]\) چیست؟
| 1) 3868 | 2) 3370 | 3) 3420 | 4) 3642 |
حل: گزینه 4 درست است.
\[\mathrm{A:\ }\left[\mathrm{1}..\mathrm{15},\mathrm{-}\mathrm{5}..\mathrm{5}\mathrm{,\ }\mathrm{10}..\mathrm{25}\right]\ \ \ \ \ \mathrm{\beta }\mathrm{\ =\ }\mathrm{2}\mathrm{\ \ \ \ \ }\mathrm{α}\mathrm{\ =\ }\mathrm{2000}\]
$$ \require{enclose} A = [\overline{5,2,12}] =\overset{2000}{\enclose{horizontalstrike}{α}} + [(5-1)(5-(-5)+1)(25-10+1)+(2-(-5))(25-10+1)+(15-10)]\times \overset{2}{\enclose{horizontalstrike}{\beta}} =2000+1642=3642 $$
مثال 2: آرایه دو بعدی \(\mathrm{X}\left[-\mathrm{5}..\mathrm{5}\mathrm{,\ }\mathrm{3}..\mathrm{33}\right]\) در آدرس 400 به بعد حافظه قرار دارد و هر خانه آرایه احتیاج به 4 بایت دارد. آدرس عنصر \(\mathrm{X}\left[\mathrm{4},\mathrm{10}\right]\) به روش ستونی کدام است؟
| 1) 1444 | 2) 1544 | 3) 844 | 4) 744 |
حل: گزینه 4 درست است.
\[\mathrm{X}\left[-\mathrm{5}..\mathrm{5}\mathrm{,\ }\mathrm{3}..\mathrm{33}\right]\ \ \ \ \ \mathrm{\alpha }\mathrm{\ =\ }\mathrm{400}\mathrm{\ \ \ \ }\mathrm{\beta }\mathrm{\ =\ }\mathrm{4}\]
$$ \require{enclose} X[\overline{4,10}] = \overset{400}{\enclose{horizontalstrike}{α}} + [(10-3)(5-(-5)+1)+(4-(-5))] \times \overset{4}{\enclose{horizontalstrike}{\beta}} = 400+344 = 744 $$
گاهی اوقات یک آرایه چند بعدی را به صورت سطری یا ستونی در یک آرایه یک بعدی ذخیره میکنند، در این صورت آدرس خانه مشخص در آرایه چند بعدی به شکل سطری یا ستونی در آرایه یک بعدی مورد نظر میباشد.
مثال 3: آرایه 3 بعدی \(\mathrm{A}\left[\mathrm{1}\mathrm{\ ..\ m,\ }\mathrm{1}\mathrm{\ ..\ n,\ }\mathrm{1}\mathrm{\ ..\ p}\right]\) در یک آرایه یک بعدی \(\mathrm{B}\left[\mathrm{1}\mathrm{\ ..\ m\ \times \ n\ \times \ p}\right]\) به روش سطر به سطر ذخیره شده است. آدرس عنصر \(\mathrm{A}\left[\mathrm{i,\ j,\ k}\right]\) در B کدام است؟
| 1) \(\left(\mathrm{i}\mathrm{-}\mathrm{1}\right)\mathrm{np+}\left(\mathrm{j}\mathrm{-}\mathrm{1}\right)\mathrm{m+}\left(\mathrm{k}\mathrm{-}\mathrm{1}\right)\) | 2) \(\left(\mathrm{i}\mathrm{-}\mathrm{1}\right)\mathrm{np+}\left(\mathrm{j}\mathrm{-}\mathrm{1}\right)\mathrm{p+}\left(\mathrm{k}\mathrm{-}\mathrm{1}\right)\) |
| 3) \(\mathrm{mnp\ +\ np\ \times \ }\mathrm{1}\) | 4) \(\mathrm{inp}\mathrm{\ +\ }\mathrm{jp}\mathrm{\ }\mathrm{+\ k}\) |
حل: گزینه 2 درست است.
\[\mathrm{A}\left[\mathrm{1}\mathrm{\ ..\ m,\ }\mathrm{1}\mathrm{\ ..\ n,\ }\mathrm{1}\mathrm{\ ..\ p}\right]\]
$$ \require{enclose} A[\overline{i,j,k}] = \overset{0}{\enclose{horizontalstrike}{α}} + [(i-1)(n-1+1)(p-1+1)+(j-1)(p-1+1)+(k-1)] \times \overset{1}{\enclose{horizontalstrike}{\beta}} = (i-1)np+(j-1)p+(k-1) $$
مثال 4: آرایه سه بعدی \(\mathrm{M}\left[\mathrm{1}\mathrm{\ ..\ a,\ }\mathrm{1}\mathrm{\ ..\ b,\ }\mathrm{1}\mathrm{\ ..\ c}\right]\) در یک آرایه یک بعدی \(\mathrm{N}\left[\mathrm{1}\mathrm{\ ..\ a\ \times \ b\ \times \ c}\right]\) به روش ستونی ذخیره شده است. آدرس عنصر \(\mathrm{M}\left[\mathrm{i,\ j,\ k}\right]\) در آرایه N کدام است؟
| 1) \( { a \times b \times c + b \times c \times 1 } \) | 2) \( { a \times b \times c + b \times c \times 1 } \) |
| 3) \(\left(\mathrm{k}\mathrm{-}\mathrm{1}\right)\mathrm{ab\ +\ }\left(\mathrm{j}\mathrm{-}\mathrm{1}\right)\mathrm{a\ +\ }\left(\mathrm{i}\mathrm{-}\mathrm{1}\right)\) | 4) \(\left(\mathrm{i}\mathrm{-}\mathrm{1}\right)\mathrm{bc\ +\ }\left(\mathrm{j}\mathrm{-}\mathrm{1}\right)\mathrm{c\ +\ }\left(\mathrm{k}\mathrm{-}\mathrm{1}\right)\) |
حل: گزینه 3 درست است.
\[\mathrm{M}\left[\mathrm{1}\mathrm{\ ..\ a,\ }\mathrm{1}\mathrm{\ ..\ b,\ }\mathrm{1}\mathrm{\ ..\ c}\right]\]
$$ { \require{enclose} M[\overline{i,j,k}] = \overset{0}{\enclose{horizontalstrike}{α}} + [(k-1)(b-1+1)(a-1+1)+(j-1)(a-1+1)+(i-1)] \times \overset{1}{\enclose{horizontalstrike}{\beta}} = (k-1)ba + (j-1)a + (i-1) } $$
محاسبه شماره خانه $\mathrm{A}\left[\mathrm{i,\ j,\ k}\right]$ در آرایه $\mathrm{A}\left[{\mathrm{L}}_{\mathrm{1}}..{\mathrm{U}}_{\mathrm{1}},{\mathrm{L}}_{\mathrm{2}}..{\mathrm{U}}_{\mathrm{2}},{\mathrm{L}}_{\mathrm{3}}..{\mathrm{U}}_{\mathrm{3}}\right]$
برای این که محاسبه کنیم \(\mathrm{A}\left[\mathrm{i,\ j,\ k}\right]\) چندمین خانه سطری یا ستونی ماتریس \(\mathrm{A}\left[{\mathrm{L}}_{\mathrm{1}}..{\mathrm{U}}_{\mathrm{1}},{\mathrm{L}}_{\mathrm{2}}..{\mathrm{U}}_{\mathrm{2}},{\mathrm{L}}_{\mathrm{3}}..{\mathrm{U}}_{\mathrm{3}}\right]\) است کافیست در شرایطی که \(α=\ \mathrm{\circ }\) و \(\beta =\mathrm{1}\) در نظر گرفتهایم به آدرس \(\mathrm{A}\left[\mathrm{i,\ j,\ k}\right]\) یک واحد اضافه کنیم.
$$ \require{enclose} A = [\overline{i,j,k}] =\bigl(\overset{0}{\enclose{horizontalstrike}{α}} + [(i-L_1)(U_2-L_2+1)(U_3-L_3+1)+(j-L_2)(U_3-L_3+1)+(k-L_3)] \times \overset{1}{\enclose{horizontalstrike}{\beta}}\bigr) + 1= [(i-L_1)(U_2-L_2+1)(U_3-L_3+1) + (j-L_2)(U_3-L_3+1) + (k-L_3)] +1 $$
$$ \require{enclose} A = [\overline{i,j,k}] =\bigl(\overset{0}{\enclose{horizontalstrike}{α}} + [(k-L_3)(U_2-L_2+1)(U_1-L_1+1) + (j-L_2)(U_1-L_1+1) + (i-L_1)] \times \overset{1}{\enclose{horizontalstrike}{\beta}}\bigr) + 1= [(k-L_3)(U_2-L_2+1)(U_1-L_1+1) + (j-L_2)(U_1-L_1+1) + (i-L_1)] +1 $$
مثال: در آرایه \(\mathrm{A}\left[\mathrm{'a'\ ..\ 'e'\ ,\ }\mathrm{1}\mathrm{\ ..\ }\mathrm{4}\right]\) ، درایه \(\mathrm{A}\left[\mathrm{'b'\ ,\ }\mathrm{3}\right]\) چندمین خانه آرایه است؟
چون وضعیت سطری یا ستونی مشخص نشده است پیشفرض به صورت سطری عمل میکنیم در ضمن فاصله \(\mathrm{'a'\ ..\ 'e'\ }\) را به شکل 5 .. 1 در نظر میگیریم بنابراین وضعیت \( A[2,3] \) در \( A[1 .. 5, 1 .. 4] \) مد نظر است.
\[\mathrm{A}\left[\mathrm{2}\mathrm{\ ,\ }\mathrm{3}\right]=\left(\mathrm{\circ }+\left[\left(\mathrm{2}\mathrm{-}\mathrm{1}\right)\left(\mathrm{4}\mathrm{-}\mathrm{1}\mathrm{+}\mathrm{1}\right)+\left(\mathrm{3}\mathrm{-}\mathrm{1}\right)\right]\times \mathrm{1}\right)+\mathrm{1}\mathrm{\ =}\mathrm{\ 7}\]
| 'a', 4 | 'a', 3 | 'a', 2 | 'a', 1 |
| 'b', 4 | 'b', 3 | 'b', 2 | 'b', 1 |
| 'c', 4 | 'c', 3 | 'c', 2 | 'c', 1 |
| 'd', 4 | 'd', 3 | 'd', 2 | 'd', 1 |
| 'e', 4 | 'e', 3 | 'e', 2 | 'e', 1 |
ماتریسها
به هر آرایه دو بعدی \( m \times n \) یک ماتریس یا جدول با m سطر و n ستون گفته میشود که تعداد mn خانه در آن وجود دارد.
ماتریس مربع
به هر ماتریس \( n \times n \) با \( n^2 \) خانه ماتریس مربع گفته میشود.
در هر ماتریس مربع \( n \times n \) مانند A روابط زیر بری اندیس خانه \( A [i,j] \) وجود دارد:
$\left\{ \begin{array}{c} \mathrm{i\ +\ j\ \lt n\ +\ }\mathrm{1}\mathrm{ \ \ }\mathrm{\textrm{بالای قطر فرعی است}}\mathrm{\ \ A}\left[\mathrm{i\ ,\ j}\right]\ \\ \mathrm{i\ +\ j\ =\ n\ +\ }\mathrm{1}\mathrm{ \ \ }\mathrm{\textrm{روی قطر فرعی است}}\mathrm{\ \ A}\left[\mathrm{i\ ,\ j}\right]\ \ \\ \mathrm{i\ +\ j\ \gt n\ +\ }\mathrm{1}\mathrm{ \ \ }\mathrm{\textrm{پایین قطر فرعی است}}\mathrm{\ \ A}\left[\mathrm{i\ ,\ j}\right] \end{array} \right.$
$\left\{ \begin{array}{c} \mathrm{i\ \lt j \ \ }\mathrm{\textrm{بالای قطر اصلی است}}\mathrm{\ \ A}\left[\mathrm{i\ ,\ j}\right]\ \\ \mathrm{i\ =\ j \ \ }\mathrm{\textrm{روی قطر اصلی است}}\mathrm{\ \ A}\left[\mathrm{i\ ,\ j}\right]\ \ \\ \mathrm{i\ \gt j \ \ }\mathrm{\textrm{پایین قطر اصلی است}}\mathrm{\ \ A}\left[\mathrm{i\ ,\ j}\right] \end{array} \right.\mathrm{ \ \ }$
$ \textrm{قطر فرعی} \mathrm{\ (i\ +\ j\ =\ n\ +\ )} $
$\mathrm{\swarrow }$
$ \textrm{قطر اصلی} \mathrm{\ (i\ =\ j)} $
$\mathrm{\searrow }$
| A ( 1 , 3 ) | A ( 1 , 2 ) | A ( 1 , 1 ) | |
| A ( 2 , 3 ) | A ( 2 , 2 ) | A ( 2 , 1 ) | |
| A ( 3 , 3 ) | A ( 3 , 2 ) | A ( 3 , 1 ) | |
| \( 3 \times 3 \) |
ماتریس بالا مثلث و پایین مثلث
در هر ماتریس مربع \( n \times n \)
- الف) اگر عناصر زیر قطر اصلی "∘" باشد ماتریس بالا مثلثی است.
- ب) اگر عناصر بالای قطر اصلی "∘" باشد ماتریس پایین مثلثی است.
|
\[\left[ \begin{array}{ccccc} \mathrm{X} & \mathrm{X} & \mathrm{X} & \mathrm{\dots } & \mathrm{X} \\ \circ & \mathrm{X} & \mathrm{X} & \mathrm{\dots } & \mathrm{X} \\ \circ & \circ & \mathrm{X} & \mathrm{\dots } & \mathrm{X} \\ \mathrm{\vdots } & \mathrm{\vdots } & \mathrm{\vdots } & \mathrm{\dots } & \mathrm{\vdots } \\ \circ & \circ & \circ & \mathrm{\dots } & \mathrm{X} \end{array} \right]\] (ب) بالا مثلثی |
\[\left[ \begin{array}{ccccc} \mathrm{X} & \circ & \circ & \mathrm{\dots } & \circ \\ \mathrm{X} & \mathrm{X} & \circ & \mathrm{\dots } & \circ \\ \mathrm{X} & \mathrm{X} & \mathrm{X} & \mathrm{\dots } & \circ \\ \mathrm{\vdots } & \mathrm{\vdots } & \mathrm{\vdots } & \mathrm{\dots } & \mathrm{\vdots } \\ \mathrm{X} & \mathrm{X} & \mathrm{X} & \mathrm{\dots } & \mathrm{X} \end{array} \right]\] (الف) پایین |
| ماتریسهای بالا مثلثی و پایین مثلثی | |
در هر ماتریس بالا مثلث یا پایین مثلث:
| X | X | ... | X | X | |
| X | X | ... | X | 0 | |
| X | X | X | 0 | 0 | |
| X | X | 0 | 0 | 0 | |
| X | 0 | 0 | 0 | 0 | |
| \( n \times n \) |
$\begin{array}{c} \mathrm{n} \\ \mathrm{+\ n}\mathrm{-}\mathrm{1} \\ \begin{array}{c} \mathrm{+}\ \mathrm{n}\mathrm{-}\mathrm{2} \\ \mathrm{+}\ \ \ \ \vdots \ \ \ \ \\ \begin{array}{c} \underline{\ \ \ \ \ \ \ \ \ \mathrm{1}\mathrm{\ \ \ \ \ }} \\ \frac{\mathrm{n(n\ +\ }\mathrm{1}\mathrm{)}}{\mathrm{2}} \\ \end{array} \end{array} \end{array}$
(تعداد خانههای مخالف صفر)
تعداد کل خانهها = $n^2$
تعداد خانههای مخالف صفر = $\frac{\mathrm{n(n\ +\ }\mathrm{1}\mathrm{)}}{\mathrm{2}}$
تعداد خانههای صفر = $\frac{\mathrm{n(n\ -\ }\mathrm{1}\mathrm{)}}{\mathrm{2}}$
ماتریس L قطری
هر ماتریس \( n \times n \) که در آن L قطر آن که قطر اصلی نیز شامل آن است مخالف صفر باشد ماتریس L قطری میگویند.
-
ماتریس L قطری فقط برای Lهای فرد تعریف میشود.
ماتریس تعداد خانه مخالف صفر نمایش ماتریس 1 قطری = ماتریس قطری N 0 0 X 0 X 0 X 0 0 \( n \times n \) ماتریس 3 قطری 3n-2 0 X X X X X X X 0 \( n \times n \) .
.
..
.
..
.
.ماتریس L قطری \[\mathrm{nL}\mathrm{-}\frac{{\mathrm{L}}^{\mathrm{2}}-\mathrm{1}}{\mathrm{4}}\simeq \mathrm{nL}\]
مثال 1: میخواهیم یک صفحه شطرنجی \( n \times n \) را با موزاییکهایی به شکل روبهرو فرش کنیم. بدیهی است که موزاییکها را میتوانیم در جهات مختلف درون دهیم. برای کدامیک از nها این کار ممکن است؟ (کارشناسی ارشد- دولتی 75)
| 1) 5 | 2) 8 | 3) 6 | 4) 7 |
حل: گزینه 2 درست است.
با توجه به این که موزاییک مورد نظر 4 خانه دارد پس برای فرش کردن یک جدول \( n \times n \) باید به تعداد مضربی از 4 موزاییک استفاده کرد.
مثال 2: در یک آرایه (Array) دو بعدی \( 5 \times 5 \) مقادیر خانههای سطر اول همگی یک میباشد. اگر محتوای بقیه خانههای ستونهای 1 و 5 برابر با صفر بوده و داشته باشیم: (کارشناسی ارشد- آزاد 71 و آزاد 72)
| برای I از 2 تا 5 و J از 2 تا 4 | \(\mathrm{A}\left(\mathrm{I}\mathrm{\ ,\ J}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\left(\mathrm{I}\mathrm{-}\mathrm{1}\mathrm{\ ,\ J}\mathrm{-}\mathrm{1}\right)+\mathrm{A}\left(\mathrm{I}\mathrm{-}\mathrm{1}\mathrm{\ ,\ J+}\mathrm{1}\right)\right)\) |
محتوای خانههای سطر سوم این آرایه چه خواهد بود؟
| 1) \(\mathrm{\circ }\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{\circ }\) | 2) \(\mathrm{\circ }\mathrm{\ \ \ \ \ }\frac{\mathrm{1}}{\mathrm{2}}\ \ \ \ \ \frac{\mathrm{1}}{\mathrm{2}}\ \ \ \ \ \frac{\mathrm{1}}{\mathrm{4}}\ \ \ \ \ \mathrm{\circ }\) |
| 3) \(\mathrm{\circ }\mathrm{\ \ \ \ \ }\frac{\mathrm{1}}{\mathrm{2}}\ \ \ \ \ \mathrm{1}\ \ \ \ \ \frac{\mathrm{1}}{\mathrm{2}}\ \ \ \ \ \mathrm{\circ }\) | 4) \(\mathrm{\circ }\mathrm{\ \ \ \ \ }\frac{\mathrm{1}}{\mathrm{4}}\ \ \ \ \ \frac{\mathrm{1}}{\mathrm{2}}\ \ \ \ \ \mathrm{1}\ \ \ \ \ \mathrm{\circ }\) |
حل: گزینه 3 درست است.
با توجه به توضیحات مربوط به ماتریس مورد بررسی در سؤال، آرایه دو بعدی فوق به صورت زیر شبیهسازی میشود.
\[\mathrm{A\ \ \ }\mathrm{\ \ } \begin{array}{c} \mathrm{\ } \\ \mathrm{1} \\ \mathrm{2} \\ \mathrm{3} \\ \mathrm{4} \\ \mathrm{5} \end{array} \begin{array}{c} \begin{array}{cccccccc} \mathrm{\ } & \mathrm{1} & \mathrm{2} & \mathrm{3} & \mathrm{4} & \mathrm{5} & \ & \mathrm{\ \ \ } \end{array} \\ {\left[ \begin{array}{ccccc} 1 & 1 & 1 & 1 & 1 \\ \circ & 1 & 1 & 1 & \circ \\ \circ & {{\frac{1}{2}}} & 1 & {{\frac{1}{2}}} & \circ \\ \circ & \mathrm{\ } & \mathrm{\ } & \mathrm{\ } & \circ \\ \circ & \mathrm{\ } & \mathrm{\ } & \mathrm{\ } & \circ \end{array} \right]}_{\mathrm{5}\mathrm{\ \times \ }\mathrm{5}} \end{array} \]
شرایط گفته شده در صورت سؤال به این صورت است که به ازای I از 2 تا 5 و J از 2 تا 4:
\[\mathrm{A}\left(\mathrm{I\ ,\ J}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\left(\mathrm{I}\mathrm{-}\mathrm{1}\mathrm{\ ,\ J}\mathrm{-}\mathrm{1}\right)+\mathrm{A}\left(\mathrm{I}\mathrm{-}\mathrm{1}\mathrm{\ ,\ J\ +\ }\mathrm{1}\right)\right)\]
بنابراین محتوای خانههای دیگر ماتریس را با استفاده از این رابطه به دست میآوریم:
\[\mathrm{A}\left(\mathrm{2}\mathrm{\ ,\ }\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\left(\mathrm{2}\mathrm{-}\mathrm{1}\mathrm{\ ,\ }\mathrm{2}\mathrm{-}\mathrm{1}\right)+\mathrm{A}\left(\mathrm{2}\mathrm{-}\mathrm{1}\mathrm{\ ,\ }\mathrm{2}\mathrm{\ +\ }\mathrm{1}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\left(\mathrm{1}\mathrm{\ ,}\mathrm{1\ }\right)+\mathrm{A}\left(\mathrm{1}\mathrm{\ ,\ }\mathrm{3}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\mathrm{+}\mathrm{1}\right)=\mathrm{1}\] \[\mathrm{A}\left(\mathrm{2}\mathrm{\ ,\ }\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\left(\mathrm{1}\mathrm{\ ,\ }\mathrm{2}\right)+\mathrm{A}\left(\mathrm{1}\mathrm{\ ,\ }\mathrm{4}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\mathrm{\ +\ }\mathrm{1}\right)=\mathrm{1}\] \[\mathrm{A}\left(\mathrm{2}\mathrm{\ ,\ }\mathrm{4}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\left(\mathrm{1}\mathrm{\ ,\ }\mathrm{3}\right)+\mathrm{A}\left(\mathrm{1}\mathrm{\ ,\ }\mathrm{5}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\mathrm{\ +\ }\mathrm{1}\right)=\mathrm{1}\] \[\mathrm{A}\left(\mathrm{3}\mathrm{\ ,\ }\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\left(\mathrm{2}\mathrm{\ ,\ }\mathrm{1}\right)+\mathrm{A}\left(\mathrm{2}\mathrm{\ ,\ }\mathrm{3}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{\circ }\mathrm{\ +\ }\mathrm{1}\right)=\frac{1}{\mathrm{2}}\] \[\mathrm{A}\left(\mathrm{3}\mathrm{\ ,\ }\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\left(\mathrm{2}\mathrm{\ ,\ }\mathrm{2}\right)+\mathrm{A}\left(\mathrm{2}\mathrm{\ ,\ }\mathrm{4}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\mathrm{\ +\ }\mathrm{1}\right)=\mathrm{1}\] \[\mathrm{A}\left(\mathrm{3}\mathrm{\ ,\ }\mathrm{4}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\left(\mathrm{2}\mathrm{\ ,\ }\mathrm{3}\right)+\mathrm{A}\left(\mathrm{2}\mathrm{\ ,\ }\mathrm{5}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\mathrm{\ +\ }\mathrm{\circ }\right)=\frac{1}{\mathrm{2}}\]
برای سطرهای چهارم و پنجم هم به این ترتیب ادامه میدهیم.
اما با توجه به این که صورت سؤال از ما محتویات سطر سوم را میخواهد ما تا سطر سوم حساب کرده و آن را گزارش میکنیم.
| سطر سوم \(\mathrm{:\ }\mathrm{\circ }\mathrm{\ ,\ }\frac{\mathrm{1}}{\mathrm{2}}\mathrm{,\ }\mathrm{1}\mathrm{\ ,\ }\frac{\mathrm{1}}{\mathrm{2}}\mathrm{,\ }\mathrm{\circ }\) |
مثال 3: فرض کنید (i , j) و (K , L) دو عنصر در یک صفحه \( 8 \times 8 \)باشند (مانند صفحه شطرنج) کدامیک از گزینههای زیر همقطر بودن آنها را تعیین میکند؟ (تهدید دو مهره فیل)(کارشناسی ارشد- علوم کامپیوتر 79)
| 1) \(\mathrm{if\ (i\ =\ K)\ or\ (j\ =\ L)\ then}\) |
| 2) \(\mathrm{if\ (i}\mathrm{-}\mathrm{K\ =\ j}\mathrm{-}\mathrm{L)\ or\ (i}\mathrm{-}\mathrm{K\ =\ L}\mathrm{-}\mathrm{j)\ then}\) |
| 3) \(\mathrm{if\ (i}\mathrm{-}\mathrm{K\ =\ j}\mathrm{-}\mathrm{L)\ then}\) |
| 4) \(\mathrm{if\ (i}\mathrm{-}\mathrm{K\ =\ j}\mathrm{-}\mathrm{L)\ or\ (i}\mathrm{-}\mathrm{K\ =\ L\ +\ }\mathrm{8}\mathrm{-}\mathrm{j)\ then}\) |
حل: گزینه 2 درست است.
برای حل این سؤال با آوردن مثال برای یک ماتریس \( 8 \times 8 \) و در نظر گرفتن وضعیت مهرههای فیل جواب را به دست میآوریم:
\[\left(\mathrm{i\ ,\ j}\right)\mathrm{\ \ }\ \mathrm{\ \ \ }↔\mathrm{\ \ \ \ \ }\left(\mathrm{K\ ,\ L}\right)\] \[\left(\mathrm{1}\mathrm{\ ,\ }\mathrm{3}\right)\mathrm{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\left(\mathrm{3}\mathrm{\ ,\ }\mathrm{1}\right)\] \[\left(\mathrm{1}\mathrm{\ ,\ }\mathrm{3}\right)\mathrm{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\left(\mathrm{6}\mathrm{\ ,\ }\mathrm{8}\right)\]
ماتریس اسپارس (تُنک، پراکنده، خلوت، sparse)
بنابر تعریف به هر ماتریس \( m \times n \) که تعداد خانههای صفر و بیارزش (nonvalue) در آن بیشتر از تعداد خانههای مخالف صفر باشد، ماتریس اسپارس میگویند.
نکته: حاصلضرب، جمع و تفریق ماتریسهای sparse ممکن است sparse نباشد.
| اسپارس نیست | \[ \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} + \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \] | جمع |
| اسپارس نیست | \[ \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} - \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & -1 \\ 0 & 0 \end{bmatrix} \] | تفریق |
| اسپارس نیست | \[ \begin{bmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 0 & 0 & 0 \end{bmatrix} \] | ضرب |
روشهای نگهداری ماتریسهای اسپارس
- «آرایه دو بعدی و ذخیره مختصات خانههای مخالف صفر (روش عمومی)»
- «آرایه یک بعدی برای نگهداری مقادیر مخالف صفر به کمک فرمول (رابطه)» در ماتریسهای بالا مثلث، پایین مثلث، سه قطری و ...
1- «آرایه دو بعدی و ذخیره مختصات خانههای مخالف صفر (روش عمومی)»
در صورتی که ماتریس اسپارس \( m \times n \) با r خانه مخالف صفر وجود داشته باشد، برای ذخیرهی آن از یک آرایه دو بعدی با 1 + r سطر و 3 ستون به شرح زیر استفاده میشود:
\[\mathrm{sparse}\left[\mathrm{1}\mathrm{\ ..\ r+}\mathrm{1}\mathrm{\ ,\ }\mathrm{1}\mathrm{\ ..\ }\mathrm{3}\right]\]
- الف) در سطر اول به ترتیب: تعداد سطرها (m)، تعداد ستونها (n) و تعداد خانههای مخالف صفر (r) ماتریس اسپارس قرار داده میشود.
- ب) از سطر دوم به بعد، هر سطر شامل سه مؤلفه است که همان مختصات و مقدار خانههای مخالف صفر است: \(\left(\mathrm{i\ ,\ j\ ,\ A}\left[\mathrm{i\ ,\ j}\right]\neq \mathrm{\circ }\right)\)
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
| نمایش ماتریس اسپارس |
| 14 | 0 | 0 | 0 | 13 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 16 | |
| 15 | 0 | 0 | 0 | 0 | 0 | |
| \( 3 \times 6 \) | ||||||
| ماتریس اسپارس | ||||||
چون خانههای مخالف "∘" ، 4 تا است، بنابراین ماتریس اسپارس شامل 5 سطر و 3 ستون خواهد بود.
مقرون به صرفه بودن
روش مطرح شده در بالا در شرایطی مقرون به صرفه است که تعداد خانههای ماتریس نگهدارندهی \(\mathrm{sparse}\left[\mathrm{1}\mathrm{\ ..\ r+}\mathrm{1}\mathrm{\ ,\ }\mathrm{1}\mathrm{\ ..\ }\mathrm{3}\right]\) از تعداد خانههای ماتریس اسپارس \( m \times n \) به مراتب کمتر باشد:
\[\mathrm{3}\left(\mathrm{r\ +\ }\mathrm{1}\right)\mathrm{ <\ mn}{{\stackrel{\mathrm{\ \ \ \ \ \ }\mathrm{3}\left(\mathrm{r\ +\ }\mathrm{1}\right)\ =\ \mathrm{3}\mathrm{r}\ \ \ \ \ \ }{\longrightarrow}}}\mathrm{r\ <\ }\frac{\mathrm{mn}}{\mathrm{3}}\]
به عبارت بهتر تعداد خانههای مخالف صفر r کمتر از \(\frac{\mathrm{1}}{\mathrm{3}}\) خانههای ماتریس اسپارس باشد.
مثال: میتوان هر ماتریس تنک (Sparse) را به صورت یک آرایه دو بعدی نمایش داد. برای این کار سطر، ستون و مقدار درایههای غیرصفر ماتریس را در آرایه ذخیره میکنند. یک ماتریس L قطری با n سطر و n ستون داده شده است. برای مقرون به صرفه بودن این نمایش تنک، بزرگترین L ممکن برابر است با ... (علوم کامپیوتر- کارشناسی ارشد- 79)
| 1) \( L \lt \lfloor \frac{n}{3}\rfloor \) | 2) \( L \lt \lfloor \frac{n}{2}\rfloor \) | 3) \( L \lt \lfloor \sqrt{n}\rfloor \) | 2) \( L \lt \lfloor \frac{n}{4}\rfloor \) |
حل: گزینه 1 درست است.
تعداد خانههای مخالف صفر در یک ماتریس \( n \times n \) به صورت L قطری برابر با \(\mathrm{r\ =\ nL}\mathrm{-}\frac{{\mathrm{L}}^{\mathrm{2}}-\mathrm{1}}{\mathrm{4}}\simeq \mathrm{nL}\) است. بنابراین باید:
\[\mathrm{r\ \lt }\frac{\mathrm{mn}}{\mathrm{3}}{{\mathop{{{\stackrel{\mathrm{\ \ \ \ \ \ m\ =\ n\ \ \ \ \ }}{\longrightarrow}}}}_{\mathrm{r\ =\ nl}}}}\mathrm{nL\ \lt }\frac{\mathrm{n\ \times \ n}}{\mathrm{3}}\to \mathrm{L\ \lt }\frac{\mathrm{n}}{\mathrm{3}}\]
ترانهاده کردن (Transpose) ماتریس اسپارس
برای ترانهاده کردن ماتریس sparse به این شکل عمل میکنیم که ابتدا در سطر اول، جای سطر و ستون را عوض کرده و به همراه تعداد خانههای مخالف صفر در ماتریس ترانهاده قرار میدهیم. سپس از سطر دوم به بعد روی ستون دوم به ترتیب از بالا به پایین کوچکترین عنصر را پیدا کرده، جای سطر و ستون آنها را عوض کرده و به همراه مقدارشان در ماتریس ترانهاده قرار میدهیم.
|
\[\stackrel{\mathrm{\ \ \ \ \ \ \ \ \ \ }\mathrm{\textrm{ترانهاده}}\mathrm{\ \ \ \ \ \ \ \ \ \ \ \ }}{\longrightarrow}\] |
|
تحلیل الگوریتم ترانهاده
برای ترانهاده کردن ماتریس \( A_{ rows \times columns} \) در ماتریس \( B_{ columns \times rows} \) میتوان از الگوریتم زیر در زمان \( O( columns \times rows) \) استفاده کرد:
for i := 1 to columns do
for j := 1 to rows do
B[j][i] := A[i][j];
ترانهاده ماتریس اسپارس
در صورتی که ماتریس اسپارس rows × columns با element خانه مخالف صفر وجود داشته باشد و برای ذخیرهی آن از یک آرایه دو بعدی با 1 + rows سطر و 3 ستون استفاده کنیم، زمان ترانهاده کردن ماتریس (columns × elements)O خواهد شد.
ترانهاده سریع ماتریس اسپارس
با استفاده از یک الگوریتم کاراتر و سریعتر میتوان در زمان (columns + elements)O ترانهاده یک ماتریس اسپارس را به دست آورد. (برای کسب اطلاعات بیشتر به فصل دوم از کتاب ساختمان داده هورویتز ترجمه علیخانزاده مراجعه شود)
مثال: ماتریس خلوت ماتریسی است دو بعدی مانند \(\mathrm{A}\left[\mathrm{1}\mathrm{\ ..\ m\ ,\ }\mathrm{1}\mathrm{\ ..\ n}\right]\) که اکثر عناصر آن صفر میباشد. برای صرفهجویی در حافظه فقط عناصر غیر صفر را به همراه شماره سطر و شماره ستون و مقدار عنصر در آرایهای با تعریف زیر ذخیره مینماییم. (به ترتیب سطری)
\[\mathrm{type\ sparse\ matrix\ =\ arry}\left[\mathrm{\circ }\ ..\ \ \mathrm{max\ terms\ ,\ }\mathrm{1}\mathrm{\ ..\ }\mathrm{3}\right]\mathrm{\ of\ integer}\mathrm{;}\]
کدامیک از گزینههای زیر صحیح میباشد؟ (t تعداد عناصر غیر صفر میباشد.)
- سریعترین زمان برای به دست آوردن ترانهاده ماتریس خلوت به ترتیب سطری O(n + t) است.
- حاصلضرب دو ماتریس خلوت الزاماً یک ماتریس خلوت است.
- سریعترین زمان برای به دست آوردن ترانهاده ماتریس خلوت به ترتیب سطری O(m + t) است.
- سریعترین زمان برای به دست آوردن ترانهاده ماتریس خلوت به ترتیب سطری θ(nt) است.
حل: گزینه 1 درست است.
\[\mathrm{O}\left(\mathrm{columns\ +\ elements}\right){{\stackrel{\mathrm{\ \ \ \ \ \ columns\ =\ n\ ,\ elements\ =\ t\ \ \ \ \ \ }}{\longrightarrow}}}\mathrm{O}\left(\mathrm{n\ +\ t}\right)\]
2- «آرایه یک بعدی برای نگهداری مقادیر مخالف صفر به کمک فرمول (رابطه)» در ماتریسهای بالا مثلث، پایین مثلث، سه قطری و ...
بعضی ماتریسها مانند: بالا مثلث، پایین مثلث و ... اسپارس نیستند، اما زمانی که تعداد عناصر در آنها زیاد میشود، تعداد صفرهای ماتریس قابل توجه خواهد شد در این وضعیت بهتر است مقادیر مخالف صفر ماتریس به صورت زیر ذخیره شود:
الف- یک آرایه یک بعدی برای نگهداری مقادیر مخالف صفر ماتریس به صورت سطری یا ستونی، که تعداد عناصر آرایه یک بعدی به تعداد مقادیر مخالف صفر ماتریس میباشد.
ب- یک رابطه یا فرمول که محل مقادیر مخالف صفر ماتریس را در آرایه یک بعدی مشخص کند.
مثال: ماتریس پایین مثلث \(\mathrm{A}\left[\mathrm{1}\mathrm{..\ n\ ,\ }\mathrm{1}\mathrm{\ ..\ n}\right]\) را در نظر بگیرید که عناصر مخالف صفر آن را به صورت سطری در یک آرایه یک بعدی نگهداری کردهایم در این وضعیت:
1- در ماتریس \(\mathrm{S\ =\ }\frac{\mathrm{n}\left(\mathrm{n\ +\ }\mathrm{1}\right)}{\mathrm{2}}\) خانهی مخالف صفر وجود دارد. برای همین به یک آرایه یک بعدی \(\left(\mathrm{B}\left[\mathrm{1}\mathrm{\ ..\ S}\right.\right)\) نیاز داریم.
2- هر خانه \(\mathrm{A}\left[\mathrm{i\ ,\ j}\right]\neq \mathrm{\circ }\) در ماتریس پایین مثلث با رابطه (فرمول سطری) زیر محل خود را در آرایه یک بعدی \(\left(\mathrm{B}\left[\mathrm{k}\right]\right)\) مشخص میکند.
\[\mathrm{k\ =\ }\frac{\mathrm{i}\left(\mathrm{i}\mathrm{-}\mathrm{1}\right)}{\mathrm{2}}+\mathrm{j}\]
| \(\left(\mathrm{B}\left[\mathrm{k}\right]\right)\) | ||||||||||||||
|
||||||||||||||
| \(\mathrm{S\ =\ }\frac{\mathrm{n}\left(\mathrm{n\ +\ }\mathrm{1}\right)}{\mathrm{2}}\) |
![]()
| \(\mathrm{A}\left[\mathrm{i\ ,\ j}\right]\neq \mathrm{\circ }\) | ||||||||||||||||
|
| \(\left(\mathrm{B}\left[\mathrm{k}\right]\right)\) | ||||||||||||
|
\( \rightarrow \)
| \(\mathrm{A}\left[\mathrm{i\ ,\ j}\right] \) | |||||||||
|
بهطور مثال موقعیت خانهی A[3,2]=50 در آرایه یک بعدی B[5] است. رابطه بین (i=3 , j=2) در ماتریس و (5 = k) در آرایه یک بعدی توسط فرمول زیر تعیین میشود:
\[\mathrm{k\ =\ }\frac{\mathrm{i}\left(\mathrm{i}\mathrm{-}\mathrm{1}\right)}{\mathrm{2}}+\mathrm{j}\]
که در اینجا داریم:
\[\underbrace{\mathrm{A}\left[\mathrm{3}\mathrm{\ ,\ }\mathrm{2}\right]}_{\left[\mathrm{i\ ,\ j}\right]}\underbrace{\mathop{{{\stackrel{\mathrm{\ \ \ \ i\ =\ }\mathrm{3}\mathrm{\ \ \ \ }}{\longrightarrow}}}}_{\mathrm{j\ =\ }\mathrm{2}}\mathrm{k\ =\ }\frac{\mathrm{3}\left(\mathrm{3}\mathrm{-}\mathrm{1}\right)}{\mathrm{2}}+\mathrm{2}\mathrm{\ =\ }\mathrm{5}}_{\frac{\mathrm{i}\left(\mathrm{i}\mathrm{-}\mathrm{1}\right)}{\mathrm{2}}+\mathrm{j}}\mathrm{\longrightarrow }\underbrace{\mathrm{B}\left[\mathrm{5}\right]}_{\mathrm{B}\left[\mathrm{k}\right]}\]
مثال: برای هر خانه مخالف صفر \(\mathrm{A}\left[\mathrm{i\ ,\ j}\right] \) در ماتریس بالا مثلث \( n \times n \) ، رابطه زیر محل آن خانه را در آرایه یک بعدی B مشخص میکند. \(\left(\mathrm{B}\left[\mathrm{k}\right]\right)\)
\[\mathrm{k\ =\ }\left(\mathrm{i}\mathrm{-}\mathrm{1}\right)\left(\mathrm{n}\mathrm{-}\frac{\mathrm{i}}{\mathrm{2}}\right)+\mathrm{j}\]
| فرمول ستونی | فرمول سطری | تعداد خانه مورد نیاز برای ذخیره مقادیر مخالف صفر در آرایه یک بعدی | ماتریس |
| \(\mathrm{k\ =\ }\left(\mathrm{j}\mathrm{-}\mathrm{1}\right)\left(\mathrm{n}\mathrm{-}\frac{\mathrm{j}}{\mathrm{2}}\right)+\mathrm{i}\) | \(\mathrm{k\ =\ }\frac{\mathrm{i}\left(\mathrm{i}\mathrm{-}\mathrm{1}\right)}{\mathrm{2}}+\mathrm{j}\) | \(\frac{\mathrm{n}\left(\mathrm{n\ +\ }\mathrm{1}\right)}{\mathrm{2}}\) | پایین مثلث |
| \(\mathrm{k\ =\ }\frac{\mathrm{j}\left(\mathrm{j}\mathrm{-}\mathrm{1}\right)}{\mathrm{2}}+\mathrm{i}\) | \(\mathrm{k\ =\ }\left(\mathrm{i}\mathrm{-}\mathrm{1}\right)\left(\mathrm{n}\mathrm{-}\frac{\mathrm{i}}{\mathrm{2}}\right)+\mathrm{j}\) | \(\frac{\mathrm{n}\left(\mathrm{n\ +\ }\mathrm{1}\right)}{\mathrm{2}}\) | بالا مثلث |
| \(\mathrm{2}\mathrm{j\ +\ i}\mathrm{-}\mathrm{2}\) | \(\mathrm{2}\mathrm{i\ +\ j}\mathrm{-}\mathrm{2}\) | \(\mathrm{3}\mathrm{n\ -\ 2}\) | سه قطری |
نتیجهگیری:
بین دو روش بیان شده یعنی:
- روش عمومی نمایش ماتریس اسپارس (نگهداری مختصات مقادیر مخالف صفر با استفاده از آرایه 2 بعدی)
- نگهداری مقادیر مخالف صفر در آرایه یک بعدی که تعداد عناصر آن به تعداد خانههای مخالف ∘ است.
روش دوم از نظر حافظه مقرون به صرفهتر است البته به شرط آن که بتوان رابطه یا فرمولی بین اندیسهای آرایه B[k] و اندیسهای مقادیر مخالف صفر A[i,j] پیدا کرد.
مثال: ماتریس دو بعدی با ابعاد \( N \times N \) به نام MAT2 یک ماتریس تنک یا خلوت (Sparse) است که در آن هر سطر فقط عنصر روی قطر، یک عنصر بالای قطر و یک عنصر زیر قطر دارای اطلاع بوده و بقیه عناصر همه صفر میباشند. میخواهیم جهت جلوگیری از هدر رفتن فضا اطلاعات را بهجای این که از ماتریس دو بعدی MAT2 ذخیره نماییم در ماتریس یک بعدی MAT1 به صورت زیر ذخیره کنیم.
\[\mathrm{MAT}\mathrm{2}\left[ \begin{array}{c} {\mathrm{a}}_{\mathrm{11}}\ \ \ \ \ {\mathrm{a}}_{\mathrm{12}}\ \ \ \ \ \mathrm{\circ }\mathrm{\ }\mathrm{\ }\mathrm{\ \ \ \ \ \ }\mathrm{\circ } \\ {\mathrm{a}}_{\mathrm{21}}\ \ \ \ \ {\mathrm{a}}_{\mathrm{22}}\ \ \ \ \ {\mathrm{a}}_{\mathrm{23}}\ \ \ \ \ \ \\ \begin{array}{c} \mathrm{\circ }\ \ \ \ \ \mathrm{\ }\ \ \ {\mathrm{a}}_{\mathrm{32}}\ \ \ \ \ {\mathrm{a}}_{\mathrm{33}}\ \ \ \ \ \ \\ \mathrm{\circ }\ \ \ \ \ \ \mathrm{\ }\ \circ \ \ \ \ \ \ \ \ {\mathrm{a}}_{\mathrm{43}}\ \ \ \ \ \ \\ \mathrm{\circ }\mathrm{\ }\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ddots \end{array} \end{array} \right]\]
| 6 | 5 | 4 | 3 | 2 | 1 | ||
| ... | \( a_{32} \) | \( a_{23} \) | \( a_{22} \) | \( a_{21} \) | \( a_{12} \) | \( a_{11} \) | MAT1 |
عنصر MAT2[i,j] ، \( (i,j \le n) \) در چه خانهای (اندیس) از ماتریس MAT1 ذخیره خواهد شد؟
| 1) \( \frac{\mathrm{I\ \times \ }\left(\mathrm{I}\mathrm{\ -\ }\mathrm{1}\right)}{\mathrm{2}}\mathrm{+}\mathrm{J} \) | 2) \(\mathrm{2}\mathrm{I\ +\ J}\mathrm{-}\mathrm{2}\) |
| 3) \(\mathrm{3}\mathrm{\ \times \ }\left(\mathrm{I\ +\ J}\right)\) | 4) \(\mathrm{3}\mathrm{\ \times }\left(\mathrm{I\ +\ J}\right)-\mathrm{2}\) |
حل: گزینه 2 درست است.
برای به دست آوردن رابطهای که هر خانه مخالف صفر A[i ,j] در ماتریس سه قطری MAT2 را در آرایهی یک بعدی MAT1 ذخیره کند از این روش استفاده میکنیم که چند عنصر به صورت تصادفی از آرایه دو بعدی انتخاب کرده و i، j آن را در روابط گزینهها قرار میدهیم تا ببینیم اندیس به دست آمده از روابط با اندیس خانهها در آرایه یک بعدی همخوانی دارد یا نه.
گزینه 1 :$\frac{\mathrm{2}\mathrm{\ \times \ }\left(\mathrm{2}\mathrm{-}\mathrm{1}\right)}{\mathrm{2}}+\mathrm{3}\mathrm{\ =\ }\mathrm{4}\mathrm{\ }\mathrm{\neq }\mathrm{\ }\mathrm{5}$ ✗
گزینه 2 :$\mathrm{2}\left(\mathrm{2}\right)+\left(\mathrm{3}\right)-\mathrm{2}\mathrm{\ =\ }\mathrm{5}\mathrm{\ =\ }\mathrm{5}$ ✓
گزینه 3 :$\mathrm{3}\mathrm{\ \times }\left(\mathrm{2}\mathrm{\ +\ }\mathrm{3}\right)=\mathrm{15}\mathrm{\ }\mathrm{\neq }\mathrm{\ }\mathrm{5}$ ✗
گزینه 4 :$\mathrm{3}\mathrm{\ \times }\left(\mathrm{2}\mathrm{\ +\ }\mathrm{3}\right)-\mathrm{2}\mathrm{\ =\ }\mathrm{13}\mathrm{\ }\mathrm{\neq }\mathrm{\ }\mathrm{5}$ ✗
مبینا محسنی زاده
ضرب ماتریسها
بر روی هر ماتریس عملیات مختلفی میتواند انجام گیرد. مانند: جمع، تفریق، ضرب ... که یکی از مهمترین آنها عملیات ضرب ماتریسها است.
شرایط ضرب دو ماتریس
برای آن که ضرب دو ماتریس A و B امکانپذیر باشد باید بعد وسط آنها یکسان باشد به عبارت بهتر برای امکانپذیر بودن حاصلضرب $A \times B$ باید ستون ماتریس A با سطر ماتریس B یکسان باشد. در نتیجه:
$\mathrm{C}_{\mathrm{m\ \times\ k}}\ \ \ \ \gets\ \ \ \ \mathrm{A}_{\mathrm{m\ \times\ n}}\times\mathrm{B}_{\mathrm{n\ \times\ k}}$
خواص ضرب ماتریسها
الف) ضرب ماتریسها خاصیت جابهجایی ندارد.$\mathrm{AB\ \neq\ BA}$
ب) ضرب ماتریسها خاصیت شرکتپذیری دارد.
حالتهای شرکتپذیری 4 ماتریس A، B، C و D
1) $(AB)(CD)$
2) $((A(BC))D)$
3) $(A((BC)D))$
4) $(((AB)C)D)$
5) $(A(B(CD)))$
حالتهای شرکتپذیری 3 ماتریس A، B و C
1) $A(BC)$
2) $(AB)C$
محاسبه تعداد حالات شرکتپذیری ضرب ماتریسها
تعداد حالات شرکتپذیری ضرب 1 + n ماتریس برابر عدد کاتالان بوده و از رابطه زیر به دست میآید:
$\frac{\left(\begin{matrix}\mathrm{2n}\\\mathrm{n}\\\end{matrix}\right)}{\mathrm{n\ +\ 1}}$
مثال: تعداد حالات شرکتپذیری ضرب 4 ماتریس کدام است؟
$\mathrm{n\ +\ 1\ =\ 4\ \Rightarrow\ n\ =\ 3\ }\longrightarrow$ تعداد حالات شرکت پذیری ضرب$=\mathrm{\ }\frac{\left(\begin{matrix}\mathrm{6}\\\mathrm{3}\\\end{matrix}\right)}{\mathrm{3\ +\ 1}}\mathrm{=}5$
هر گاه یک ماتریس بالا مثلث را در ماتریس بالا مثلث دیگری ضرب کنیم، حاصل ماتریس بالا مثلث است.
هر گاه یک ماتریس پایین مثلث را در ماتریس پایین مثلث دیگری ضرب کنیم، حاصل ماتریس پایین مثلث است.
هر گاه یک ماتریس قطری را در ماتریس قطری دیگری ضرب کنیم، حاصل ماتریس قطری است.
به عبارت دیگر ضرب یک ماتریس در ماتریس دیگر با همان مشخصه ماتریس اول خاصیت ماتریس را عوض نمیکند.
محاسبه تعداد ضربهای حاصلضرب چند ماتریس
اگر نتیجهی حاصلضرب دو ماتریس$\mathrm{A}_{\mathrm{m\ \times\ n}}\times\mathrm{B}_{\mathrm{n\ \times\ k}}$ را به صورت$\mathrm{C}_{\mathrm{m\ \times\ k}}$در نظر بگیریم آنگاه:
الگوریتم ضرب ($\mathrm{C}_{\mathrm{m\ \times\ k}}=\mathrm{A}_{\mathrm{m\ \times\ n}}\times\mathrm{B}_{\mathrm{n\ \times\ k}}$)
$for i : = 1 \ \ to \ \ m \ \ do $
$for j : = 1 \ \ to \ \ k\ \ do $
$begin$
$\mathrm{C}\left[\mathrm{i\ ,\ j}\right]=\mathrm{\circ;}$
$for l : = 1 \ \ to \ \ n \ \ do $
$\mathrm{C}\left[\mathrm{i\ ,\ j}\right]:=\ \mathrm{C}\left[\mathrm{i\ ,\ j}\right]+\mathrm{A}\left[\mathrm{i\ ,\ L}\right]^{\ \ast\ }\mathrm{B}\left[\mathrm{L\ ,\ j}\right];$
$end;$
تعداد ضربهای انجام شده $ m × n × k=$
تعداد جمعهای انجام شده $ m × n × k=$
دقت کنید:
اگر دو ماتریس$\ \mathrm{A}_{\mathrm{m\ \times\ n}}$ و $\mathrm{B}_{\mathrm{n\ \times\ k}}$ ا در هم ضرب کنیم تعداد جمعها$\mathrm{m}\left(\mathrm{n}-\mathrm{1}\right)\mathrm{k} $میشود اما چون در کامپیوتر این جمعها باید در ماتریس$\mathrm{C}_{\mathrm{m\ \times\ k}} $که ماتریس حاصل از ضرب دو ماتریس است قرار گیرد، یک جمع نیز به ازای هر خانه $\mathrm{C}_{\mathrm{m\ \times\ k}}$اضافه میشود که در نهایت$\mathrm{m}\left(\mathrm{n}-\mathrm{1}\right)\mathrm{k\ +\ mk}$ جمع خواهیم داشت که همان mnk است. (قبل از انجام ضرب تمام خانههای ماتریس$\mathrm{C}_{\mathrm{m\ \times\ k}}$را قرار میدهیم.)
مثال 1: تعداد ضربهای حاصلضرب 3 ماتریس$\mathrm{C}_{\mathrm{5\ \times\ 4}}$ ،$\mathrm{B}_{\mathrm{10\ \times\ 5}}$ ، $\mathrm{A}_{\mathrm{3\ \times\ 10}}$با توجه به حالتهای مختلف شرکتپذیری کدام است؟
$\mathrm{A}_{\mathrm{3\ \times\ 10}}\left(\mathrm{BC}\right)_{\mathrm{10\ \times\ 4}}=\left(\mathrm{3\ \times\ 10\ \times\ 4}\right)+\left(\mathrm{10\ \times\ 5\ \times\ 4}\right)=\mathrm{120\ +\ 200\ =\ \ 320}$
$\left(\mathrm{AB}\right)_{\mathrm{3\ \times\ 5}}\mathrm{C}_{\mathrm{5\ \times\ 4}}=\left(\mathrm{3\ \times\ 10\ \times\ 5}\right)+\left(\mathrm{3\ \times\ 5\ \times\ 4}\right)=\mathrm{150\ +\ 60\ =\ 210}$
دیده میشود که حالتهای مختلف شرکتپذیری، تعداد ضربهای متفاوتی به وجود میآورد.
محاسبه بهینهترین تعداد ضرب در ضرب چند ماتریس
در ضرب چند ماتریس بهینهترین حالت در مورد تعداد ضربها داشتن کمترین تعداد ضرب است تا عمل ضرب ماتریسها سریعتر انجام شود.
قضیه: در هنگام ضرب 3 ماتریس $\mathrm{A}_{\mathrm{m\ \times\ n}}$ , $ {\mathrm{B}_{\mathrm{n\ \times\ k}}\mathrm{C} }_{\mathrm{k\ \times\ L}}$برای آن که:
تعداد ضرب (AB)C < تعداد ضرب A(BC)$\longleftrightarrow\frac{\mathrm{1}}{\mathrm{m}}+\frac{\mathrm{1} }{\mathrm{k}}>\frac{\mathrm{1} }{\mathrm{n}}+\frac{\mathrm{1} }{\mathrm{L}}$
نتیجه: طبق یک قاعده سرانگشتی میتوان گفت که هنگام ضرب چند ماتریس، اگر ماتریسهایی را زودتر ضرب کنیم که بُعد وسط آنها بزرگتر و بعد کناری آنها به نسبت کوچکتر است، بدین ترتیب تعداد ضربها کوچکتر میشود.
تحلیل مثال 1:
در هنگام ضرب ماتریسهای$\mathrm{A}_{\mathrm{3\ \times\ 10}}\times\mathrm{B}_{\mathrm{10\ \times\ 5}}\times\mathrm{C}_{\mathrm{5\ \times\ 4}}$از آنجاییکه$\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1} }{\mathrm{5}}>\frac{\mathrm{1} }{\mathrm{10}}+\frac{\mathrm{1} }{\mathrm{4}}$در نتیجه تعداد ضربهای (AB)C کمتر از تعداد ضربهای A(BC) است. در اینجا بعد وسط AB بزرگتر بود.
مثال 2: اگر A یک ماتریس$5\times 13$ ، B ماتریس $89\times5$ ، C ماتریس $3\times89$ و D یک ماتریس $34\times3$ باشد کمترین تعداد ضرب برای به دست آوردن حاصلضرب $A \times B \times C \times D $چقدر است؟
حل: گزینه 2 درست است.
تعداد ضرب ها
$\mathrm{5\ \times\ 89\ \times3\ =\ 335}$
$\mathrm{13\ \times\ 5\ \times3\ =\ 195}$
$\mathrm{13\ \times\ 3\ \times\ 34\ =\ 1326}$
ترتیب (شرکتپذیری) ماتریسها برای داشتن کمترین ضرب
$\mathrm{B}_{\mathrm{5\ \times\ 89}}\times\mathrm{C}_{\mathrm{89\ \times\ 3}}=\left(\mathrm{B\ \times\ C}\right)_{\mathrm{5\ \times\ 3}}$
$\mathrm{A}_{\mathrm{13\ \times\ 5}}\times\left(\mathrm{B\ \times\ C}\right)_{\mathrm{5\ \times\ 3}}=\left(\mathrm{A\ \times\ }\left(\mathrm{B\ \times\ C}\right)\right)_{\mathrm{13\ \times\ 3}}$
$\left(\mathrm{A\ \times\ }\left(\mathrm{B\ \times\ C}\right)\right)_{\mathrm{13\ \times\ 3}}\times\mathrm{D}_{\mathrm{3\ \times\ 34}}=\left(\left(\mathrm{A}\left(\mathrm{BC}\right)\right)\mathrm{D} \right)_{\mathrm{13\ \times\ 34}}$
2856 = جمع ضربها
مثال 3: میخواهیم برای ماتریسهای$\mathrm{M}_{\mathrm{1}_{\left(\mathrm{10\ \times\ 20}\right)}}$ و $\mathrm{M}_{\mathrm{2}_{\left(\mathrm{20\ \times\ 50}\right)}}$ و $\mathrm{M}_{\mathrm{3}_{\left(\mathrm{50\ \times\ 1}\right)}} $ و $\mathrm{M}_{\mathrm{4}_{\left(\mathrm{1\ \times\ 100}\right)}}$ترکیب بهینه پرانتزبندی پیدا نماییم تا تعداد ضربهای کل جهت محاسبه عبارت ذیل حداقل گردد:
$\mathrm{M\ =\ }\mathrm{M}_\mathrm{1}\times\mathrm{M}_\mathrm{2}\times\mathrm{M}_\mathrm{3}\times\mathrm{M}_\mathrm{4}$
این ترکیب بهینه عبارت است از؟
حل: گزینه 1 درست است.
نکته مهم: اگر در صورت یک مسئله برای ضرب چند ماتریس، بهینه بودن (تعداد ضرب کمتر- سرعت اجرا) مطرح نباشد، ماتریسها را از سمت چپ به راست پشت سر هم ضرب میکنیم.
بهطور مثال در ضرب ماتریسهای$\mathrm{A}_{\mathrm{m\ \times\ n}}\times\mathrm{B}_{\mathrm{n\ \times\ k}}\times\mathrm{C}_{\mathrm{k\ \times\ L}}$پیشفرض حاصلضرب را به صورت (AB)C در نظر میگیریم.
مثال 4: قطعه برنامه زیر برای ضرب دو ماتریس مربع A و B با مرتبه n مورد نظر است:
(کارشناسی ارشد- علوم کامپیوتر 79)
برای تکمیل این قطعه برنامه، دستور حذف شده به صورت ..................... است.
$\mathrm{for\ \ i∶\ =\ 1\ \ \ to\ \ \ n\ \ \ do}$
$\mathrm{for\ \ j∶\ =\ 1\ \ \ to\ \ \ n\ \ \ do\ \ \ begin}$
$\mathrm{\ c}\left[\mathrm{i\ ,\ j}\right]\mathrm{∶\ =\ \circ;}$
$\mathrm{for\ \ k∶\ =\ 1\ \ \ to\ \ \ n\ \ \ do}$
دستورات حذف شده
end:
حل: گزینه 1 درست است.
جستجو در آرایهها
بهطور کلی برای جستجوی یک عنصر دلخواه در آرایهها 2 روش اساسی وجود دارد:
- روش جستجوی خطی (ترتیبی)
- روش جستجوی دودویی (باینری)
1- روش جستجوی خطی (ترتیبی)
در این روش برای جستجوی دادهی x در آرایه n تایی $\mathrm{A}\left[\mathrm{1\ ..\ n}\right]$، جستجو را از یکی از دو طرف آرایه (پیشفرض از ابتدا) آغاز میکنیم و داده مورد نظر را پشت سر هم با عناصر آرایه مقایسه میکنیم، تا این که یا داده مورد نظر پیدا شود یا به طرف دیگر آرایه (انتهای آرایه) برسیم.
الگوریتم جستجوی خطی
برای پرسوجوی (جستجوی) داده x در آرایه n تایی $\mathrm{A}\left[\mathrm{1\ ..\ n}\right]$:
$flag : = false;$
$\mathrm{For\ \ i∶\ =\ 1\ \ \ to\ \ \ n\ \ \ do}$
$\ \ \mathrm{if\ }\left(\mathrm{A}\left[\mathrm{i}\right]=\mathrm{x} \right)\mathrm{\ then}$
$begin$
$Flag : = True;$
$break;$
$end;$
$if Flag = True then$
$write (' Location is:' , i) ;$
$else$
$write (' not found');$
در صورتی که شرط if برقرار شود$\left(\mathrm{x\ =\ A}\left[\mathrm{i}\right]\right)$عنصر x پیدا شده و محل آن i است در نتیجه Flag، True شده از حلقه خارج میشویم.
دقت کنید: در روش جستجوی خطی چون هیچ استراتژی خاصی جز جستجوی پشت سر هم از ابتدا تا انتها وجود ندارد، در نتیجه sort بودن یا نبودن آرایه تأثیری در روند جستجو ندارد.
تحلیل جستجوی خطی
در الگوریتم جستجوی خطی مهمترین پارامتر، مقایسه است، در نتیجه تعداد مقایسات مهمترین عامل در محاسبه مرتبه اجرایی الگوریتم جستجوی خطی به حساب میآید.
الف) بهترین حالت: داده مورد جستجو (x) در ابتدای لیست باشد (با فرض شروع جستجو از ابتدا). در این حالت حداقل مقایسه را داریم.
ب) بدترین حالت: داده مورد جستجو (x) در انتهای لیست باشد (با فرض شروع جستجو از ابتدا). در این حالت حداکثر مقایسه را داریم.
ج) حالت متوسط: متوسط مقایسات برابر است با: $\frac{ \textrm{مجموع مقایسات} }{ \textrm{تعداد عناصر آرایهها} }$
در حالت کلی اگر داده x عنصر اول آرایه باشد با 1 مقایسه، اگر عنصر دوم باشد با 2 مقایسه و ... و اگر عنصر n ام باشد با n مقایسه به دست میآید، در نتیجه:
مجموع مقایسات= $\mathrm{1\ +\ 2\ +\ \ldots\ +\ n\ =\ }\frac{\mathrm{n}\left(\mathrm{n\ +\ 1}\right)}{\mathrm{2}}\ \rightarrow \textrm{زمان}=o(n)$
متوسط= $\frac{\frac{\mathrm{n}\left(\mathrm{n\ +\ 1}\right)}{\mathrm{2}}}{\mathrm{n}}=\ \frac{\mathrm{n\ +\ 1} }{\mathrm{2}}\ \rightarrow \textrm{ مقایسه}$
نتیجهگیری جستجوی خطی:
| بهترین حالت | حالت متوسط | بدترین حالت |
| حداقل مقایسه 1 در زمان (1)O | O(n)مقایسه در زمان$\frac{\mathrm{n\ +\ 1}}{\mathrm{2}}$ | حداکثر مقایسه n در زمان O(n) |
مرتبه اجرایی جستجوی خطی
در الگوریتم جستجوی خطی مهمترین پارامتر، مقایسه است، در نتیجه تعداد مقایسه مهمترین عامل در محاسبه مرتبه اجرایی الگوریتم جستجوی خطی به حساب میآید. زمان جستجوی خطی یا به عبارت بهتر مرتبه اجرایی آن مربوط به حالت متوسط بوده و برابر با O(n) است.
2- جستجوی دودویی (Binary Search)
شرط اولیه در این روش جستجو مرتب (sort) بودن آرایه (پیشفرض صعودی) است، در غیر این صورت این روش غیرقابل استفاده و تعریف نشده خواهد بود.
روش جستجو
داده مورد جستجو (x) را با خانه میانی$\mathrm{A}\left[\mathrm{mid}\right]$آرایه مقایسه میکنیم، در صورتی که با آن خانه برابر باشد جستجو پایان میپذیرد در غیر این صورت در صورتی که $\mathrm{x\ \gt\ A}\left[\mathrm{mid}\right]$باشد به نیمه بالای آرایه میرویم و در صورتی که$\mathrm{x\ \lt\ A}\left[\mathrm{mid}\right]$باشد به نیمه پایین آرایه میرویم و دوباره با قسمت میانی آن نیمه عمل مقایسه را انجام میدهیم این عمل را تا زمانی انجام میدهیم که یا به داده مورد نظر برسیم که محل آن mid خواهد بود یا این که داده x در آرایه وجود ندارد که در این صورت Low (اندیس پایین نیمه آرایه) از high (اندیس بالای نیمه آرایه) بیشتر میشود.
الگوریتم جستجوی دودویی
داده جستجو شونده = x
پیشفرض False و در صورت پیدا شدن x، True میشود = Flag
اندیس پایین آرایه = Low
اندیس بالای آرایه = High
آرایه n تایی مرتب صعودی =$\mathrm{A}\left[\mathrm{1}\ldots\ \mathrm{n}\right]$
اندیس وسط آرایه که عامل مقایسه x با$\mathrm{mid\ =\ }\left\lfloor\frac{\mathrm{low\ +\ high}}{\mathrm{2}}\right\rfloor=\textrm{است}\mathrm{A}\left[\mathrm{mid}\right]$
الگوریتم (غیربازگشتی)
$Low:= 1;$
$high: = n ;$
$Flag: = False;$
$\mathrm{while\ }\left(\mathrm{low\ \le\ high}\right)\ \mathrm{AND\ }\left(\mathrm{Flag\ \lt\gt\ True}\right)\mathrm{\ do}$
$begin$
$mid : = (low + high) Div2;$
$\mathrm{if}\left(\mathrm{A}\left[\mathrm{mid}\right]=\mathrm{x} \right)\ \mathrm{then}$
$Flag: = True$
$\mathrm{else\ if\ }\left(\mathrm{x\ \lt\ A}\left[\mathrm{mid}\right]\right)\ \mathrm{then}$
$High:=mid-1$
$\mathrm{else\ if\ }\left(\mathrm{x\ >\ A}\left[\mathrm{mid}\right]\right)\ \mathrm{then}$
$low:=mid+1$
$end;$
الگوریتم (بازگشتی)
$procedure binary search (a: elementary; x: element; var Low , High, j: integer);$
$var$
$mid: integer;$
$begin$
$\mathrm{if\ }\left(\mathrm{Low\ \le\ High}\right)\mathrm{\ then}$
$begin$
$mid: = (Low + High) Div2$
$\mathrm{case\ compare\ }\left(\mathrm{x\ ,\ a}\left[\mathrm{mid}\right]\right)\ \mathrm{of}$
$\mathrm{'\gt':\ binary\ search\ (a\ ,\ x\ ,\ mid\ +\ 1\ ,\ High\ ,\ j);}$
$\mathrm{'\lt':\ binary\ search\ (a\ ,\ x\ ,\ Low\ ,\ mid}-\mathrm{1\ ,\ j);}$
$'= ' : j: = mid;$
$end;$
$end;$
مثال:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | |
| 3 | 2 | 1 |
| Flag | x | $\mathrm{A}\left[\mathrm{mid}\right]$ | mid | high | Low |
| False | 10 | 40 | 4 | 8 | 1 |
| False | 10 | 20 | 2 | 3 | 1 |
| True | 10 | 10 | 1 | 1 | 1 |
Flag مقدار True گرفته بنابراین محل عنصر mid=1 ,x است
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | |
| 1 | 2 | 3 |
| Flag | x | $\mathrm{A}\left[\mathrm{mid}\right]$ | mid | high | Low |
| False | 75 | 40 | 4 | 8 | 1 |
| False | 75 | 60 | 6 | 8 | 5 |
| False | 75 | 70 | 7 | 8 | 7 |
| False | 75 | 80 | 8 | 8 | 8 |
| False | $\left(\mathrm{Low\ >\ high}\right)$ | 7 | 8 | ||
شرط اتمام حلقه اتفاق افتاده و Flag مقدار False داشته در نتیجه x در آرایه وجود ندارد.
تحلیل الگوریتم
به آرایه زیر و تعداد مقایسهی به دست آمده از جستجوهای موفق و ناموفق دقت کنید:
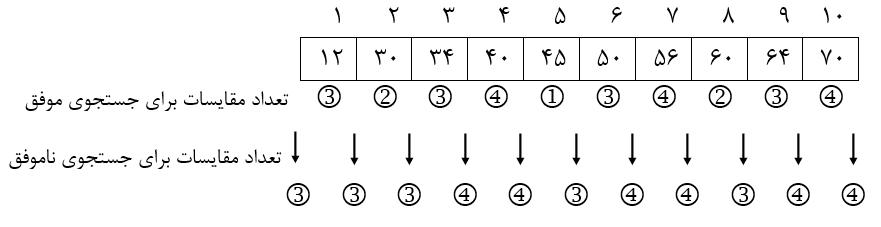
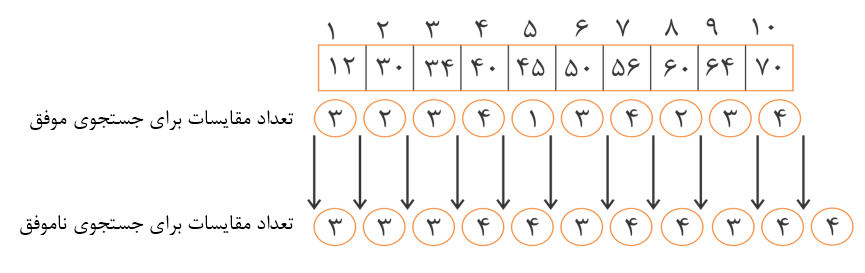
بهطور مثال در جستجوی موفق:
$x=45$با 1 مقایسه به دست میآید.
40,56,70 = x هر کدام با $\left\lfloor\log_\mathrm{2}{\mathrm{10}}\right\rfloor\mathrm{+1\ =\ 4}$مقایسه به دست میآیند.
بهطور مثال در جستجوی ناموفق:
$x=20$بین 12,30 با $\left\lfloor\log_\mathrm{2}{\mathrm{10}}\right\rfloor=\mathrm{3} $مقایسه ناموفق تمام میشود.
$x=66$ بین 64,70 با$ \left\lfloor\log_\mathrm{2}{\mathrm{10}}\right\rfloor+\mathrm{1}=\mathrm{4} $مقایسه ناموفق تمام میشود.
جستجوی موفق
- حداقل تعداد مقایسه: 1
- حداکثر تعداد مقایسه:$\left\lfloor\log_\mathrm{2}{\mathrm{n}}\right\rfloor+\mathrm{1}$
- اگر x در$\mathrm{A}\left[\mathrm{1\ ..\ N}\right]$باشد، همواره با حداکثر$\mathrm{O}\left(\log_\mathrm{2}{\mathrm{N}}\right)$ پیدا میشود.
- در جستجوی موفق برای دو مقدار متفاوت تعداد مقایسههای لازم لزوماً برابر نیست.
جستجوی ناموفق
- حداقل تعداد مقایسه: $\left\lfloor\log_\mathrm{2}{\mathrm{n}}\right\rfloor$
- حداکثر تعداد مقایسه: $\left\lfloor\log_\mathrm{2}{\mathrm{n}}\right\rfloor+\mathrm{1}$
- اگر x در$\mathrm{A}\left[\mathrm{1\ ..\ N}\right]$نباشد، همواره با حداکثر$\mathrm{O}\left(\log_\mathrm{2}{\mathrm{N}}\right)$ مشخص میشود.
- در جستجوی ناموفق برای دو مقدار متفاوت تعداد مقایسههای لازم لزوماً برابر نیست.
s(n) متوسط تعداد مقایسهها برای جستجوی موفق
u(n)متوسط تعداد مقایسهها برای جستجوی ناموفق
با توجه به مثال بالا داریم:
$\mathrm{s}\left(\mathrm{n}\right)=\frac{\textrm{ مجموع مقایسات موفق}}{n}=\frac{29}{10}$
$\mathrm{u}\left(\mathrm{n}\right)=\frac{\textrm{ مجموع مقایسات ناموفق}}{n+1}=\frac{39}{11}$
نتایج:
الف- همواره:
n - مجموع مقایسات ناموفق = مجموع مقایسات موفق
ب- همواره بین s(n),u(n) رابطهی زیر برقرار است:
$ \bbox[5px,border:1px solid black] {\mathrm{s}\left(\mathrm{n}\right)=\left(\mathrm{1\ +\ }\frac{\mathrm{1}}{\mathrm{n}}\right)\mathrm{u}\left(\mathrm{n}\right)-\mathrm{1} }$
زیرا:
$\mathrm{s}\left(\mathrm{n}\right)=\frac{\left(\mathrm{n\ +\ 1}\right)\mathrm{u} \left(\mathrm{n}\right)-\mathrm{n} }{\mathrm{n}}=\frac{\left(\mathrm{n\ +\ 1}\right)\mathrm{u} \left(\mathrm{n}\right)}{\mathrm{n}}-\frac{\mathrm{n} }{\mathrm{n}}=\left(\mathrm{1\ +\ }\frac{\mathrm{1}}{\mathrm{n}}\right)\mathrm{u}\left(\mathrm{n}\right)-\mathrm{1}$
ج- با توجه به قسمت (ب) همواره
$ \bbox[5px,border:1px solid black] { \mathrm{s}\left(\mathrm{n}\right)=\theta\left(\mathrm{u}\left(\mathrm{n}\right)\right) }$
مثال 1: اگر s(n) متوسط تعداد مقایسهها برای جستجوی موفق در یک آرایه مرتب با طول n و u(n) متوسط تعداد مقایسهها برای جستجوی ناموفق در این آرایه با استفاده از روش دودویی باشد، کدامیک از گزینههای زیر نادرست است؟ (سراسری 83- IT)
1)$\mathrm{s}\left(\mathrm{n}\right)=\theta\left(\mathrm{u}\left(\mathrm{n}\right)\right)$
2)$\mathrm{s}\left(\mathrm{n}\right)=\mathrm{u}n-1$
3)$\mathrm{s}\left(\mathrm{n}\right)=\left(\mathrm{1\ +\ }\frac{\mathrm{1}}{\mathrm{n}}\right)\mathrm{u}\left(\mathrm{n}\right)-\mathrm{1}$
4) موارد 1 و 3 صحیح میباشد.
حل: گزینه 2 درست است.
مثال 2: کدامیک از گزینههای زیر در مورد الگوریتم فوق برای جستجوی دودویی در$\mathrm{A}\left[\mathrm{1\ ..\ N}\right]$غلط است؟
(منظور از مقایسه، مقایسه x با یک عنصر از A است.) (سراسری نرمافزار 77)
1) اگر x در$\mathrm{A}\left[\mathrm{1\ ..\ N}\right]$باشد، همواره با حداکثر $\mathrm{O}\left(\log_\mathrm{2}{\mathrm{N}}\right)$پیدا میشود.
2) اگر x در $\mathrm{A}\left[\mathrm{1\ ..\ N}\right]$نباشد، پاسخ false همواره با حداکثر $\mathrm{O}\left(\log_\mathrm{2}{\mathrm{N}}\right)$مقایسه به دست میآید.
3) در جستجوی ناموفق برای دو مقدار متفاوت x (که در A موجود نیستند) همواره تعداد مقایسهها برابر است.
4) حداکثر تعداد مقایسهها (چه موفق و چه ناموفق) همواره از O(N) کمتر است.
حل: گزینه 3 درست است.
محاسبه متوسط مقایسه در جستجوی موفق s(n)
به آرایه زیر و تعداد مقایسهی به دست آمده از جستجوهای موفق دقت کنید:


برای محاسبه متوسط تعداد مقایسات در روش جستجوی دودویی 2 روش وجود دارد.
روش اول:
متوسط تعداد مقایسهها =$\frac{\textrm{ مجموع مقایسات}} {\textrm{ تعداد عناصر آرایه}}=\frac{3+2+3+4+1+3+4+2+3+4}{10}=\frac{29}{10}=2.9$
روش دوم:
یک درخت دودویی کامل به تعداد عناصر آرایه تشکیل داده و به شکل زیر عمل میکنیم:
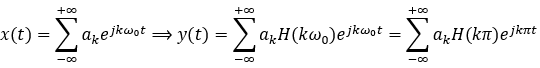
متوسط مقایسه ها برابر است با:
متوسط تعداد مقایسات=$\frac{\Sigma \textrm{شماره سطح ام i ام}\times \textrm{ تعداد گره سطح i} }{\textrm{ تعداد عناصر ارایه}}=\frac{\mathrm{1\ \times1\ +2\ \times2\ +3\ \times4\ +4\ \times3}}{\mathrm{10}}=\frac{\mathrm{29}}{\mathrm{10}}=\mathrm{2.9}$
تحلیل حالت متوسط: متوسط تعداد مقایسه همواره کمتر از$\left\lfloor\log_\mathrm{2}{\mathrm{n}}\right\rfloor+\mathrm{1}$بوده و زمان در این حالت حداکثر$\mathrm{O}\left(\log_\mathrm{2}{\mathrm{n}}\right)$خواهد بود.
مثال: اگر A آرایهای مرتب از اعداد صحیح 1 تا 1024 باشد، الگوریتم جستجوی دودویی با چند بار تکرار عدد 4 را پیدا میکند؟
بار اول با مقایسه عدد 4 با وسط آرایه متوجه میشویم که عدد مذکور باید مابین خانههای 1 تا 512 یعنی نیمه پایینی آرایه باشد به همین ترتیب:
| شمارهی مقایسه | عدد 4 در کدام محدوده است؟ |
| 1 | 1تا512 |
| 2 | 1تا256 |
| 3 | 1تا128 |
| 4 | 1تا64 |
| 5 | 1تا32 |
| 6 | 1تا16 |
| 7 | 1تا8 |
پس از 7 بار تکرار الگوریتم آرایه زیر در نظر گرفته میشود:
| low | mid | high | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
$\mathrm{mid\ =\ }\left\lfloor\frac{\mathrm{1\ +\ 7}}{\mathrm{2}}\right\rfloor=\mathrm{4}$
بار هشتم هنگامی که عدد 4 با محتوای mid مقایسه میشود، پیدا میگردد پس الگوریتم 8 بار تکرار میشود.
مرتبه اجرایی جستجوی دودویی
در الگوریتم جستجوی باینری مهمترین پارامتر، مقایسه است، در نتیجه تعداد مقایسه مهمترین عامل در محاسبه مرتبه اجرایی الگوریتم جستجوی باینری به حساب میآید. زمان جستجوی دودویی یا به عبارت بهتر مرتبه اجرایی آن مربوط به حالت متوسط بوده و برابر با $\mathrm{O}\left(\log_\mathrm{2}{\mathrm{n}}\right)$است.
| بهترین حالت | حالت متوسط | بدترین حالت |
| حداقل مقایسه 1 در زمان (1)O | کمتر از $\left\lfloor\log_\mathrm{2}{\mathrm{n}}\right\rfloor+\mathrm{1}$در زمان $\mathrm{O}\left(\log_\mathrm{2}{\mathrm{n}}\right)$ | حداکثر مقایسه$\left\lfloor\log_\mathrm{2}{\mathrm{n}}\right\rfloor+\mathrm{1} $درزمان $\mathrm{O}\left(\log_\mathrm{2}{\mathrm{n}}\right)$ |
دیده میشود که روش جستجوی دودویی به مراتب از روش جستجوی خطی از نظر تعداد مقایسه بهتر و مقرون به صرفهتر است.
مثال 4: یک آرایه n تایی A از اعداد صحیح، با شرطهای زیر داده شده است: (کارشناسی ارشد- دولتی 79)
1- $ \mathrm{x\ \lt\ y\ ,\ A}\left(\mathrm{n}\right)=\mathrm{y\ ,\ A}\left(\mathrm{1}\right)=\ \mathrm{x}$
2- برای هرi،$ \left|\mathrm{A}\left(\mathrm{i}\right)-\mathrm{A} \left(\mathrm{i\ +\ 1}\right)\right|\le\mathrm{1}$
یک الگوریتم کارا برای جستجوی $\left(\mathrm{x\ \le\ w\ \le\ y}\right)\mathrm{w}$در آرایه A طراحی شده است. این الگوریتم اندیس w را در صورت وجود به دست میآورد. پیچیدگی این الگوریتم در بدترین حالت و حالت متوسط چیست؟
1) بدترین حالت O(n)، حالت متوسط$ O(log n)$
2) بدترین حالت $O(n log n)$ و حالت متوسط O(n)
3) هر دو حالت O(n)
4) هر دو حالت$ O(log n)$
حل: گزینه 3 درست است.
به نظر میآید که آرایهی A مرتب است، در حالی که مثال زیر این نظر را رد میکند.
$\mathrm{x\ =\ \circ}$ و $y=1$واضح است که $\mathrm{x\ \lt\ y}$
| A | 0 | -1 | 0 | 1 |
بنابراین آرایهی A لزوماً مرتب نیست و برای یافتن w باید از جستجوی خطی استفاده کرد.
البته گزینه 4 به عنوان کلید سؤال اعلام شده بود.
مثال 5: فرض کنید یک آرایه 200 عنصری مرتب شده باشد. زمان اجرای بدترین ((n)F) برای پیدا کردن عنصر معلوم X در آرایه A با استفاده از جستجوی دودویی چیست؟ (کارشناسی ارشد- 77)
حل: گزینه 2 درست است.
بدترین حالت تعداد مقایسات برای پیدا کردن عنصر معلوم X در آرایه A برابر است با:
$\left[\log_\mathrm{2}{\mathrm{200}}\right]+\mathrm{1\ =\ 7\ +\ 1\ =\ 8}$
پیدا کردن ماکزیمم و مینیمم در آرایه n عضوی
تعداد مقایسات برای یافتن مینیمم برابر با $n-1$ است.
تعداد مقایسات برای یافتن ماکزیمم برابر با$n-1$ است.
تعداد مقایسات برای یافتن ماکزیمم و مینیمم برابر با:
| n زوج | n فرد |
| $\frac{\mathrm{3n}}{\mathrm{2}}-\mathrm{2}$ | $\frac{\mathrm{3n}}{\mathrm{2}}-\frac{\mathrm{3} }{\mathrm{2}}$ |
مثال 1: مینیمم و ماکزیمم اعداد ذخیره شده در یک آرایه یک بعدی با n خانه، با چند مقایسه بین اعداد ذخیره شده در این خانهها به دست خواهد آمد؟ (کارشناسی ارشد- آزاد 71- آزاد 72 و آزاد 79)
حل: گزینه 2 درست است.
مثال 2: الگوریتم زیر برای پیدا کردن عناصر ماکزیمم و مینیمم یک آرایه با n عنصر پیشنهاد شده است:
(کارشناسی ارشد- دولتی 75)
$procedure min max (i , j: integer ; var min , max : real);$
$var k : integer;$
$min 1 ,min2, max 1, max2, real;$
$begin$
$if \ i+1=j then$
$begin$
$\underline{\mathrm{A}\left[\mathrm{i}\right]>\mathrm{A} \left[\mathrm{j}\right]}$
$begin$
$\mathrm{min∶\ =\ A}\left[\mathrm{j}\right];$
$\mathrm{max∶\ =\ A}\left[\mathrm{i}\right];$
$end$
$else begin$
$\mathrm{min∶\ =\ A}\left[\mathrm{j}\right];$
$\mathrm{max∶\ =\ A}\left[\mathrm{i}\right];$
$end$
$else begin$
$\mathrm{k∶\ =\ }\left(\mathrm{i\ +\ j}\right)\mathrm{div\ 2;}$
$\mathrm{min\ max\ }\left(\mathrm{i\ ,\ k\ ,\ min\ 1\ ,\ max\ 1}\right);$
$\mathrm{min\ max\ }\left(\mathrm{k\ +\ 1\ ,\ j\ ,\ min\ 2\ ,\ max\ 2}\right);$
$\rightarrow\left\{\ \ \ \mathrm{if\ }\underline{\mathrm{min\ 1\ \lt\ min\ 2}}\ \mathrm{then\ min∶=\ min\ 1} \right.$
$else min : = min2 ;$
$\rightarrow\left\{\ \ \ \mathrm{if\ }\underline{\mathrm{max\ 1\ \lt\ max\ 2}}\ \mathrm{then\ max∶=\ max\ 2} \right.$
$ else \ max : = max1$
$end$
$end;$
تعداد مقایسههای این الگوریتم (فقط مقایسههایی که زیر آنها خط کشیده شده است) برای $n=8$چقدر است؟
حل: گزینه 3 درست است.
با استفاده از رابطه$\frac{\mathrm{3n}}{\mathrm{2}}-\mathrm{2}$
$\mathrm{n\ =\ 8\ \ \ \ \rightarrow\ \ \ \ }\frac{\mathrm{3n}}{\mathrm{2}}-\mathrm{2\ =\ }\frac{\mathrm{3} \left(\mathrm{8}\right)}{\mathrm{2}}-\mathrm{2\ =\ 12}-\mathrm{2\ =\ 10}$ = تعداد مقایسات
نکته: الگوریتم فوق فقط برای یافتن عناصر مینیمم و ماکزیمم یک آرایه با$\left(\mathrm{k\ \in\ N}\right)\ \ \mathrm{n\ =\ }\mathrm{2}^\mathrm{k}$کاربرد دارد.
Stack (پشته)
هر لیستی از دادهها که عمل حذف (pop) و درج (push) در آن از یک طرف (بالای پشته) به کمک اشارهگری به نام ʼʼtopʻʻ انجام میگیرد.
پیادهسازی:
برای ذخیرهسازی ساختار یک پشته میتوان یکی از 2 ساختار زیر را در نظر گرفت:
- آرایه (Array): که ساختاری ایستا (static) و محدود دارد.
- لیست پیوندی (Linked List): که ساختاری پویا (dynamic) و متناسب با دادهها دارد.
اشارهگر top و شرایط مرزی (خالی یا پر بودن stack)
در صورتی که از آرایه $\mathrm{stack\ }\left[\mathrm{1\ ..\ n}\right]$
رای نگهداری عناصر پشته استفاده شود، شرایط مرزی به صورت زیر خواهد بود:
| وضعیت top | پشته خالی (empty) | پشته پر (Full) | ||||||||||||||||||||||||||
| آخرین خانه پر (پیشفرض) |
|
|
||||||||||||||||||||||||||
| اولین خانه خالی |
|
|
نکته مهم: همیشه بهطور پیشفرض top به آخرین خانه پر اشاره میکند
الگوریتمهای pop (حذف) و push (درج)
| وضعیت top | الگوریتم (درج) | الگوریتم (حذف) | |||||||||||||||||
|
procedure push (var item : data type); begin if $\mathrm{top\ =\ n} $then write ('stack is Full') else begin ;1 + top : = top stack [top] : = item; end; |
procedure pop (var item : data type); begin if$\mathrm{top\ =\ \circ} $then write ('stack is Empty') else begin item : = stack [top]; $top=top-1$ end; |
|||||||||||||||||
|
procedure push (var item : data type); begin if $\mathrm{top\ =\ n\ +\ 1} $then write ('stack is Full') else begin stack [top] : = item; top=top+1; end; |
procedure pop (var item : data type); begin if $\mathrm{top\ =\ 1} $then write ('stack is Empty') else begin top=top-1; item : = stack [top]; end; |
بهینهسازی قرار گرفتن دو stack در یک آرایه:
در صورتی که بخواهیم دو Stack را در یک آرایه قرار دهیم، وضعیتهای مختلفی برای مدیریت پشتهها به شرح زیر وجود دارد:
1 top: از ابتدا تا وسط حرکت میکند.
2 top: از وسط تا انتها حرکت میکند.
| ${{\stackrel{\mathrm{top\ }\mathrm{1}\mathrm{\ \ \ }}{\longrightarrow}}}$ | ${{\stackrel{\mathrm{top\ }\mathrm{2}\mathrm{\ \ \ }}{\longrightarrow}}}$ | ||||||
| 1 | 2 | 3 | ... | n-2 | n-1 | n | |
| $\underbrace{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }_{{\mathrm{n}}/{\mathrm{2}}}$ | $\underbrace{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }_{{\mathrm{n}}/{\mathrm{2}}}$ | ||||||
1 top: از وسط تا ابتدا حرکت میکند.
2 top: از وسط تا انتها حرکت میکند.
| ${{\stackrel{\mathrm{\ \ \ \ \ \ \ \ \ \ \ top\ }\mathrm{2}\mathrm{\ \ \ \ \ \ \ \ \ \ \ }}{\longleftarrow}}}$ | ${{\stackrel{\mathrm{\ \ \ \ \ \ \ \ \ \ \ top\ }\mathrm{2}\mathrm{\ \ \ \ \ \ \ \ \ \ \ }}{\longrightarrow}}}$ | ||||||
| 1 | 2 | 3 | ... | n-2 | n-1 | n | |
| $\underbrace{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }_{{\mathrm{n}}/{\mathrm{2}}}$ | $\underbrace{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }_{{\mathrm{n}}/{\mathrm{2}}}$ | ||||||
1 top: از ابتدا تا 2 top حرکت میکند.
2 top: از انتها تا 1 top حرکت میکند
(بهترین وضعیت)
| ${{\stackrel{\mathrm{\ \ \ \ \ \ \ \ \ \ \ top\ }\mathrm{2}\mathrm{\ \ \ \ \ \ \ \ \ \ \ }}{\longleftarrow}}}$ | ${{\stackrel{\mathrm{\ \ \ \ top\ }\mathrm{2}\mathrm{\ \ \ \ }}{\longleftarrow}}}$ | ||||||
| 1 | 2 | 3 | ... | n-2 | n-1 | n | |
| $\underbrace{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }_{\mathrm{n}}$ | |||||||
در بهترین وضعیت شرایط پر شدن پشتهها به شرح زیر خواهد بود:
| ${{\stackrel{\mathrm{\ \ \ \ \ \ \ \ \ \ \ top\ }\mathrm{2}\mathrm{\ \ \ \ \ \ \ \ \ \ \ }}{\longleftarrow}}}$ | ${{\stackrel{\mathrm{\ \ \ \ top\ }\mathrm{2}\mathrm{\ \ \ \ }}{\longleftarrow}}}$ | ||||||
| 1 | 2 | 3 | ... | n-2 | n-1 | n | |
| $\underbrace{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }_{\mathrm{n}}$ | |||||||
|
وضعیت 2 top , 1 top |
شرط پر بودن پشتهها |
|
2 top, 1 top به آخرین خانه پر اشاره کنند |
$\mathrm{top\ }\mathrm{2}\mathrm{\ =\ top\ }\mathrm{1}\mathrm{\ +\ }\mathrm{1}\mathrm{\ }\mathrm{\textrm{یاا}}\mathrm{\ top\ }\mathrm{1}\mathrm{\ =\ top\ }\mathrm{2}\mathrm{-}\mathrm{1}$ |
|
2 top, 1 top یکی به آخرین خانه پر و یکی به اولین خانه خالی |
$\mathrm{top\ }\mathrm{1}\mathrm{\ =\ top\ }\mathrm{2}$ |
|
2 top, 1 top به اولین خانه خالی اشاره کنند |
$\mathrm{top\ }\mathrm{2}\mathrm{\ =\ top\ }\mathrm{1}\mathrm{\ -\ }\mathrm{1}\mathrm{\ }\mathrm{\textrm{یاا}}\mathrm{\ top\ }\mathrm{1}\mathrm{\ =\ top\ }\mathrm{2}\mathrm{+}\mathrm{1}$ |
خروجیهای مجاز برای ورودیهای پشته:
در یک پشته n تایی در صورتی که دادههای $\mathrm{a}_\mathrm{n},\ \ldots,\ \mathrm{a}_\mathrm{2},\mathrm{a}_\mathrm{1}$ به ترتیب وارد Stack شوند، با رعایت قواعد زیر میتوانیم خروجیهای مجاز را تعیین کنیم:
الف) هر داده به محض ورود میتواند از پشته خارج شود.
ب) در هر مرحله هرگاه بخواهیم دادهای را در خروجی ببینیم که هنوز وارد Stack نشده است میبایست دادهها را پشت سر هم وارد پشته کنیم تا به داده مورد نظر برسیم سپس داده را وارد پشته کرده و سپس خارج میکنیم.
ج) در هر مرحله هرگاه بخواهیم دادهای را در خروجی ببینیم که پایین Stack است و عنصر بالای پشته نیست این عمل غیرمجاز است.
مثال: یک پشته خالی با اعداد از 1 تا 6 در ورودی داده شده است. اعمال زیر بر روی پشته قابل انجام هستند:
PUSH: کوچکترین عدد ورودی را برداشته و وارد پشته میکنیم.
POP: عنصر بالای پشته را در خروجی نوشته و سپس آن را حذف میکنیم.
مثال: کدامیک از گزینههای زیر را نمیتوان با هیچ ترتیبی از ورودی فوق به دست آورد؟ (اعداد را از چپ به راست بخوانید.)(کارشناسی ارشد دولتی 74)
$\overline{\mathrm{1\ ,\ 2\ ,\ 3\ ,\ 4\ ,\ 5\ ,\ 6}}$
حل: گزینه 4 درست است.
گزینه 1 مجاز است زیرا:
6 , 5 , 4 , 3 , 2 , 1 : ورودی

4 , 6 , 5 , 3 , 2 , 1: خروجی
گزینه 2 مجاز است. زیرا:
6 , 5 , 4 , 3 , 2 , 1 : ورودی
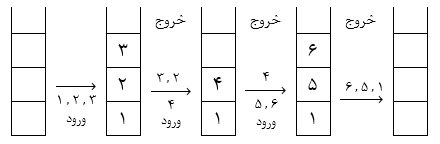
1 , 5 , 6 , 4 , 2 , 3: خروج
گزینه 3 مجاز است. زیرا:
6 , 5 , 4 , 3 , 2 , 1 : ورودی
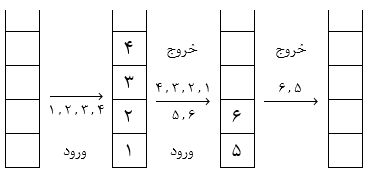
5 , 6 , 1 , 2 , 3 , 4: خروج
گزینه 4 امکانپذیر نیست، زیرا:ا:
6 , 5 , 4 , 3 , 2 , 1 : ورودی
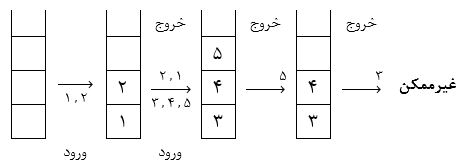
4 , 6 , 3? , 5 , 1 , 2: خروج
تعداد خروجی مجاز
تعداد خروجیهای مجاز در یک پشتهی n تایی همان عدد کاتالان بوده و به صورت زیر به دست میآید:
$\frac{\left(\begin{matrix}\mathrm{2n}\\\mathrm{n}\\\end{matrix}\right)}{\mathrm{n\ +\ 1}}$
مثال: در صورتی که$\overline{\mathrm{1,2,3}}$به ترتیب وارد یک پشته شوند تعداد حالتهای مجاز کدام هستند؟
$\mathrm{n\ =\ 3\ \rightarrow}\frac{\left(\begin{matrix}\mathrm{6}\\\mathrm{3}\\\end{matrix}\right)}{\mathrm{3\ +\ 1}}=\mathrm{5}$تعداد حالت های مجاز
خروجیهای مجاز و غیرمجاز به شرح زیر میباشد:
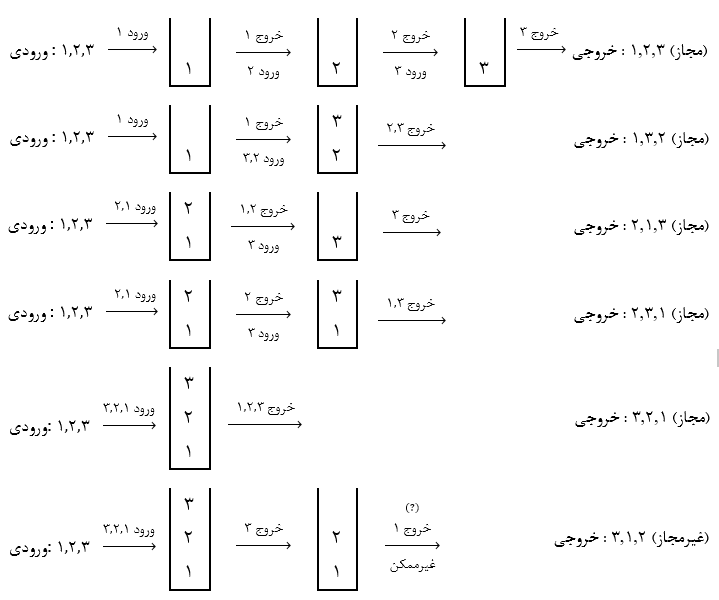
پشتههای مجاز
یک پشته از ورودی دادهها زمانی مجاز است که دادههای قبلی روی دادههای بعدی قرار نگیرند، چرا که دادههای قبلی یا باید قبلاً پشته شده و از آن خارج شده باشند یا این که خارج نشده باشند و پایین دادههای بعدی باشند.
مثال: ورودی$\overline{\mathrm{A\ ,\ B\ ,\ C\ ,\ D\ ,\ E\ ,\ F}}$به یک پشته را در نظر بگیرید، کدامیک از ترتیبهای زیر در پشته مجاز (ممکن) است؟
ابتدا B , A وارد شده سپس B خارج شده D , C وارد شده سپس D خارج شده E وارد میشود. (مجاز)
C
A
ابتدا A وارد سپس خارج شده سپس E , D , C , B وارد شده سپس C , D , E خارج شده F وارد میشود. (مجاز)
B
A یا باید پایین B قرار گیرد یا قبلاً از پشته حذف شده باشد. (غیرمجاز)
B
D
پشته چندگانه (Multiple Stack)
برای نمایش n پشته در یک آرایه m تایی مانند$\mathrm{stack}\left[\mathrm{1\ ..\ m}\right]$آرایه مورد نظر را به n قسمت مساوی تقسیم کرده و به پشته خانههای مشخص تخصیص داده میشود.
نکته: سعی داریم که فضای m خانه آرایه را بهطور مساوی بین n پشته تقسیم کنیم در این حالت اگر n مضربی از m نباشد، فضای اضافی از آرایه m تایی به پشته آخر میرسد.
مثال: 3 پشته در آرایه 10 تایی:
در این حالت برای هر پشته $\left\lfloor\frac{\mathrm{10}}{\mathrm{3}}\right\rfloor=\mathrm{3}$خانه در نظر گرفته میشود اما یک خانه اضافی به پشته آخر میرسد.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| $\underbrace{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }_{\textrm{پشته اول}}$ | $\underbrace{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }_{\textrm{پشته دوم}}$ | $\underbrace{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }_{\textrm{پشته سوم}}$ | |||||||
پیادهسازی
برای پشته i ام از دو اشارهگر$\mathrm{b}\ \left[\mathrm{i}\right]$(اشاره به ابتدای پشته) و $\mathrm{t\ }\left[\mathrm{i}\right]$(اشاره به انتهای پشته) استفاده میشود. $\mathrm{t\ }\left[\mathrm{i}\right]$به اولین خانهی خالی اشاره میکند.
شرایط مرزی
| پشته i ام پر (Full) | پشته i ام خالی (Empty) |
| $\mathrm{t\ }\left[\mathrm{i}\right]=\mathrm{b\ }\left[\mathrm{i\ +\ 1}\right]$ | $\mathrm{b\ }\left[\mathrm{i}\right]=\mathrm{t\ }\left[\mathrm{i}\right]=\left(\mathrm{i}-\mathrm{1}\right)\left\lfloor\frac{\mathrm{m}}{\mathrm{n}}\right\rfloor+\mathrm{1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i\ =\ 1\ ,\ 2\ ,\ \ldots\ ,\ n}$ |
نکته: شرایط پر بودن پشته nام :$\mathrm{t\ }\left[\mathrm{i}\right]=\mathrm{m\ +\ 1}$
مثال: میخواهیم در یک آرایه 10 تایی 3 پشته را قرار دهیم مطلوبست شرایط اولیه برای هر پشته؟
$\left.\begin{matrix}\mathrm{m\ =\ 10}\\\mathrm{n\ =\ 3\ \ \ }\\\end{matrix}\right\}\rightarrow\left\{\begin{matrix}\mathrm{i\ =\ 1\ \rightarrow\ b\ }\left[\mathrm{1}\right]=\mathrm{t\ } \left[\mathrm{1}\right]=\left(\mathrm{1}-\mathrm{1}\right)\left\lfloor\frac{\mathrm{10}}{\mathrm{3}}\right\rfloor+\ \mathrm{1\ =\ 1} \\\mathrm{i\ =\ 2\ \rightarrow\ b\ }\left[\mathrm{2}\right]=\mathrm{t\ } \left[\mathrm{2}\right]=\left(\mathrm{2}-\mathrm{1}\right)\left\lfloor\frac{\mathrm{10}}{\mathrm{3}}\right\rfloor+\ \mathrm{1\ =\ 4} \\\mathrm{i\ =\ 3\ \rightarrow\ b\ }\left[\mathrm{3}\right]=\mathrm{t\ } \left[\mathrm{3}\right]=\left(\mathrm{3}-\mathrm{1}\right)\left\lfloor\frac{\mathrm{10}}{\mathrm{3}}\right\rfloor+\ \mathrm{1\ =\ 7} \\\end{matrix}\right.$
|
$\left\lfloor\frac{\mathrm{m}}{\mathrm{n}}\right\rfloor=\left\lfloor\frac{\mathrm{10}}{\mathrm{3}}\right\rfloor=\mathrm{3}$ تعداد خانههای هر پشته |

دیده میشود که یک خانه اضافی در انتهای آرایه به stack آخر (سوم) تعلق گرفته است.
عملیات در پشته چندگانه
push (درج)
procedure push (i: Stack Number, item : data type);
begin
if t[i] = b[i + 1] \ OR \ t[i] = m + 1 \ then
write ('Full')
else begin
stack [t[i]]: = item;
t[i]: = t[i] + 1;
end;
end;
چون در ابتدا $t[i] $به خانه خالی اشاره میکند برای درج (push)، ابتدا عمل درج انجام میشود سپس $t[i]$یک واحد به بالا حرکت میکند.
pop (حذف)
procedure pop (i: Stack Number: var item : data type);
begin
if b[i] = t[i] then
write ('Empty')
else
begin
t[i]: = t[i] - 1;
item : = stack [t[i]];
end;
چون در ابتدا t[i] به خانه خالی اشاره میکند برای حذف (pop) ابتدا t[i] یک واحد به پایین حرکت میکند تا به خانه پر برسد سپس داده موردنظر حذف شده و در item قرار میگیرد.
بعضی کاربردهای پشتهها
- استفاده در توابع بازگشتی (برجهای هانوی، تابع Ackerman، دنباله Fibonachi، ...)
- ارزیابی عبارتهای محاسباتی (lirefix-liostfix-infix&nbsli;)
- الگوریتم مسیر حرکت Maze
- پیمایش عمقی درختها و گرافها
- استفاده در روشهای مرتبسازی quicksort و mergesort&nbsli;&nbsli;

































