داوطلبان به چند دلیل نیازمند پاسخنامه تشریحی سؤالات کنکور هستند: حل تست باهدف آموزش، شبیهسازی، مرور تست و…. ازاینرو دسترسی به پاسخهای تشریحی کنکورهای سالهای گذشته برای دانشجویان حیاتی است. در این مقاله به بررسی پاسخ تشریحی سؤالات کنکور ارشد کامپیوتر ۱۳۹۶ و روشهایی برای دسترسی به آن میپردازیم. در انتهای مقاله، نحوه دسترسی به پاسخ کلیدی کنکور ارشد کامپیوتر ۱۳۹۶ و دیگر کنکورها مطرح میشود.
روش های دسترسی به پاسخ تشریحی کنکور ارشد کامپیوتر ۱۳۹۶
در ادامه مقاله دو روش برای دسترسی به جواب تشریحی تستهای کنکور کامپیوتر ۱۳۹۶ بیان خواهیم کرد.
پلتفرم آزمون کنکور کامپیوتر یک خدمت از مؤسسه کنکور کامپیوتر است که دانشجویان با استفاده از آن میتوانند به جواب تشریحی تمامی تستهای کنکور دسترسی داشته باشند. علاوهبرآن از ویژگیهایی دیگری که در صفحه پلتفرم آزمون بیان شده است استفاده کنند.
روش اول: استفاده از پلتفرم آزمون کنکور کامپیوتر
در ادامه بهعنوان نمونهای از پاسخهای تشریحی پلتفرم آزمون، پاسخ تشریحی تستهای کنکور کامپیوتر ۱۳۹۶ برای درسهای هوش مصنوعیدرس هوش مصنوعی این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده، پایگاه دادهدرس پایگاه داده ⚡️ پایگاه داده کنکور ارشد کامپیوتر و آی تی
این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده، پایگاه دادهدرس پایگاه داده ⚡️ پایگاه داده کنکور ارشد کامپیوتر و آی تی این مقاله عالی توضیح داده که درس پایگاه داده چیست و چه کاربردهایی دارد و منابع و سرفصل های درس پایگاه داده در آزمون کنکور ارشد کامپیوتر و آی تی را بررسی کرده
، مدار منطقیآموزش مدار منطقی به زبان ساده - بررسی مدار منطقی و انواع آن
این مقاله عالی توضیح داده که درس پایگاه داده چیست و چه کاربردهایی دارد و منابع و سرفصل های درس پایگاه داده در آزمون کنکور ارشد کامپیوتر و آی تی را بررسی کرده
، مدار منطقیآموزش مدار منطقی به زبان ساده - بررسی مدار منطقی و انواع آن امروزه درک صحیحی از مدارهای منطقی برای هر مهندس برق و کامپیوتر ضروری است. این مدارها عنصر اصلی کامپیوترها و بسیاری از وسایل الکترونیکی اطراف ما هستند، در این صفحه به بررسی و آموزش مدار منطقی پرداخته شده است و سیگنال ها و سیستم هاهمه چیز درباره درس سیگنال و سیستم، 0 تا 100 سیگنال و سیستم
امروزه درک صحیحی از مدارهای منطقی برای هر مهندس برق و کامپیوتر ضروری است. این مدارها عنصر اصلی کامپیوترها و بسیاری از وسایل الکترونیکی اطراف ما هستند، در این صفحه به بررسی و آموزش مدار منطقی پرداخته شده است و سیگنال ها و سیستم هاهمه چیز درباره درس سیگنال و سیستم، 0 تا 100 سیگنال و سیستم این صفحه به معرفی درس سیگنال و سیستم به زبان ساده پرداخته، همچنین پیش نیاز درس سیگنال و سیستم و سرفصلهای آن بررسی و منابع درس سیگنال و سیستم معرفی شده است ارائه شده است.
این صفحه به معرفی درس سیگنال و سیستم به زبان ساده پرداخته، همچنین پیش نیاز درس سیگنال و سیستم و سرفصلهای آن بررسی و منابع درس سیگنال و سیستم معرفی شده است ارائه شده است.
تست های درس هوش مصنوعی کنکور کامپیوتر ۱۳۹۶ به همراه پاسخ نامه تشریحی
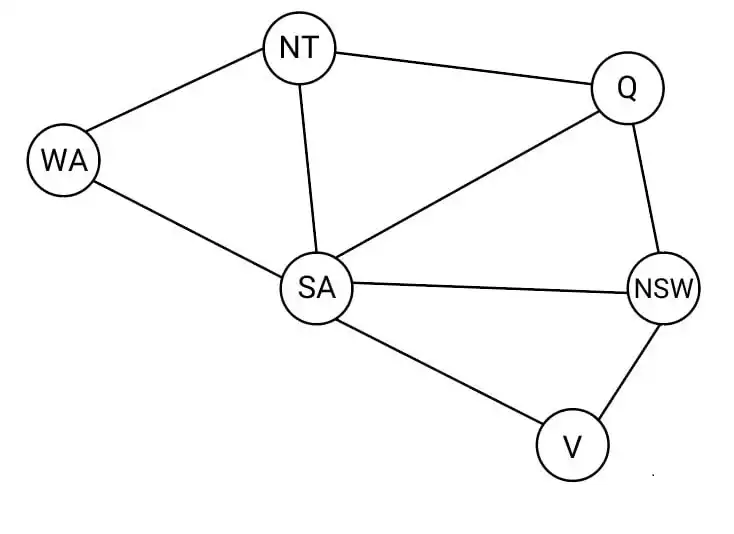
دشوار میخواهیم گراف زیر را با سه رنگ رنگآمیزی نماییم. هیچ دو رنگ مشابهی نمیتوانند کنار یکدیگر باشند. اگر مقدار NT = red و V = red باشد، آنگاه این ناسازگاری با کدامیک از روشهای زیر قابل تشخیص است؟
مسائل ارضای محدودیت
1 Forward checking
2 Arc-consistency
3 Path-consistency
4 موارد 3 و 2
گزینه 3 صحیح است.
یادآوری :
Forward checking : در این روش با هر مقداردهی با متغیرها دامنه مقادیر همه متغیرهای بدون مقدار که دارای محدودیت با متغیر مقداردهی شده میباشند بررسی و بروزرسانی میشوند. در این حالت در صورتی که به دامنه تهی برای یکی از متغیرها برسیم ناسازگاری رخ داده و عقبگرد میکنیم.
Path consistency : سازگاری مسیر به این معنی است که اگر برای دو متغیر مقدار مجاز و معتبر وجود داشته باشد برای متغیر سوم نیز حداقل یک مقدار مجاز و معتبر وجود دارد پس اگر در گراف به ازای هر سه متغیر نکته بالا برقرار باشد میتوان گفت سازگاری مسیر داریم.
Arc Consistency : همان سازگاری کمان است که در این روش با هر مقداردهی به متغیرها دامنه مقادیر همه متغیرهای بدون مقدار که دارای محدودیت با متغیر مقداردهی شده می باشند بررسی و بروزرسانی میشوند. در این حالت در صورتی که به دامنه تهی برای یکی از متغیرها برسیم ناسازگاری رخ میدهد.
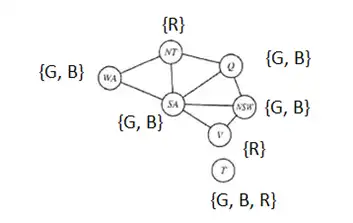
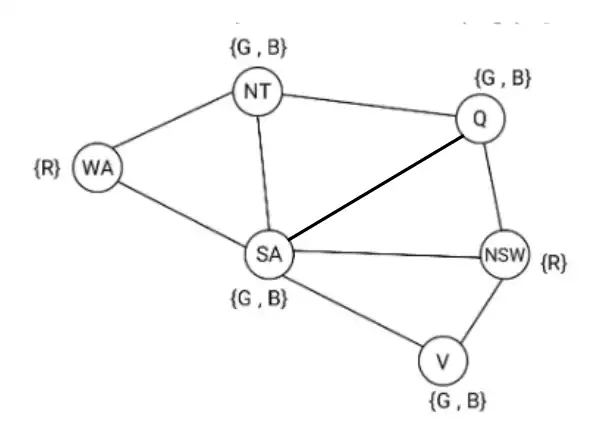
در این سوال با اعمال Forward checking میتوان به شکل بالا رسید که همانطور که مشاهده میشود دامنهی هیچ متغیر تهی نشده است .
از طرفی سازگاری کمان نیز برقرار است چرا که به ازای هر یال میتوان مقادیری را به دو سر آن با فرض اینکه محدودیتها مطابق شکل بالا هستند اختصاص داد.
اما ناسازگاری مسیر در گراف داده شده برقرار نیست چرا که به ازای سه متغیر {SA, Q, NSW} برای هر دو متغیر امکان مقداردهی معتبر وجود دارد اما امکان مقداردهی برای متغیر سوم نیست و این امر باعث ناسازگاری مسیر میشود.
توجه: در سؤال اصلی کنکور، صورت سوال NT = red و V = green است که نادرست است و هیچکدام از روشهای ذکر شده در گزینهها امکان تشخیص این ناسازگاری را ندارند زیرا با این رنگها میتوان یک ترکیب درست برای تمام متغیرها یافت، (این تست کنکور از دفترچه حذف شده است.) در اینجا (برای تمرین) فرضیات سوال را به NT = red و V = red تغییر دادهایم تا بتوان به حل سوال پرداخت.
متوسط در منطق مرتبه اول کدام عبارت «گزاره همواره درست» نیست؟ منطق مرتبه اول
1 $\left(\exists \mathrm{xP}\left(\mathrm{x}\right)\to \mathrm{Q}\right)\mathrm{\to }\left(\mathrm{\forall }\mathrm{x}\left(\mathrm{P}\left(\mathrm{x}\right)\to \mathrm{Q}\right)\right)$
2 $\left(\left(\mathrm{\neg P\ }\mathrm{\to }\mathrm{\ Q}\right)\wedge \left(\mathrm{P\ }\mathrm{\to }\mathrm{\ R}\right)\right)\mathrm{\to }\left(\mathrm{\neg P\ }\mathrm{\to }\mathrm{\ R}\right)$
3 $\left(\exists \mathrm{x}\left(P\left(\mathrm{x}\right)\rightarrow Q\left(\mathrm{x}\right)\right)\right)\leftrightarrow\left(\forall \mathrm{x} P\left(\mathrm{x}\right)\rightarrow\exists \mathrm{x} Q\left(\mathrm{x}\right)\right)$
4 گزینه 2
گزینه 2 صحیح است.
گزینه ۱ : در این گزاره اثبات میکنیم دو طرف عبارت یکی است و این نتیجهگیری برقرار است:
$\left(\mathrm{\exists }\mathrm{xP}\left(\mathrm{x}\right)\mathrm{\to }\mathrm{Q}\right)$
$\mathrm{(\neg \ }(\mathrm{\exists }\mathrm{xP}\mathrm{(}\mathrm{x}\mathrm{))}\mathrm{\vee }\mathrm{Q}\mathrm{)}$
$\mathrm{(}\mathrm{\forall }\mathrm{x\ }\mathrm{\neg }\mathrm{P}\mathrm{(}\mathrm{x}\mathrm{)}\mathrm{\vee }\mathrm{Q}\mathrm{)}$
$\mathrm{(}\mathrm{\forall }\mathrm{x\ (P}\mathrm{(}\mathrm{x}\mathrm{)}\mathrm{\to }\mathrm{Q)}\mathrm{)}$
گزینه ۲ : این گزینه همواره برقرار نیست و مثال نقض آن حالتی است که P = F و R = F و Q = T باشد.
گزینه ۳ : میتوان طبق روابط زیر اثبات کرد که رابطه دو طرفه داده شده در این گزینه درست است و دو طرف معادل هستند.
$\left(\forall xP\left(x\right)\to \exists xQ\left(x\right)\right)$
$\left(\exists x\ \neg P\left(x\right)\vee \exists xQ\left(x\right)\right)$
$\left(\exists x\ (\neg P\left(x\right)\vee Q\left(x\right))\right)$
$\left(\exists x\ (P\left(x\right)\to Q\left(x\right))\right)$
پس با توضیحات بالا گزینه دوم صحیح است.
آسان روبات برفپاککن در خودرو جزء کدام دسته از عاملهای هوشمند است؟ عامل ها و محیط ها
1 واکنشی با حافظهی داخلی
2 واکنشی ساده
3 هدفگرا
4 سودمندگرا
گزینه 2 صحیح است.
ابتدا به توضیح انواع دستههای داده شده در گزینهها میپردازیم:
واکنشی با حافظه داخلی : این عامل مشاهدات محیط را بررسی و وضعیت جاری را براساس آنها و اطلاعات موجود در حافظه داخلی مشخص میکند و این کار را با استفاده از مجموعهای از قواعد اگر و آنگاه انجام میدهد.
واکنشی ساده : این عامل مشاهدات محیط را بررسی و وضعیت جاری را براساس آنها مشخص میکند و این کار را با استفاده از مجموعهای از قواعد اگر و آنگاه انجام میدهد.
هدف گرا : این عامل براساس شواهد محیط و مجموعه حالات درونی و الگوی جهان مسئله و اهداف تعیین شده در مسئله به انتخاب کنش بعدی میپردازد.
سودمندگرا : این عامل براساس شواهد محیط و مجموعه حالات درونی و الگوی جهان مسئله و معیار سودمندی به انتخاب کنش بعدی میپردازد.
با توجه به توضیحات بالا و اینکه میدانیم در عامل برف پاک کن خودرو هیچ حافظهای نداریم این عامل جزء دسته واکنشی ساده طبقهبندی میشود.
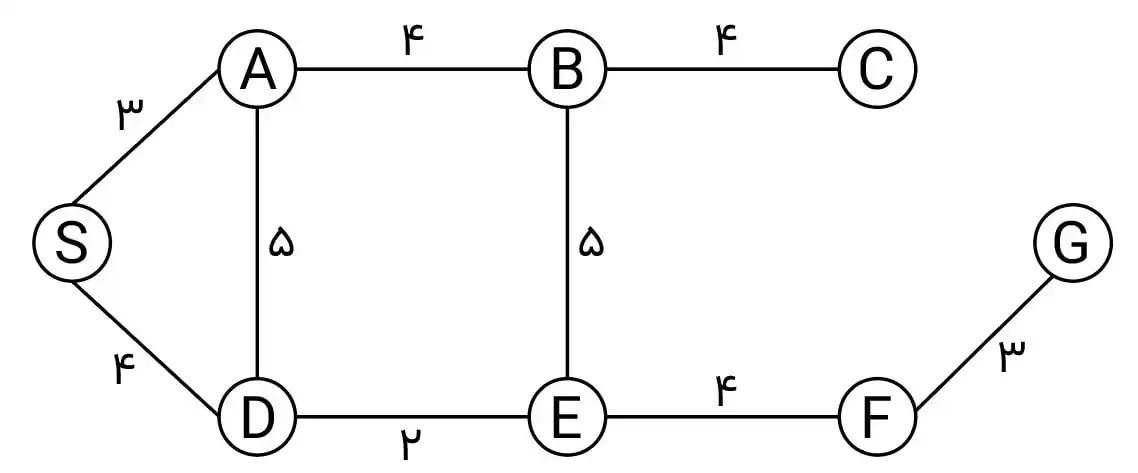
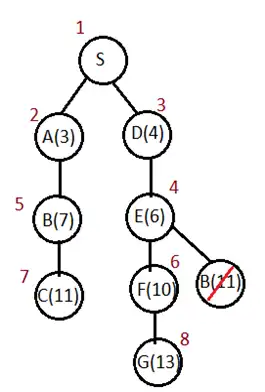
متوسط در مسألۀ زیر برای رسیدن از S به G با استفاده از روش جستجوی هزینۀ یکنواخت (uniform cost search) در حالت جستجوی گرافی، کدام گرهها به ترتیب پیمایش میشوند؟
الگوریتم های جستجوی ناآگاهانه
1 SDEFG
2 SADEFG
3 SADEBFG
4 SADEBFCG
گزینه 4 صحیح است.
درخت حاصل از اجرای الگوریتم UCS و ترتیب گسترش گرهها
دشوار اگر KB یک پایگاه دانش بهصورت منطق گزارهای باشد، کدام جمله نادرست است؟ منطق گزارهای
1 اگر $\mathrm{\alpha }\mathrm{\ }\mathrm{\models }\mathrm{\ }\mathrm{\beta}\mathrm{\ }$ آنگاه $\mathrm{\neg }\mathrm{\beta }\mathrm{\ }\mathrm{\models }\mathrm{\ \neg }\mathrm{\alpha }$
2 اگر $\mathrm{KB\ }\mathrm{\models }\mathrm{\ }\mathrm{\alpha }$ ممکن است $\mathrm{KB\ }\mathrm{\wedge }\mathrm{\ B\ }\mathrm{\nvDash }\mathrm{\ }\mathrm{\alpha }\mathrm{\ }$
3 ممکن است يک جملهی $\alpha$ وجود داشته باشدکه $\mathrm{KB\ }\mathrm{\nvDash }\mathrm{\ }\mathrm{\alpha }$ و $\mathrm{KB\ }\mathrm{\nvDash }\mathrm{\ \neg }\mathrm{\alpha }$
4 اگر در همهی وضعيتهايی که KB صحيح است $\alpha$ هم صحيح باشد آنگاه $\mathrm{KB\ }\mathrm{\models }\mathrm{\ }\mathrm{\alpha }$
گزینه 2 صحیح است.
گزینه ۱ : عبارت این سوال قاعده نقیض را بیان میکند و میتوان آن را با استفاده از تبدیل گزاره به قواعد جبری نیز اثبات کرد. میدانیم که $\alpha \models \beta $ معادل است با $\neg \alpha \vee \beta $. با استفاده از این تعریف هر دو عبارت $\alpha \models \beta $ و $\neg \beta \models \neg \alpha$ معادل $\neg \alpha \vee \beta $ میباشند پس قابل نتیجهگیری از روی یکدیگر هستند.
گزینه ۲ : اگر پایگاه دانش خاصیت یکنوایی داشته باشد با اضافه شدن حقیقت جدید به آن (B) نباید نتیجهگیریها و قواعد قبلی نقض شود پس اگر بدانیم $KB \models \alpha $ برقرار بوده است، با اضافه شدن حقیقت B باز هم باید $KB \wedge B \models \alpha$ برقرار باشد و این گزینه نادرست است.
گزینه ۳ : وقتی میگوییم $KB \models \alpha $ که $M(KB) \subseteq M(\alpha)$ باشد با این تعریف در حالتی که $\alpha$ بخشی از KB را شامل شود $\mathrm{KB}~\mathrm{\nvDash }~\alpha \mathrm{\ }و\mathrm{\ }\mathrm{KB}~\mathrm{\nvDash }~\mathrm{\neg }\alpha $ رخ میدهد.
گزینه ۴ : وقتی میگوییم $KB \models \alpha $ که $M(KB) \subseteq M(\alpha)$ باشد و اگر در همهی وضعيتهايی که KB صحيح است α هم صحيح باشد آنگاه میتوان گفت $M(KB) \subseteq M(\alpha)$ برقرار میباشد و در این حالت میتوان $KB \models \alpha $ را نتیجه گرفت.
دشوار در مورد بازی دو نفره صفر جمع (Zero - Sum) اگر بخواهیم از الگوریتم Minimax استفاده کنیم تا حرکت بهینه را برای بازیکن مورد نظر پیدا کنیم، کدام مورد درست نیست؟ بازی های رقابتی
1 چنانچه سودمندی (utility) وضعیتهای پایانی بازی را در یک عدد مثبت ضرب نموده و با یک عدد ثابت جمع کنیم تأثیری در حرکت بهینه پیدا شده توسط minimax ندارد.
2 اگر بازیکن حریف بهینه عمل نکند لزوماً الگوریتم minimax منجر به حداکثر کردن سودمندی (utility) برای بازیکن مورد نظر نمیشود.
3 الگوریتم هرس β - α تأثیری در کیفیت جواب به دست آمده توسط روش minimax ندارد و فقط زمان را کاهش میدهد.
4 سودمندی (utility) که برای بازیکن مورد نظر با استفاده از این روش در مقابل حریف غیربهینه به دست میآید، ممکن است کمتر از سودمندی (utility) به دست آمده در مقابل حریف بهینه باشد.
گزینه 4 صحیح است.
گزینه ۱ : درست است چرا که در این صورت ترتیب و بزرگ یا کوچکتر بودن سودمندی گرهها نسبت به یکدیگر تغییری نمیکند.
گزینه ۲ : این گزینه نیز درست است چرا که بطور کلی روش جستجو minimax به دنبال حداکثر کردن حداقل سودمندی است و این حداقل سودمندی زمانی که بازیکن حریف بهینه عمل کند حاصل میشود.
گزینه ۳ : این گزینه نیز درست است.
گزینه ۴ : این گزینه نادرست است چرا که بطور کلی روش جستجو minimax به دنبال حداکثر کردن حداقل سودمندی است و امکان ندارد در مقابل هیچ حریفی (مثلا حریف غیر بهینه) سودمندی کمتر از سودمندی بدست آمده در مقابل حریف بهینه بدست آید.
آسان در جستجوی درختی (Tree-Search) با استفاده از روشهای جستجوی ناآگاهانه (Uniformed) کدام مورد درست نیست؟ الگوریتم های جستجوی ناآگاهانه
1 حافظۀ لازم برای IDS برحسب عمق، کم عمقترین گره هدف خطی است.
2 حافظۀ لازم برای BFS برحسب عمق، کم عمقترین گره هدف نمایی است.
3 حافظۀ لازم برای DFS برحسب عمق، کم عمقترین گره هدف همیشه خطی است.
4 حافظۀ لازم برای جستجوی دوجهتی (Bidirectional) برحسب عمق، کم عمقترین گره هدف نمایی است.
بررسی گزینهها:
گزینه ۱:
الگوریتم IDS (Iterative Deepening Search) در هر مرحله تا یک لول مشخص جستوجوی DFS انجام میدهد و در مرحله بعدی یک سطح جلوتر میرود.
این الگوریتم بهینه بوده و نزدیکترین گره به ریشه پیدا میکند.
بیشترین حافظه لازم برابر عمقی است که برای یافتن بهینهترین هدف (کم عمقترین هدف) طی میکند و از مرتبه $O(bd)$ است.
این گزینه صحیح است.
گزینه ۲:
الگوریتم BFS بهینه عمل میکند و همیشه کم عمقترین هدف را پیدا میکند.
حافظه لازم در هر عمقی که BFS در حال جستوجوی آن است از مرتبه $O(b^d)$ است که d عمق گره هدف بهینه (کم عمقترین هدف) میباشد و b متوسط فرزندان هر گره (فاکتور انشعاب) است.
بنابراین بیشترین حافظهای که BFS نیاز دارد نیز از این مرتبه است و همانطور که مشخص است این مرتبه نمایی است.
این گزینه نیز صحیح میباشد.
گزینه ۳:
مرتبه حافظه مورد نیاز در DFS، بر حسب عمقی که در آن در حال جستوجو است خطی است و بطورکلی مرتبه حافظه DFS از مرتبه $O(bm)$ است که m بیشترین عمق در درخت است، پس حافظه DFS بر حسب m خطی است نه بر حسب b. توجه کنید که این الگوریتم تضمین نمیکند که همیشه بهینهترین هدف (کم عمقترین هدف) را اول بیابد.
این گزینه غلط است و جواب این گزینه است.
گزینه ۴:
جستوجوی bidirectional از لحاظ حافظه مشابه BFS عمل میکند. این گزینه نیز صحیح است.
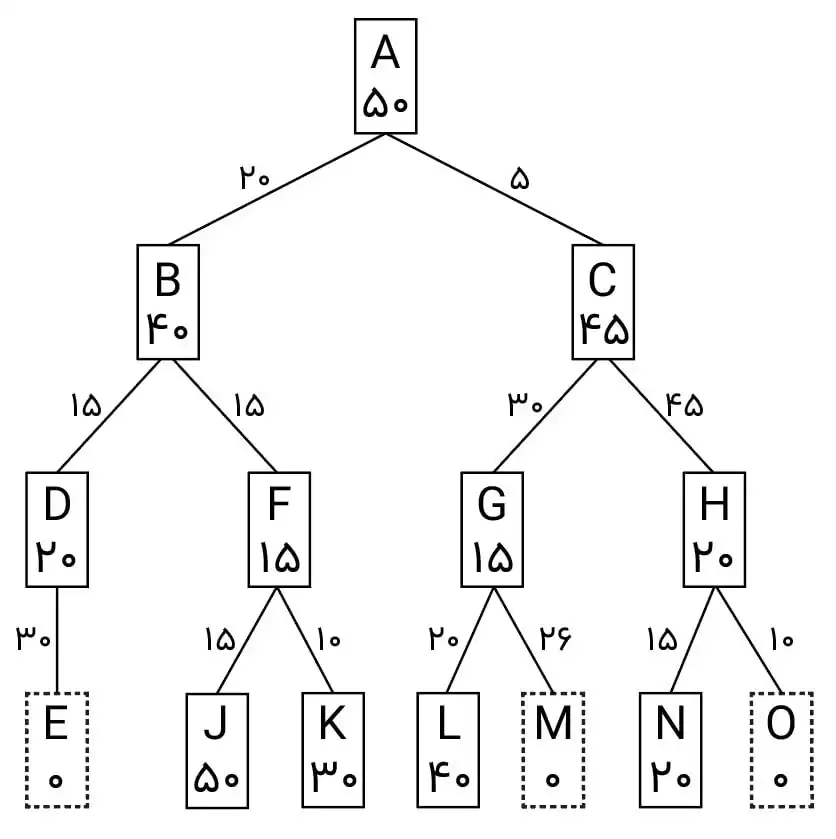
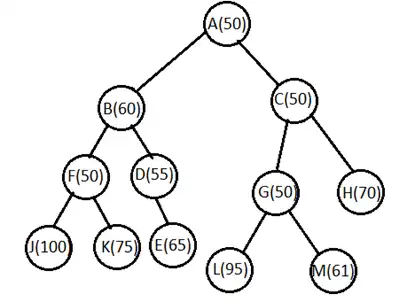
دشوار درخت جستجوی زیر داده شده است. گره A، وضعیت اولیه میباشد. وضعیتهای جواب نیز با مربعهای نقطهچین نشان شدهاند. اعداد روی یالها هزینه استفاده از آن مسیر (یال) را نشان میدهد. اعداد داخل هر گره نیز تخمین فاصله تا هدف را مشخص میکند. اگر برای جستجو از روش \( {IDA}^* \) استفاده شود، میزان حد آستانه که جهت انتخاب گرهها، هنگام ورود به صف در نظر گرفته میشود پس از گرفتن مقدار اولیه، چندبار
تغییر میکند؟
الگوریتم های جستجوی آگاهانه
1 0
2 1
3 2
4 3
گزینه 3 صحیح است.
یادآوری روش IDA* و نکات مربوط به آن :
روش IDA* روشی مشابه A* است که در جهت بهبود وضعیت مرتبه حافظه A* ارائه شده است و از ایده جستجو عمقی تکرار شونده استفاده میکند. پس مصرف حافظه این روش نسبتا خوب است و از آنجا که برمبنای A* و جستجو عمقی تکرار شونده است کامل نیز میباشد و کارایی خوبی دارد چرا که مرتبه زمانی آن مشابه A* است. در این روش درخت جستجو به صورت تکراری از ریشه تا زمانی که مقدار تمام گره ها از cutoff بیشتر شود به صورت عمقی ساخته میشود (به عبارتی همه گره هایی که f(n) آنها از cutoff کمتر است به صورت پیش ترتیب بررسی میشوند). سپس در هر تکرار مقدار cutoff به کوچکترین مقدار f(n) گره های موجود در گراف بروزرسانی میشود تا جایی که به هدف برسیم. این روش از آنجا که در هر مرحله کل درخت جستجو از ابتدا میسازد، دوباره کاری دارد که یکی از نقطه ضعف های آن محسوب میشود.
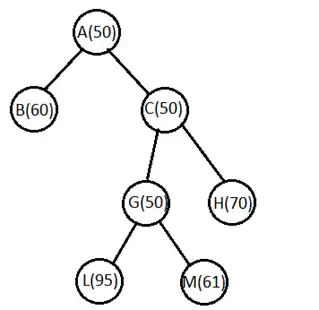
در مرحله اول cutoff = 50 در نظر گرفته میشود و درخت زیر بدست میآید:
در مرحله بعدی cutoff به کمترین مقدار f(n) یعنی ۶۰ تنظیم میشود :
از آنجایی که هنوز به هدف نرسیدم بازهم الگوریتم را ادامه میدهیم و در مرحله بعدی cutoff به کمترین مقدار f(n) یعنی ۶۱ تنظیم میشود و در این مرحله گره M بسط داده شده و به هدف میرسیم. پس به جز تنظیم اولیه cutoff به مقدار 50 ، دوبار مقدار cutoff تغییر کرد و جواب گزینه سوم میباشد.
دشوار با درنظر گرفتن الگوریتم جستجوی بهترین حریصانه (GBFS)، \( {A}^* \) و الگوریتمهای مشتقشده از آن: \( {IDA}^* \) و \( {SMA}^* \) چند مورد از گزینههای زیر درست است؟
الگوریتم های جستجوی آگاهانه
الف) الگوریتم \( {A}^* \) همان GBFS است که ملاک انتخاب گره بعدی آن، به جای «نزدیکتر بودن فاصله تا هدف»، «کمینه بودن مجموع هزینه رسیدن به گره حاضر و هزینه رفتن از گره حاضر به هدف» میباشد.
ب) \( {A}^* \) گرههایی با تخمین هزینهای کمتر از هزینه واقعی را نادیده گرفته و هرس میکند.
ج) \( {IDA}^* \) با الهام گرفتن از ایدهی عمیقکننده تکراری روی الگوریتم \( {A}^* \) کار میکند و هدف آن کاهش مشکل اصلی \( {A}^* \) یعنی پیچیدگی زمان توانی است.
د) \( {SMA}^* \) با الهام گرفتن از ایدهی «الگوریتم بهترین جستجوی بازگشتی» روی \( {A}^* \) کار میکند و در صورتی که عمق سطحیترین گره هدف کمتر از حافظه تخصیصی باشد کامل خواهد بود و اگر هدفی در دسترس باشد بهینه است.
1 0
2 1
3 2
4 4
گزینه 3 صحیح است.
الف ) این گزاره درست است چرا که در روش جستجو GBFS در واقع f(n) = h(n) میباشد در حالی که در A* داریم f(n) = h(n) + g(n) .
ب) در واقع اگر منظور از هزینه واقعی، هزینه بهینه رسیدن گره ابتدایی به هدف باشد، در این الگوریتم گرههایی که هزینه کمتر از این مقدار برای رسیدن به هدف دارند بسط داده میشوند و این گزینه نادرست است.
ج) IDA* با الهام گرفتن از ایدهی عمیقکننده تکراری روی الگوریتم A* کار میکند و هدف آن کاهش مشکل اصلی A* یعنی پیچیدگی حافظه توانی است. بنابراین گزاره ج نادرست است.
د) این گزاره را میتوان درست در نظر گرفت اما شکل صحیح تر آن به صورت زیر است :
SMA* با الهام گرفتن از ایدهی «الگوریتم بهترین جستجوی بازگشتی» روی A* کار میکند و در صورتی که عمق سطحیترین گره هدف کمتر از حافظه تخصیصی باشد کامل خواهد بود و اگر با حافظه تخصیصی امکان رسیدن به هدف بهینه وجود داشته باشد آن را بعنوان هدف برمیگرداند و در غیر اینصورت بهینهترین هدف با توجه به حافظه تخصیصی را برمیگرداند (یعنی ممکن است نسبت به مسیری که برمیگرداند، مسیر دیگری که بهینهتر است اما حافظه مورد نیاز برای رسیدن به آن بیشتر است وجود داشته باشد)
با توجه به توضیحات بالا فقط گزارههای الف و د صحیح هستند.
دشوار مسأله 8-puzzle را درنظر بگیرید. یک database داریم که به ازای هر ترکیب چهارتایی از اعداد 1- 8، میانگین حل مسأله صرفاً آن چهار عدد تا جواب، در آن ذخیره شده است. به عنوان مثال c(1,2,3,4) تعداد جابهجایی مورد نیاز جهت جابهجا کردن صرفاً اعداد 1 و 2 و 3 و 4 تا محلهای جواب است. آنگاه بهترین تابع admissible از بین گزینهها کدام است؟ الگوریتم های جستجوی آگاهانه
1 \(\mathrm{H(n)\ =\ }\frac{\left(\mathrm{c\ }\left(\mathrm{1}\mathrm{,\ }\mathrm{2}\mathrm{,\ }\mathrm{3}\mathrm{,\ }\mathrm{4}\right)\ +\mathrm{\ c}\left(\mathrm{5}\mathrm{,\ }\mathrm{6}\mathrm{,\ }\mathrm{7}\mathrm{,\ }\mathrm{8}\right)\right)}{\mathrm{2}}\)
2 \(\mathrm{H(n)\ =\ min}\left(\mathrm{c}\left(\mathrm{1}\mathrm{,\ }\mathrm{2}\mathrm{,\ }\mathrm{3}\mathrm{,\ }\mathrm{4}\right),\mathrm{c}\left(\mathrm{1}\mathrm{,\ }\mathrm{3}\mathrm{,\ }\mathrm{5}\mathrm{,\ }\mathrm{7}\right)\right)\)
3 \(\mathrm{H(n)\ =\ sqrt}\left(\mathrm{c}\left(\mathrm{1}\mathrm{,\ }\mathrm{2}\mathrm{,\ }\mathrm{3}\mathrm{,\ }\mathrm{4}\right)\ +\ \mathrm{c}\left(\mathrm{5}\mathrm{,\ }\mathrm{6}\mathrm{,\ }\mathrm{7}\mathrm{,\ }\mathrm{8}\right)\right)\)
4 نمیتوان به قطعیت گفت کدام تابع بهتر است.
گزینه 1 صحیح است.
در این سوال توابع داده شده در گزینه ۱ تا ۳ همگی قابل قبول هستند و ترتیب آنها به صورت زیر است:
$h_2 \lt h_3 \lt h_1 \lt h^*$
تابع داده شده در گزینه اول به میانگین حسابی اشاره میکند که یکی از توابع هیوریستیک قابل قبول و میدانیم که از min و جذر مجموع هیوریستیکها دقیق تر است. گزینه دوم فقط کمینه یکی از حالات را در نظر میگیرد در نتیجه نسبت به سایر توابع چندان مناسب نیست. تابع گزینه سوم نیز قابل قبول است اما اگر از حاصلضرب هزینهها جذر گرفته میشد (معادل میانگین هندسی) بهتر بود و تابع دقیقتری بدست میآمد اما باز هم این تابع از تابع گزینه دوم بهتر است.
دشوار مسأله رنگآمیزی زیر با سه رنگ را درنظر بگیرید و فرض کنید که مقدار رنگ WA و NSW هر دو قرمز است. بهترین روشی که میتوان این ناسازگاری را پیدا کرد، کدام مورد است؟
مسائل ارضای محدودیت
1 Arc Consistency
2 All Diff Heuristic
3 Forward Checking
4 Resource Constraint Heuristic
گزینه 2 صحیح است.
با توجه به شکل زیر برای پیدا کردن ناسازگاری که بین سه گره Q, SA, NT وجود دارد نمیتوان از Arc Consistency و Forward Checking استفاده کرد.
Resource Constraint Heuristic:
یکی از انواع محدودیتهای عمومی است که دارای دو قاعده مهم است :
1- مجموع حداقل دامنه متغیرها باید در قید برقرار باشد.
2- اگر حداکثر مقدار یک متغیر با حداقل مقدار سایر متغیرها ناسازگار باشد آنگاه مقدار حداکثر باید از دامنه حذف شود.
این هیوریستیک متناظر با محدودیتهایی است که حداکثر و حداقل مقادیر را برای متغیرها تعیین میکنند و مرتبط با این سوال نیست.
All Diff Heuristic:
این محدودیت به بررسی تمایز مقادیر مجموعهای از متغیرها میپردازد که ناسازگاری موجود در این سوال را میتوان به وسیله این محدودیت و با تعریف این محدودیت روی مثلث {NT, Q, SA} کشف کرد.
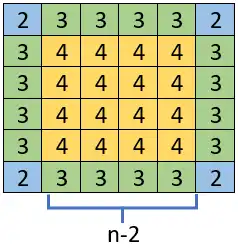
دشوار مسأله Wampus World که در یک فضای شطرنجی n*n است در نظر بگیرید که در آن عامل A و دو هیولا H1, H2 وجود دارد و هدف آن است که عامل بدون برخورد به هیولا از خانه (1,1) به خانه (n,n) برود. اگر بخواهیم مسأله را با منطق گزارهها حل کنیم، به چند جمله نیاز داریم؟
منطق گزارهای
(فرض کنید که عامل یکی از چهار عمل Left/Right/Up/Down را میتواند انجام دهد که حرکت در چهار جهت است. هیولاها نیز ثابت هستند و حرکت نمیکنند.)
1 جمله $N^2$
2 $(n – 1)^2 + (n – 1) + 8$
3 $4(n – 2)^2 +12(n – 2)+ 8$
4 این مسأله با منطق گزارهها قابل مدلسازی نیست.
باید برای هر خانه ای بنویسیم که عامل چه حرکاتی برایش مجاز است.
مثلا اگر عامل در خانه (1,1) است اگر حرکت right را انجام بدهد به خانه (2,1) میرود و اگر حرکت up را انجام بدهد به خانه (1,2) میرود، پس برای خانه (1,1) باید 2 جمله با منطق گزارهای بنویسیم.بنابراین تعداد قوانینی که نیاز است برای هر خانه نوشته شود برابر تعداد خانههای مجاور آن خانه است.
چون گزینهها به صورت پارامتری است میتوان با گذاشتن مقدار به جای n و رد گزینه به جواب صحیح برسیم.
برای n=2 طبق شکل زیر تعداد جملات برابر 8 است.
1)$ 2^2=4$
2)$ (2-1)^2+(2-1)+8=10$
3)$ 4(2-2)^2+12(2-2)+8=8$
مشخص است که فقط گزینه 3 به ازای n=2 برابر 8 میشود و جواب سوال میشود.اگر با n=2 دو یا چند گزینه برابر 8 میشد،میتوانستیم با گزاشتن عدد دیگری مثلا n=3 جواب سوال را بیابیم که در این سوال نیازی به اینکار نیست.
راه حل سیستماتیک:
هر مربعی 4 خانه گوشه دارد که هرکدام نیاز به 2 جمله دارد،خانه هایی که مجاور ضلع های مربع هستند هر کدام نیاز به 3 جمله دارند و خانه های وسط هرکدام به 4 جمله نیاز دارند.
4 ×2+(n-2)×3×4+(n-2)×(n-2)×4
دشوار کدام عبارت میتواند بهطور دقیق بیانگر جمله زیر باشد؟
منطق گزارهای
(یک انسانی که خوب است (R)، انتخابشدنی است (E)، اگر خوشبین باشد (C)، در غیر این صورت انتخابشدنی نیست.)
1 $(R \land E) \Leftrightarrow C$
2 $R \Rightarrow (E \Leftrightarrow C)$
3 $R \Rightarrow((C \Rightarrow E)\vee \lnot E)$
4 هیچکدام
گزینه 2 صحیح است.
بخش دوم گزاره داده شده که میگویید «انتخاب شدنی است اگر خوشبین باشد و در غیر اینصورت انتخاب شدنی نیست» به یک رابطه دو طرفه اشاره میکند که میتوان آن را به صورت $E \Leftrightarrow C$ نوشت. از طرفی گزاره میگوید اگر یک انسانی خوب باشد این رابطه دو طرفه برقرار است یعنی $R \Rightarrow (E \Leftrightarrow C)$ که مطابق گزینه دوم است.
دشوار مسند ${P}\left(\mathrm{g}\left(\mathrm{X}\right),\mathrm{\ f}\left(\mathrm{Y\ ,\ X}\right)\right)$، با کدامیک از مسندات زیر قابل یکسانسازی (unification) هستند؟ منطق مرتبه اول
1 $\mathrm{P}\left(\mathrm{g}\left(\mathrm{Z}\right),\mathrm{\ f}\left(\mathrm{Z\ ,\ Z}\right)\right)$
2 $P(X , Y)$
3 $P(Y , X)$
4 همه موارد
گزینه 4 صحیح است.
گزینه ۱ : در صورتی که X/Z و Y/Z در نظر گرفته شود عبارت این گزینه و عبارت صورت سوال قابل یکسانسازی هستند.
گزینه ۲ : برای یکسانسازی عبارت این گزینه با عبارت صورت سوال نیاز به تغییر متغیر داریم. پس از تغییر متغیر میتوان دو عبارت را با در نظر گرفتن Z/g(X) و W/f(Y,X) یکسانسازی کرد.
$P(g(X), f(Y,X))$
$P(Z, W)$
گزینه ۳ : مشابه بالا این گزینه نیز با تغییر متغیر قابل یکسانسازی است.
پس تمامی موارد قابل یکسانسازی هستند و گزینه ۴ صحیح است.
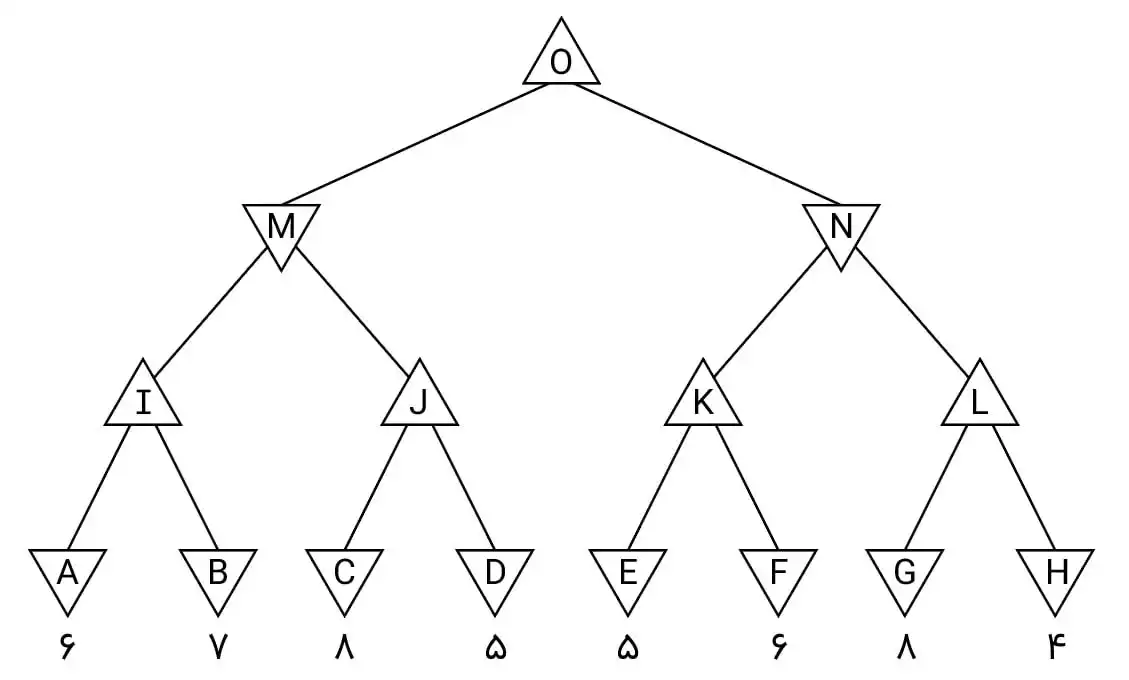
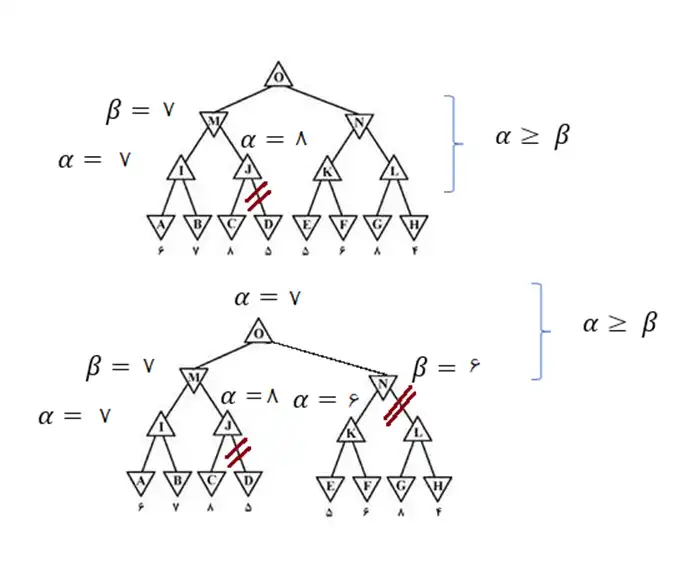
آسان اگر از روش هرس α - β استفاده شود، کدام گرههای درخت نشان داده شده جستجو
نمیشوند؟
بازی های رقابتی
1 J, C, D, L, G, H
2 D, L, G, H
3 D, F, H
4 D, F
گزینه 2 صحیح است.
برای اجرای روش هرس آلفا-بتا ابتدا از زیر درخت سمت چپ شروع میکنیم و پس از تنظیم آلفا برای گره l و بتا برای گره M به زیردرخت سمت دیگر میرویم. در مرحله بعد، پس از بررسی گره C مقدار آلفا برای گره J برابر با ۸ میشود و شرط هرس برقرار شده و گره D هرس میشود. در مرحله بعدی مقدار آلفا متناظر با ریشه تنظیم میشود و پس از بررسی گره های F و E مقدار آلفا و بتا برای به ترتیب گرههای k و N برابر با ۶ میشود. در این مرحله نیز شرط هرس مطابق شکل دوم برقرار شده است و زیردرخت نشان داده شده در شکل زیر هرس میشود.
تست های درس پایگاه داده کنکور کامپیوتر ۱۳۹۶ به همراه پاسخ نامه تشریحی
دشوار
سه رابطه قایق، قایقران و رزرو را در نظر بگیرید. میخواهیم نام قایقرانهایی را بیابیم که همه قایقها را رزرو کردهاند. کدام مورد، دستور SQL درست برای این درخواست است؟
زبان و پرس و جوی SQL
قایقران: Sailors (sid , sname)
رزرو: Reservation (sid , bid , day)
قایق: Boats (bid , bname , color)
1
Select sname from Sailors S where not exists
((Select bid from Boats B) except
(Select bid from Reservation R where R.bid = B.bid AND R.sid = S.sid))
2
Select sname from Sailors S where exists
((Select bid from Boats B) except
(Select bid from Reservation R where R.bid = B.bid AND R.sid = S.sid))
3
Select sname from Sailors S where Not exists
(Select bid from Boats B where not exists
(Select * from Reservation R where R.bid = B.bid AND R.sid = S.sid))
4
Select sname from Soulors S where exists
(Select bid from Boats B where exists
(Select * from Reservation R where R.bid = B.bid AND R.sid = S.sid))
گزینه 3 صحیح است.
قبل از حل این سوال به نکته مهم زیر توجه کنید:
| Not exist |
exist |
|
|
عدم وجود حداقل یک ارتباط
جمله منفی است.
معنی تقسیم و تفاضل میدهد.
|
وجود حداقل یک ارتباط
جمله مثبت است.
معادل با:
Join -
- In (به صورت تودر تو یا تکی)
=any -
=sum -
|
exist |
|
معنی وجود همه ارتباطات
جمله مثبت است.
معنی تقسیم میدهد.
معادل با:
=all -
not exist except -
|
وجود هیچ ارتباط
جمله منفی است.
معنای تفاضل میدهد.
معادل با:
Minus -
not in -
not exist -
(نامساوی all) !=all -
|
Not exist |
از صورت سوال متوجه میشویم که باید عمل تقسیم انجام شود.
الگوی تقسیم در Sql یا حساب رابطهای "not exist …. Not exist" و یا "not exist ….. except " است. (طبق جدول بالا) بنابراین گزینههای 2 و 4 رد میشوند.
علت رد گزینه 1: این گزینه در بخش R.bid=B.bid اشکال دارد زیرا در سمت راست تفاضل که زیر پرسوجویی مستقل است جدول B تعریف نشده و یک شرط زائد به حساب میآید. اگر این بخش حذف میشد این گزینه درست بود.
گزینه 3 درست ترین جواب برای این سوال است.
متوسط
رابطه $R(A,B,C,D,E)$ و مجموعه وابستگیهای تابعی، $F = \{(A,B) \to C , B \to D , (D , E) \to C\}$ را در نظر بگیرید. کلید کاندید این رابطه کدام است؟
طراحی پایگاه داده
1 $\{A,B,D\}$
2 $\{A,B,E\}$
3 $\{A,B,C,E\}$
4 $\{A,B,D,E\}$
گزینه 2 صحیح است.
چند نکته در رابطه با تشخیص کلید کاندید از روی مجموعه وابستگی:
1- ابتدا وابستگیهای بازتابی حذف شوند.
2- صفتی که در سمت راست هیچ وابستگی تابعی نباشد حتما در کلید است.
3- اجزا کلید به یکدیگر وابستگی تابعی ندارند.
4- صفتی که فقط در سمت راست وابستگی تابعی باشد هرگز در کلید نیست
5- اگر با این نکات کلید یافت نشد آنگاه مجموعه بسط دترمینانها محاسبه میشود و دترمینانی که کمینه باشد و همه صفات را پوشش دهد کلید کاندید است.
*بهتر است برای بررسی راحتتر، وابستگیها را زیر هم بنویسید.
$AB\to C$
$B\to D$
$DE\to C$
صفات A, B, E در سمت راست هیچیک از وابستگیها نیامدهاند بنابراین جزئی از کلید هستند.
بسط دترمینان:
$\{ABE\}+ = \{A,B,C,D,E\}$
ترکیب 3 صفت A,B,E تمامی صفات را میدهند و کمینهاند. بنابراین ABE کلید کاندید است.
متوسط
عبارت جبر رابطهی «عنوان کتابهایی از انتشارات wiley که توسط هیچ عضوی امانت گرفته
نشده» معادل کدام است؟
پایگاه داده رابطهای
Book(ISBN, Title, Author, Publisher) : کتابها
Member (MID, Name, MDate) : اعضاء
Borrow (MID, ISBN, BDate, Duration) : امانت کتاب
1 $\Pi_{ \lt Title \gt }\left(\sigma_{publisher=\prime w i l e y\prime}\left(Book\right)\right)-\Pi_{ \lt ISBN \gt }(Borrow)$
2 $\Pi_{ \lt Title ,ISBN \gt }\left(\sigma_{publisher=\prime w i l e y\prime}\left(Book\right)\right)\div\Pi_{ \lt ISBN \gt }(Borrow)$
3 $\Pi_{ \lt Title \gt }((\Pi_{ \lt ISBN.MID \gt }\left(Borrow\right)\div\Pi_{ \lt MID \gt }\left(Member\right))\bowtie Borrow)$
4 $\Pi_{ \lt Title \gt }\left(\left(\Pi_{ \lt ISBN \gt }\left(\sigma_{publisher=^\prime w i l e y^\prime}.\left(Book\right)\right)-\Pi_{ \lt ISBN \gt }\left(Borrow\right)\right)\bowtie B o o k\right)$
گزینه 4 صحیح است.
برای بهدست آوردن خروجی مورد نظر باید کل کتابهای منتشر شده توسط انتشارات wiley را منهای کلیه کتابهایی کنیم که تا کنون به امانت گرفته شدهاند. باید توجه شود که شرایط سازگاری در اجرای عملگر تفریق نقض نشود.
علت رد گزینه 1: شرط سازگاری نقض شده است.
علت رد گزینه 2 و 3: تفریق مورد نظر انجام نشده است.
در این پرسش چون عنوان کتابها خواسته شده است در گزینه 4 پس از بهدست آمدن ISBN کتابهای مورد نظر، برای بهدست آوردن عنوان کتاب، نتیجه حاصل با جدول book الحاق طبیعی شده است.
آسان
کدام مورد، عبارت حساب رابطهای معادل «نام دانشجویانی که تمام دروس 4 واحدی را اخذ کردهاند» است؟
پایگاه داده رابطهای
ST (STID ,STName ,…) دانشجویان
CO (COID, COName, Credit ,…) دروس
STCO(STID,COID, Semester, Grade) دروس انتخاب شده توسط دانشجویان
Rangevar STX Over ST
Rangevar COX Over CO
Rangevar STCOX Over STCO
1 STX.STName Where Forall COX (COX.Credit = 4 AND Exists STCOX (STCOX.STID=STX.STID AND STCOX.COID=COX.COID))
2 STX.STName Where Forall COX (COX.Credit != 4 OR NOT Exists STCOX (STCOX.STID=STX.STID AND STCOX.COID=COX.COID))
3 STX.STName Where Not Exists COX (COX.Credit = 4 AND NOT Exists STCOX (STCOX.STID=STX.STID AND STCOX.COID=COX.COID))
4 STX.STName Where Exists STCOX (STCOX.STID =STX.STID AND Exists COX (COX.COID=STCOX.COID AND COX.Credit=4))
گزینه 3 صحیح است.
از صورت سوال متوجه میشویم که باید عمل تقسیم انجام شود. الگوی تقسیم در حساب رابطهای "not exist …. Not exist" است.این الگو فقط در گزینه 3 رعایت شده است.
دشوار
فرض کنید که دید $V_1$ بر روی جداول S و SP به صورت زیر تعریف شده باشد.
زبان و پرس و جوی SQL
S (SID, SName, Level, City) Create View V1
P (PID, PName, Weight) As Select SID as ID , Sum (QTY) as SQTY
SP (SID, PID, QTY) From SP join S
Where Level >10
Group By SID
دستور زیر در سطح خارجی با نگاشت E/C تبدیل به چه دستوری در سطح ادراکی میشود؟
Select ID, SQTY
From VI
Where SQTY > 1000
1 Select ID , SQTY
From SP Join S where Level $\gt$ 10
GroupBy SID Having SQTY $\gt$ 1000
2 Select ID , SQTY
From SP Join S where Level $\gt$ 10 AND SQTY $\gt$ 1000
GroupBy ID
3 Select SID as ID , Sum (QTY) as SQTY
From SP Join S where Level $\gt$ 10
Group By SID Having Sum (QTY) $\gt$ 1000
4 Select SID as ID , Sum (QTY) as SQTY
From SP Join S where Level $\gt$ 10 AND Sum (QTY) $\gt$ 1000
Group By SID
گزینه 3 صحیح است.
علت رد گزینه 1 و 2: در این دو گزینه از صفت SQTY استفاده شده که این صفت در هیچیک از دو جدول S و SP وجود ندارد.
علت رد گزینه 4: این گزینه خطای نحوی دارد. زیرا نباید در قسمت where از توابع تجمعی استفاده کرد.
دشوار
دستور Assertion زیر چه محدودیتی را بیان مینماید؟
زبان و پرس و جوی SQL
تولیدکنندگان S(SID, SName, Level, City)
قطعات P(PID, PName, Weight)
قطعات تولیدی SP (SID, PID, QTY)
توسط تولیدکنندگان
Create Assertion Myconst
Check (Not Exists(select *From S Where S.Level < 5 And Exists (select * From SP where SP.SID = S.SID AND SP.PID= 'Pl'))
1 تولیدکنندگان با سطح کمتر از 5 نباید قطعات با شناسه P1 را تولید کنند.
2 فقط تولیدکنندگان با سطح کمتر از 5 میتوانند قطعات با شناسه P1 را تولید کنند.
3 تولیدکنندگان با سطح کمتر از 5 باید حداقل یک قطعه با شناسه P1 را تولید نمایند.
4 هر تولیدکنندهای که قطعه با شناسه P1 را تولید میکند نباید سطحی بیشتر از 5 داشته باشد.
گزینه 1 صحیح است.
از Assertion برای بیان محدودیتها در دیتابیس استفاده میشود.این دستور بیان میکند که تولید کنندهای با سطح کمتر از 5 که قطعات با شناسه P1 را تولید میکنند نباید وجود داشته باشد. یعنی تولیدکنندگان با سطح کمتر از 5 نباید قطعات با شناسه P1 را تولید کنند.
دشوار
بر فرض اینکه $R_1$ و $R_2$ دو رابطه باشند که هیچ صفت مشترکی نداشته باشند، اگر $CK_1$ تنها کلید کاندید رابطه $R_1$ و $CK_2$ تنها کلید رابطه $R_2$ باشد، آنگاه کلید کاندید رابطۀ حاصل از ضرب کارتزین $R_1$ و $R_2$ (یعنی $R_1 \times R_2$)، کدام است؟
پایگاه داده رابطهای
1 ${CK}_\mathrm{1}\cap{CK}_\mathrm{2}$
2 ${CK}_\mathrm{1}\cup{CK}_\mathrm{2}$
3 ${CK}_\mathrm{1}\times{CK}_\mathrm{2}$
4 $CK_2$ و $CK_1$ هر دو کلید کاندید رابطه حاصل هستند.
گزینه 2 صحیح است.
علت رد گزینه 1: چون در صورت سوال گفته شده که این دو رابطه صفت مشترکی ندارند، پس اشتراک این دو کلید کاندید تهی است.
علت رد گزینه 3: چیزی که مهم است وجود یا عدم وجود یک صفت در کلید کاندید است، نه محل قرارگیری آن صفت در کلید کاندید.
علت رد گزینه 4: این گزینه نمیتواند درست باشد زیرا ممکن است در جدول حاصل از ضرب کارتزین دو رابطه $R_1$ و $R_2$، چند سطر با مقادیر یکسان $CK_1$ یا $CK_2$ ظاهر شود که این با مفهوم کلید کاندید در تناقض است.
تست های درس مدارهای منطقی کنکور کامپیوتر ۱۳۹۶ به همراه پاسخ نامه تشریحی
متوسط
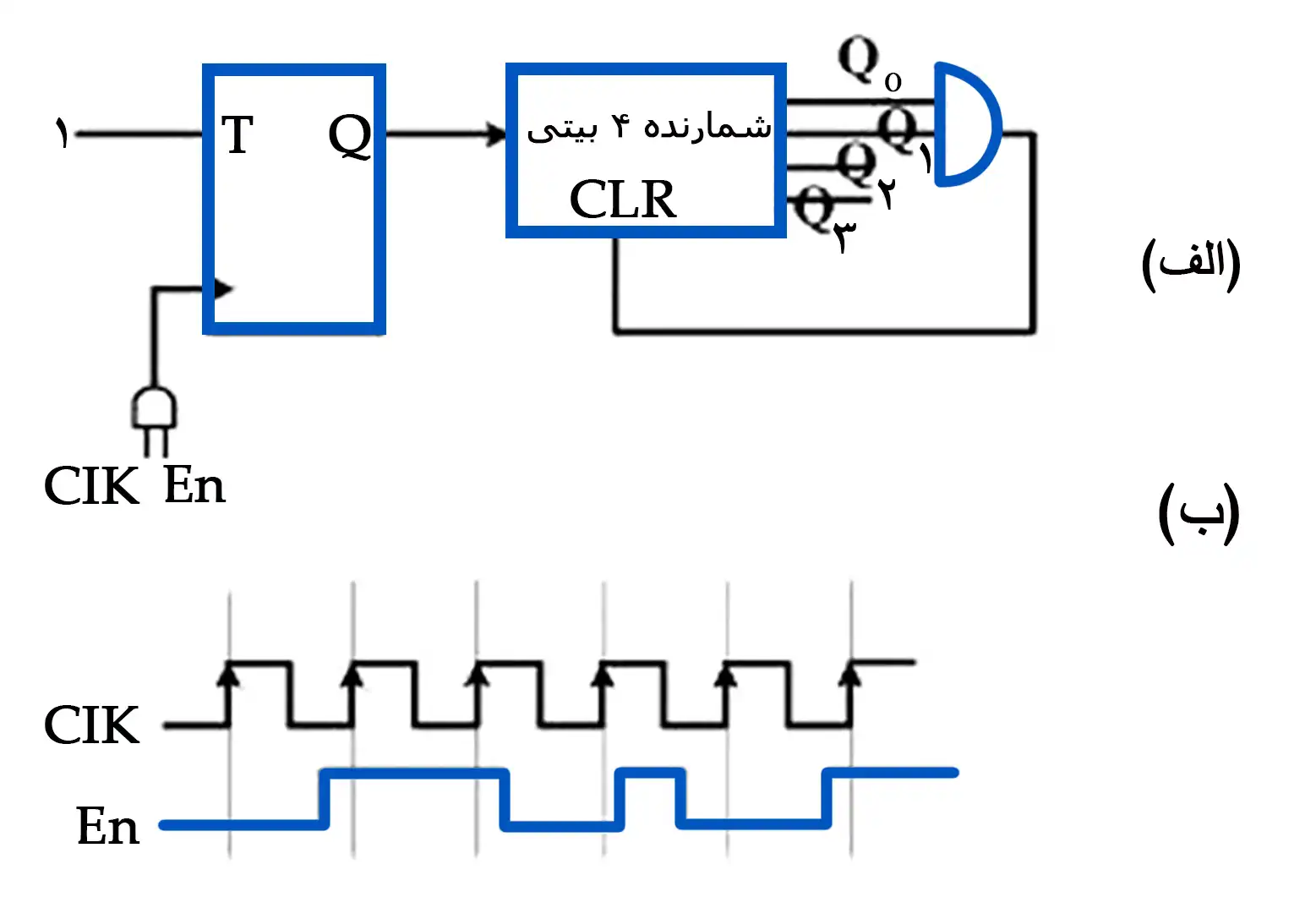
در مدار (الف) اگر مقدار اولیه شمارنده 4 بیتی (خروجی) و FF تماماً صفر باشد، مقدار خروجی در صورت اعمال شکل موج (ب) کدام است؟
تحلیل مدارات ترتیبی و پارامترهای زمانی فلیپ فلاپها
1 $\circ\circ\circ\circ$
2 $\circ\circ\circ1$
3 $\circ\circ1\circ$
4 $\circ1\circ\circ$
برای تاثیر دادن سیگنال EN کافیست تنها پالسهای ساعتی را در نظر بگیریم که در $EN=۱$ رخ دادهاند. در این صورت میتوان مشاهده کرد که ۳ پالس ساعت را باید در نظر گرفت. حال مقدار بیتها را بر حسب پالس ساعت رسم میکنیم:
$\displaystyle \begin{matrix} Q\\ Q_{۳}Q_{۲}Q_{۱}Q_{0}\\CLR \end{matrix}\rightarrow\begin{matrix} 0\\ 0000\\0\end{matrix}\rightarrow\begin{matrix} 1\\ 0001\\0\end{matrix}\rightarrow\begin{matrix} 0\\ 0001\\0\end{matrix}\rightarrow\begin{matrix} 1\\ 0010\\0\end{matrix}$
پس بعد از ۳ پالس ساعت، خروجی ۰۰۱۰ میشود.
بنابراین گزینه ۳ صحیح است.
متوسط
کدام مورد، پیادهسازی تابع منطقی $F(A,B,C)=\sum (1,2,3,6)$ است؟
مدارات ترکیبی
1 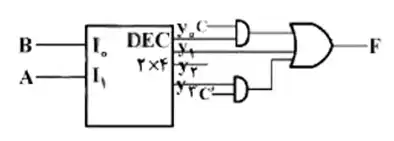
2 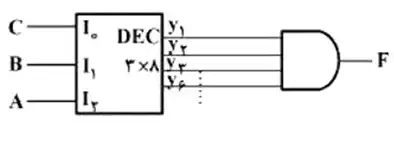
3 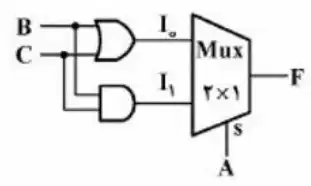
4 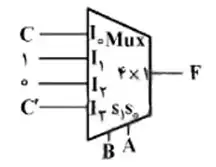
برای حل این سوال از جایگذاری استفاده می کنیم:
گزینه ۲: همواره ۰ است پس نمی تواند درست باشد (زیرا چند خروجی دیکودر به گیت $AND$ متصل هستند). رد گزینه 2
گزینه 3: اگر $A=0$ و یک یا هردوی B و C یک باشند، آنگاه خروجی این مدار 1 خواهد شد. یعنی برای ورودی های ۱، ۲ و ۳ خروجی یک میشود که درست است. اما اگر $A=1$ باشد، برای ۱ شدن خروجی باید $BC=11$ باشند. این یعنی برای ورودی ۶ خروجی ۱ نخواهد شد و غلط است. رد گزینه 3
گزینه ۴: اگر قرار دهیم $AB=10$ آنگاه خروجی یک می شود؛ این بدان معناست که با ورودیهای 4 و 5 (مقادیر مختلف $C$) خروجی این مدار را برابر یک خواهد شد. رد گزینه 4
بنابراین گزینه ۱ صحیح است.
آسان
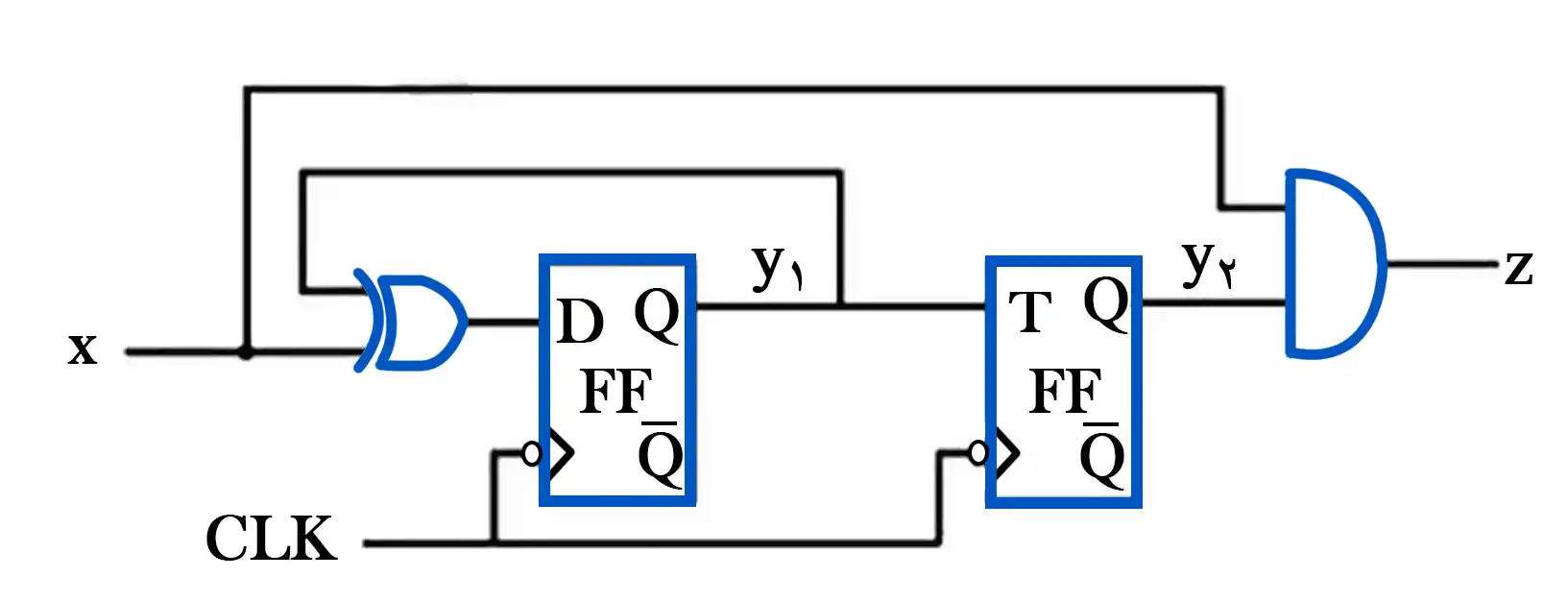
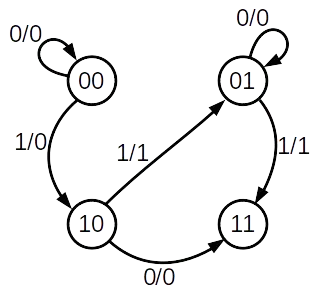
نمودار حالت برای مدار ترتیبی شکل زیر، در کدام حالتهای فعلی فلیپفلاپها دارای لوپ (حلقه بازگشت به حالت فعلی) است؟ (ترتیب حالتها $y_1y_2$ است).
تحلیل مدارات ترتیبی و پارامترهای زمانی فلیپ فلاپها
1 $1 \circ , \circ \circ $
2 $ \circ 1, \circ \circ $
3 $1 \circ , \circ 1$
4 $11,1 \circ $
خواسته سوال این است که برای کدام حالت $y_1y_2$ امکان به وجود آمدن لوپ وجود دارد. در چنین سوالاتی سریعترین راه، بررسی گزینه هاست.
واضح است که ۰۰ می تواند ایجاد لوپ کند. کافیست $x=0$ در نظر بگیریم. در این صورت کلا هیچ مقداری در مدار تغییر نخواهد کرد و در ۰۰ خواهد ماند. همچنین باز هم واضح است که اگر حالت ۰۱ باشد آنگاه با $x=0$ باز مدار در این حالت خواهند ماند. برای درک بهتر نمودار حالت مدار در پایین آورده شده:
بنابراین گزینه ۲ صحیح است.
آسان
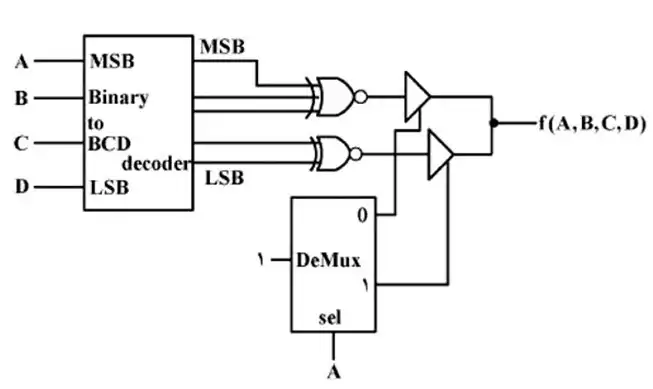
مدار شکل زیر کدام تابع را پیادهسازی میکند؟
مدارات ترکیبی
1 f (A, B, C, D) = $\sum$m(0, 3, 14)
2 f (A, B, C, D) = $\prod$M(5, 6, 9, 11, 12)
3 f (A, B, C, D) = $\prod$M(4, 5, 6, 8, 9, 11, 12)
4 f (A, B, C, D) = $\sum$m(0, 1, 2, 3, 8, 10, 13, 14)
بهترین راه برای حل این سوال، جایگذاری اعداد در مدار می باشد. همچنین رسم جدول کارنو نیز یکی از راه حلهای ممکن می باشد ولی بیش از حد وقتگیر است.
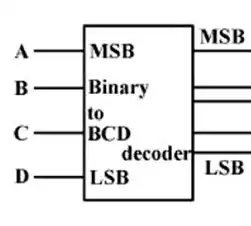
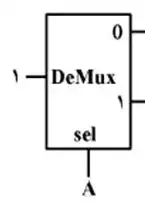
ابتدا توضیح مختصری در مورد قطعات استفاده شده میدهیم:
شکل بالا مربوط به یک دیکودر Binary به BCD است. همانطور که میدانیم برای نشان دادن اعداد ۱۰ تا ۱۶ در BCD به ۵ بیت نیاز است. شکل زیر نیز مربوط به یک DeMux است. یعنی با ۰ شدن مقدار A ورودی را به پورت ۰ وصل می کند و مقدار پورت ۱ را ۰ می کند. برای A=1 نیز برعکس آن.
حال به حل سوال میپردازیم. باید اعدادی را بررسی کنیم که حداقل یکی از گزینه ها را حذف کنند. در گزینهها دو SoP و دو PoS داریم. ابتدا یکی از SoP ها را حذف میکنیم. کوچکترین عددی که در آن اختلاف دارند عدد ۱ است. با جایگذاری $ABCD=0001$ در مدار میتوان متوجه شد که خروجی ۱ میشود. پس عدد ۱ در Mintermها موجود است. رد گزینه 1
کوچکترین عددی که دو Maxterm در آن باهم اختلاف دارند، عدد ۴ است. با جایگذاری $ABCD=0100$ در مدار، خروجی 0 بدست می آید. رد گزینه 2
حال تنها گزینههای باقی مانده، گزینههای 3 و ۴ میباشند. برای مقایسه این دو باید عددی را یافت که در هر دو باشد یا در هیچکدام نباشد. کوچکترین عدد با این خصوصیات عدد ۷ میباشد ولی چون بررسی مدار برای عدد ۸ سادهتر بوده و خاصیت گفته شده را نیز دارد، آن را بررسی میکنیم. با جایگذاری $ABCD=1000$ خروجی ۱ بدست میآید. رد گزینه 3
بنابراین گزینه ۴ صحیح است.
آسان
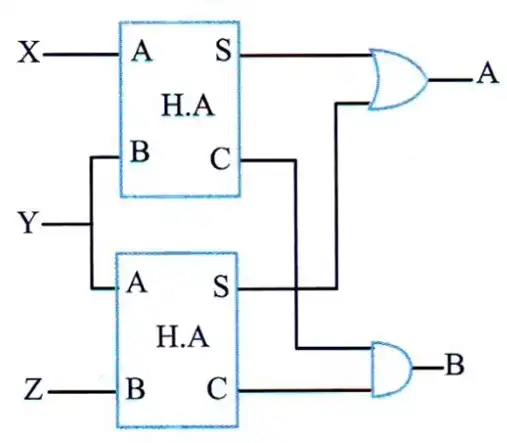
در مدار زیر با توجه به ورودیهای داده شده، شکل صحیح A و B کدام است؟
مدارات ترکیبی
1 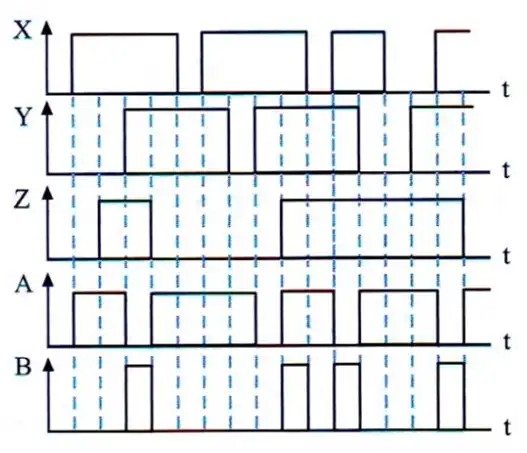
2 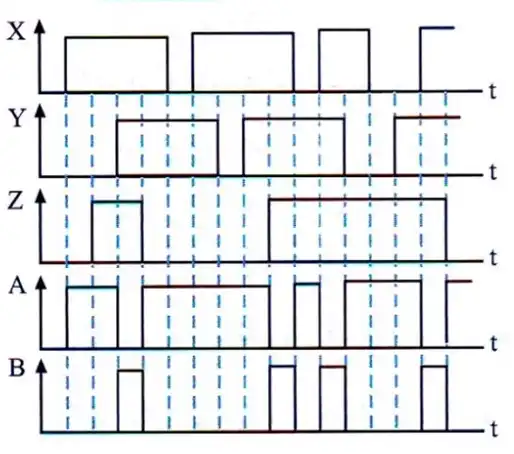
3 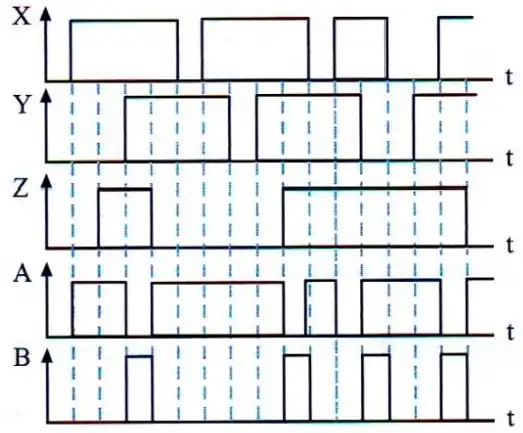
4 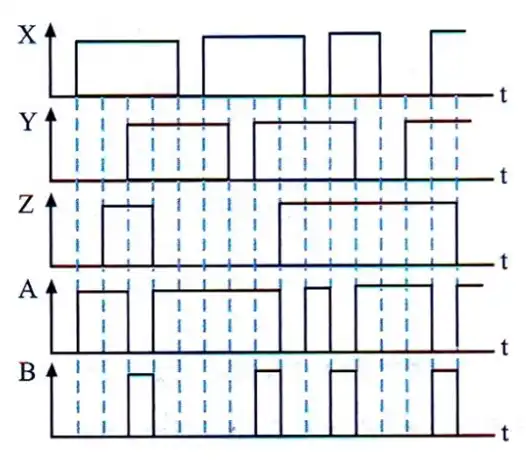
همانطور که از شکل مشخص است برای ۱ شدن خروجی B باید هر دو بیت carry یک شده که این هم یعنی باید همه ورودیها (X و Y و Z) ۱ شوند. در گزینه ۴ در لحظه 8 و در گزینه ۳ در لحظه ۱۳ از زمان مقدار B به اشتباه ۱ شده است. رد گزینه 3 و 4
حال برای A نیز میتوان گفت باید یکی از بیتهای Sum یک شوند که این یعنی باید حداقل یکی از ورودیها ۰ بوده ولی همه آنها نیز ۰ نباشند. این نیز بدان معناست که زمانی که $B=0$ و همه ورودیها ۰ نباشند این خروجی یک خواهد شد. در گزینه ۱ در لحظه ۹ از زمان، B و A هر دو همزمان ۱ شدهاند که غلط است. رد گزینه 1
بنابراین گزینه ۲ صحیح میباشد.
تست های درس سیگنال ها و سیستم ها کنکور کامپیوتر ۱۳۹۶ به همراه پاسخ نامه تشریحی
متوسط
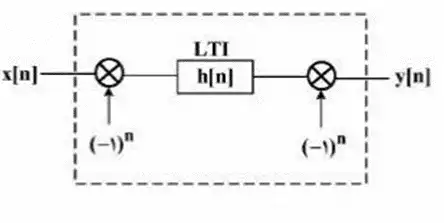
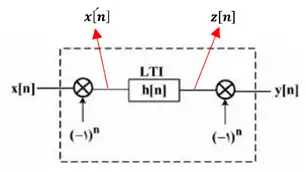
کدام مورد در خصوص سیستم گسسته زیر درست است؟
تحلیل سیستمهای LTI
1 خطی _ تغییر ناپذیر با زمان
2 خطی _ تغییر پذیر با زمان
3 غیر خطی _ تغییر پذیر با زمان
4 غیر خطی _ تغییر ناپذیر با زمان
گزینه 1 صحیح است.
برای سادگی در حل ابتدا میتوانیم عملیاتی که در شکل انجام شده را به حوزهی فرکانس منتقل کنیم.
$\acute{x\left[n\right]}=x\left[n\right]{\left(-1\right)}^n\ {{\stackrel{\ \ \ \ \ \ \ \ \ \ \ \ \ \ Z\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }{\Longrightarrow}}}\ \acute{X(z)}\ =\ X(\frac{z}{-1})\ =\ X(-z)$
$z\left[n\right]=\acute{x\left[n\right]}*h\left[n\right]\stackrel{\ \ \ \ \ \ \ \ \ \ \ \ \ \ Z\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }{\Longrightarrow}\ Z(z)\ =\ \acute{X(z)}H(z)\ $
$y\left[n\right]=z\left[n\right]{\left(-1\right)}^n\ \stackrel{\ \ \ \ \ \ \ \ \ \ \ \ \ \ Z\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }{\Longrightarrow}\ Y(z)\ =\ Z(-z)\ \ \ \longrightarrow \ Y(z)\ =\ \acute{X(-z)}H(-z)\ =\ X(z)H(-z)\ $
با توجه به رابطه بدست آمده برای خروجی مشخص میشود که سیستم داده شده، سیستمی LTI با پاسخ ضربهی $h_T[n] = h[n](-1)^n$ است.
آسان
سیستم $y\left[n\right]=\sum _{k=-\infty}^{\infty}x[k]x[n+k]$ ، چه نوع سیستمی است؟
سیستمها
1 خطی _ علّی و پایدار
2 غیر خطی _ غیر علّی و پایدار
3 غیر خطی _ غیر علّی و ناپایدار
4 خطی _ علّی و ناپایدار
گزینه 3 صحیح است.
بررسی علی بودن: از روی رابطه داده شده برای سیستم متوجه میشویم که:
$\forall n\in \mathbb{N}\mathrm{,} \ \ \ \ \ \mathrm{\ }\mathrm{\ }y[n]\ \propto \ x[n\ +\ k]\ {{\stackrel{If\ n\ =\ 2\ \&\ k\ =\ 1}{\Longrightarrow}}}\ y[2]\ \propto \ x[3]$
به ازای مثال نقض گفته شده، چون خروجی سیستم در یک لحظه، به ورودی در لحظات بعد از آن وابسته شده در نتیجه سیستم علی نیست.(دقت کنید که وقتی سیستمی علی نباشد(غیر علی باشد)، نمیتوان گفت آن سیستم ضد علی است.)
بررسی خطی بودن: برای بررسی خطی بودن سیستم در ابتدا خاصیت همگنی آن را چک میکنیم:
$T[ax[n]]\ =\ \sum^{+\infty }_{k\ =\ -\infty }{ax[k]ax[n\ +\ k]}\ =\ a^2\sum^{+\infty }_{k\ =\ -\infty }{x[k]x[n\ +\ k]}\ \boldsymbol{\neq }\ ay[n]\ =a\ \sum^{+\infty }_{k\ =\ -\infty }{x[k]x[n\ +\ k]}$
خاصیت همگنی برقرار نیست در نتیجه سیستم خطی نیست.
در مورد پایداری در صورتی سیستم پایدار تعریف میشود که به ازای ورودی محدود خروجی محدود باشد(Bounded input Bounded out put) یعنی نباید به ازای ورودی متناهی خروجی بی نهایت شود در این سوال خیلی واضح است که اگر مقدار x برابر یک عدد ثابت مثلا عدد 1 در نظر بگیریم حاصل سیگما از منفی تا مثبت بی نهایت برابر بی نهایت خواهد شد و نامتناهی است لذا به سادگی مشخص است که ناپایدار است.
آسان
در خصوص خواص یک سیستم زمان _ پیوسته با رابطۀ ورودی _ خروجی $y\left(t\right)=x(\cos{t)}$ ، کدام خاصیت را دارا نیست؟
سیستمها
1 غیر خطی
2 غیر علی
3 تغییر پذیر با زمان
4 معکوس ناپذیر
گزینه 1 صحیح است.
بررسی خطی بودن: برای خطی بودن سیستم باید رابطه زیر برای آن برقرار باشد:
$T[ax_1(t)\ +\ bx_2(t)] = aT[x1(t)] + bT[x2(t)] $
$T\left[ax_1(t)+bx_2(t)\right]=ax_1\left(cos{t}\right)+bx_2\left(cos{t}\right)=aT\left[x_1(t)\right]+bT\left[x_2(t)\right]$
پس سیستم خطی است. (یا به عبارتی سیستم فاقد خاصیت غیرخطی بودن است.)
بررسی علی بودن: برای اینکه نشان دهیم سیستم غیر علی است کافیست مثال نقض برای آن بیاوریم:
$If\ \ t=0\longrightarrow y\left(0\right)=x\left(\cos{0}\right)=x\left(1\right)$
مثال نقض فوق نشان میدهد که خروجی در لحظه 0 به ورودی در لحظه 1 وابسته است. در نتیجه سیستم داده شده غیر علی است.(دارای خاصیت غیر علی است.)
بررسی تغییر ناپذیر بودن با زمان: برای TI بودن سیستم باید رابطه زیر برای آن برقرار باشد:
$T\left[x\left(t+t_0\right)\right]=y\left(t+t_0\right)$
$T[x(t\ +\ t_0)] = x(cost + t_0) ≠ y(t + t_0) = x(cos(t + t_0)) $
در نتیجه سیستم تغییرپذیر با زمان است.
بررسی معکوس پذیری: شرط لازم جهت معکوس پذیر بودن سیستم این است که همه زمانها در آرگومان ورودی ساخته شده و در خروجی نقش داشته باشند. در ضابطه داده شده آرگومان x تنها میتواند مقادیر بین 1 و 1- را به خود بگیرد در نتیجه میتوان گفت که سیستم معکوس ناپذیر است.
متوسط
کدام مورد پاسخ پلۀ سیستمی به سیگنال ورودی $\mathrm{x}\left(\mathrm{t}\right)\mathrm{=\partial}\left(\mathrm{t-1}\right)\mathrm{+2\partial(t-2)}$ که در شکل نشان داده شده است؟
تحلیل سیستمهای LTI
1 
2 
3 
4 
گزینه 2 با تاثیر مثبت صحیح است.
با توجه به خواسته و فرض سوال میبایست در صورت LTI بودن سیستم ذکر میشد اما با این وجود میتوان حدس زد که منظور طراح سیستم LTI است.
میدانیم که در یک سیستم LTI رابطه ورودی و خروجی به صورت زیر است:
$y\left(t\right)=x\left(t\right)\ast h\left(t\right)$
$h(t)\ =\ \frac{ds(t)}{dt} $
$y\left(t\right)=h\left(t\right)\ast\left[\delta\left(t-1\right)+2\delta\left(t-2\right)\right]=h\left(t-1\right)+2h\left(t-2\right)$
حال باید از روی نمودار پاسخ پله داده شده، نمودار پاسخ ضربه سیستم را بدست آوریم. برای بدست آوردن پاسخ پله باید از نمودار پاسخ پله مشتق بگیریم که حاصل به صورت زیر بدست میآید:
حال از روی نمودار بدست آمده، راحتی میتوان نمودار خروجی را به صورت زیر بدست آورد:
در نهایت حاصل جمع دو نمودار بالا، پاسخ را به ما میدهد:
متوسط
سیستم زمان پیوسته و $LTI$ با معادله دیفرانسیل $\frac{\mathrm{dy(t)}}{\mathrm{dt}}\mathrm{+2y}t=x(t)$ توصیه شده است. پاسخ سیستم به ورودی $x\left(t\right)=e^{-t}u(t)$ کدام است؟
تحلیل سیستمهای LTI
1 $\left(\mathrm{2}\mathrm{e}^{\mathrm{-t}}\mathrm{+2} \mathrm{e}^{\mathrm{-2t}}\right)\mathrm{u(t)}$
2 $\left(\mathrm{2}\mathrm{e}^{\mathrm{-t}}\mathrm{-} \mathrm{e}^{\mathrm{-2t}}\right)\mathrm{u(t)}$
3 $\left(\mathrm{e}^{\mathrm{-t}}\mathrm{-} \mathrm{e}^{\mathrm{-2t}}\right)\mathrm{u(t)}$
4 $\left(\mathrm{e}^{\mathrm{-t}}\mathrm{+} \mathrm{e}^{\mathrm{-2t}}\right)\mathrm{u(t)}$
گزینه 3 صحیح است.
با توجه به این که سیستم زمان پیوسته است و رابطه سیستم به صورت معادله دیفرانسیلی داده شده، بهتر است از تبدیل لاپلاس برای حل آن استفاده کنیم:
$\frac{dy\left(t\right)}{dt}+2y\left(t\right)=x\left(t\right){{\stackrel{\ \ \ \ \ \ \ \ \ \ \mathcal{L}\ \ \ \ \ \ \ \ \ }{\Longrightarrow}}}SY\left(s\right)+2Y\left(s\right)=X\left(s\right)\longrightarrow Y\left(s\right)\left(s+2\right)=X\left(s\right)$
$H\left(s\right)=\frac{Y\left(s\right)}{X\left(s\right)}=\frac{1}{s+2}\ \ \ \ \ \ \ ,\ ROC\left[H\left(s\right)\right]=\{Re\left[s\right]\gt 2\ \ \ \ \ or\ \ \ \ \ Re\left[s\right]\lt -2\}$
$x(t)\ =\ e^{-t}u(t)\ {{\stackrel{\ \ \ \ \ \ \ \ \ \ \mathcal{L}\ \ \ \ \ \ \ \ }{\Longrightarrow}\ }}X(s)\ =\ \frac{1}{s\ +\ 1}\ \ \ \ \ \ ,Re[s]\gt -1$
$Y\left(s\right)=X\left(s\right)H\left(s\right)=\frac{1}{\left(s+1\right)\left(s+2\right)}$
$,ROC\{Y(s)\}\ =\{\ Re[s]\gt -1\ \}\ \cap \ \{Re\left[s\right]\gt 2\ \ \ \ \ or\ \ \ \ \ Re\left[s\right]\lt -2\}\ =\ \{Re[s]\gt -1\}\ $
حال با استفاده از تفکیک کسر باید پاسخ سیستم را محاسبه کنیم:
$Y\left(s\right)=\frac{1}{\left(s+1\right)\left(s+2\right)}=\frac{A}{s\ +\ 1}+\frac{B}{s\ +\ 2}{{\stackrel{\times \left(s+1\right)}{\longrightarrow}}}Y\left(s\right)\left(s+1\right)=\frac{1}{s\ +\ 2}=A+B\frac{s\ +\ 1}{s\ +\ 2}{{\ \ \stackrel{s\ =\ -1}{\longrightarrow}\ \ }}A=1$
$Y\left(s\right)=\frac{1}{\left(s+1\right)\left(s+2\right)}=\frac{A}{s\ +\ 1}+\frac{B}{s\ +\ 2}{{\stackrel{\times \left(s+2\right)}{\longrightarrow}}}Y\left(s\right)\left(s+2\right)=\frac{1}{s\ +\ 1}=B+A\frac{s\ +\ 2}{s\ +\ 1}{{\ \ \stackrel{s\ =\ -2}{\longrightarrow}\ \ }}B=-1$
$Y\left(s\right)=\frac{1}{s\ +\ 1}-\frac{1}{s\ +\ 2},Re\left[s\right]>-1{{\stackrel{\ \ \ \ \ \ \ \ \ \ {\mathcal{L}}^{-1}\ \ \ \ \ \ \ \ }{\Longrightarrow}}}y\left(t\right)=e^{-t}u\left(t\right)-e^{-2t}u\left(t\right)=\left(e^{-t}-e^{-2t}\right)u\left(t\right)$
متوسط
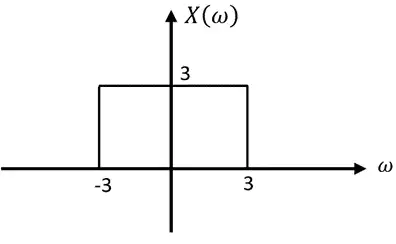
بین سیگنال $x(t)$ (با تبدیل فوریه $\mathrm{X}\left(\mathrm{j\omega}\right)\mathrm{=3u}\omega+3-3u(\omega-3)$ و سیگنال $v(t)$ رابطۀ $\mathrm{x}\left(\mathrm{t}\right)\mathrm{=v}(t)cos(\frac {3}{2}t)$ برقرار است. سیگنال $v(t)$ کدام است؟
تبدیل فوریه
1 $\mathrm{6}\mathrm{sinc}{\left(\frac{\mathrm{3}}{\mathrm{2\pi}}\mathrm{t} \right)\mathrm{cos(} \frac{\mathrm{3} }{\mathrm{2}}\mathrm{t)} }$
2 $\mathrm{6}\mathrm{sinc}{\left(\frac{\mathrm{1}}{\mathrm{2\pi}}\mathrm{t} \right)}$
3 $\mathrm{6}\mathrm{sinc}{\left(\frac{\mathrm{3}}{\mathrm{ \pi}}\mathrm{t} \right)}$
4 $\mathrm{6}\mathrm{sinc}{\left(\frac{\mathrm{3}}{\mathrm{2\pi}}\mathrm{t} \right)}$
گزینه 4 صحیح است.
با تبدیل سیگنال ورودی به سیگنالی معادل و آشنا میتوانیم از خواص تبدیل فوریه به صورت زیر در این سوال استفاده کنیم:
$X\left(\omega\right)=3u\left(\omega+3\right)-3u\left(\omega-3\right)$
شاید در نگاه اول نتوان سیگنالِ معادلِ عبارت فوق را که تبدیل فوریهش برای شما راحت است، تشیخص دهید. اما به توجه به ضابطه، رسم این سیگنال ساده بوده و در تشخیص سیگنال مورد نظر به شما کمک میکند:
با رسم این سیگنال متوجه میشویم که سیگنالی مربعی است که عکس تبدیل فوریه آن را نیز میدانیم:
$X\left(\omega \right)=3\prod{\left(\frac{\omega }{2\times 3}\right)\stackrel{\ \ \ \ \ \ \ \ \ \ {\mathcal{L}}^{-1}\ \ \ \ \ \ \ \ }{\Longrightarrow}}x\left(t\right)=\frac{3{\mathrm{sin} 3t\ }}{\pi t}=\frac{3}{\pi t}{\mathrm{sin} 3t\ }$
در صورت سوال گفته شده که $x(t)=v(t)cos(\frac {3}{2}t)$ حال برای محاسبه $v(t)$ باید کاری کنیم که عبارت بالا برای ما به شکلی درآید که داخل آن $cos(\frac{3}{2}t)$ وجود داشته باشد. از گذشته میدانستیم که:
$sin \ 2\theta = 2\ sin \theta \ cos\theta$
اکنون از این فرمول در $x(t)$ استفاده میکنیم:
$x\left(t\right)=\frac{3}{\pi t}{\mathrm{sin} 3t\ }=\frac{6}{\pi t}{\mathrm{sin} \frac{3t}{2}\ }{\mathrm{cos} \frac{3t}{2}\ }=v\left(t\right){\mathrm{cos} \frac{3t}{2}\ }\longrightarrow v\left(t\right)=\frac{6}{\pi t}{\mathrm{sin} \frac{3t}{2}\ }$
$Sinc\left(t\right)=\frac{{\mathrm{sin} \pi t\ }}{\pi t}\longrightarrow \frac{6}{\pi }Sinc\left(\frac{t}{\pi }\right)=\frac{6}{\pi t}{\mathrm{sin} t\ }{{\stackrel{t\longrightarrow \frac{3}{2}t}{\longrightarrow}}}\frac{6}{\pi \frac{3t}{2}}{\mathrm{sin} \frac{3t}{2}\ }=\frac{9}{\pi }\frac{{\mathrm{sin} \frac{3t}{2}\ }}{\frac{3t}{2}}=\frac{9}{\pi }Sinc\left(\frac{3t}{2\pi }\right)$
$v\left(t\right)=\frac{9}{\pi }Sinc\left(\frac{3t}{2\pi }\right)$
.
همانطور که مشاهده میکنید پاسخ در گزینهها نیست. به همین دلیل گزینه4 با تاثیر مثبت اعلام شد
متوسط
ورودی یک سیستم زمان گسسته $LTI$ با پاسخ ضربه $\mathrm{h}\left[\mathrm{n}\right]\mathrm{=}(\frac {1}{3})^nu[n]$ به صورت $x\left[n\right]={(-\frac{1}{3})}^n$ است. خروجی این سیستم در لحظه $n=2$ ، کدام است؟
تحلیل سیستمهای LTI
1 $\frac {-1}{6}$
2 $\frac {1}{9}$
3 $\frac {1}{18}$
4 $1$
گزینه 3 صحیح است.
چون سیستم LTI است پس داریم:
$y[n]=H(z)|_{z=-\frac{1}{3}}× \left (-\frac{1}{3} \right )^n$
$h\left[n\right]={\left(\frac{1}{3}\right)}^nu\left[n\right]\stackrel{\ \ \ \ \ \ \ \ \ \ \ \ \ \ Z\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }{\Longrightarrow}H\left(z\right)=\frac{1}{1\ -\ \frac{1}{3}z^{-1}}\ \ \ \ \ \ \ ,\left|z\right|\gt \frac{1}{3}$
$H\left(z\right)|_{z\ =\ -\ \frac{1}{3}}=\frac{1}{1-\frac{1}{3}\left(-3\right)}=\frac{1}{2}$
در نتیجه پاسخ سیگنال در لحظه n = 2 به صورت زیر محاسبه میشود:
$y\left[n\right]=\frac{1}{2}\left(-\frac{1}{3}\right)^n\longrightarrow y\left[2\right]=\frac{1}{2}\left(-\frac{1}{3}\right)^2=\frac{1}{18}$
متوسط
سیستمی با ورودی $x(t)$ و خروجی $y(t)$ و رابطه $y\left(t\right)=\int_{\mathrm{t-1}}^{t}{\mathrm{cos}{\left(\mathrm{2\pi\alpha}\right)}\mathrm{x} \left(\mathrm{\alpha}\right)\mathrm{d\alpha} }$ چه نوع سیستمی است؟
سیستمها
1 تغییر پذیر با زمان و معکوس ناپذیر
2 تغییر ناپذیر با زمان و معکوس ناپذیر
3 تغییر پذیر با زمان و معکوس پذیر
4 تغییر ناپذیر با زمان و معکوس پذیر
گزینه 1 صحیح است.
بررسی تغییرپذیری با زمان: برای TIبودن سیستم باید رابطه زیر برای آن برقرار باشد:
$T\left[x\left(t+t_0\right)\right]=y\left(t+t_0\right)$
$T\left[x\left(t+t_0\right)\right]=\int^t_{t-1}{{\mathrm{cos} \left(2\pi \alpha \right)\ }x(\alpha +\ t_0)}d\alpha {{\stackrel{\alpha +\ t_0\ \longrightarrow \ \tau }{\Longrightarrow}}}\ \int^t_{t-1}{{\mathrm{cos} \left(2\pi (\tau -\ t_0)\right)\ }x(\tau )}d\tau $
$y\left(t+t_0\right)=\ \int^{t+\ t_0}_{t-1+\ t_0}{{\mathrm{cos} \left(2\pi \alpha \right)\ }x(\alpha )}d\alpha \ \Longrightarrow \ y\left(t+t_0\right)\neq \ T\left[x\left(t+t_0\right)\right]$
پس سیستم تغییر پذیر با زمان است.
بررسی معکوس پذیری: شرط لازم جهت معکوس پذیر بودن سیستم این است که همه زمانها در آرگومان ورودی ساخته شده و در خروجی نقش داشته باشند. در این ضابطه به ازای نقاطی که $cos (2\pi \alpha)$ برابر $0$ میشود، ورودی در ساخت خروجی نقش ندارد در نتیجه سیستم معکوس ناپذیر است.
دشوار حاصل انتگرال $\int_{-\infty}^{\infty}{\frac{\mathrm{sin}{\left(\mathrm{\omega}\right)}\mathrm{sin(2\omega)} }{\mathrm{\omega}^\mathrm{2}}d\omega}$ ، کدام است؟ تبدیل فوریه
1 $1$
2 $2$
3 $\pi$
4 $2\pi$
گزینه 3 صحیح است.
برای محاسبه حاصل انتگرال باید آن را به فرمولی که حفظ هستیم و محاسبه آن راحتتر است، تبدیل کنیم. طبق رابطه اصلی تبدیل فوریه یک سیگنال داریم:
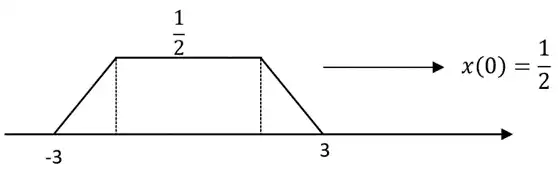
$x\left(t\right)=\frac{1}{2\pi }\ \int^{+\infty }_{-\infty }{X\left(\omega \right)e^{j\omega t}d\omega }\ {{\stackrel{t\ =0}{\Longrightarrow}\ }}2\pi x\left(0\right)=\ \int^{+\infty }_{-\infty }{X\left(\omega \right)d\omega }$
حال اگر فرض کنیم $X(\omega)=\frac {sin(\omega)sin(2\omega)}{\omega^2}$ باشد، گویی برای محاسبه حاصل انتگرال باید حاصل معکوس تبدیل فوریه $X(\omega)=\frac {sin(\omega)sin(2\omega)}{\omega^2}$ در نقطه $0$ را محاسبه کرده و حاصل را در $2\pi$ ضرب کنیم. حال میبایست به صورت زیر عمل کنیم:
$X\left(\omega \right)=\ \frac{{\mathrm{sin} \left(\omega \right)\ }{\mathrm{sin} \left(2\omega \right)\ }}{{\omega }^2}=\ \frac{{\mathrm{sin} \left(\omega \right)\ }}{\omega }\times \frac{{\mathrm{sin} \left(2\omega \right)\ }}{\omega }=\ X_1\left(\omega \right)X_2\left(\omega \right)\ {{\stackrel{\ \ \ \ \ \ \ \ \ \ {\mathcal{F}}^{-1}\ \ \ \ \ \ }{\Longrightarrow}}}\ x_1\left(t\right)*x_2\left(t\right)$
$X_1\left(\omega \right)=\ \ \frac{{sin \left(\omega \right)\ }}{\omega }\ {{\stackrel{\ \ \ \ \ \ \ \ \ \ {\mathcal{F}}^{-1}\ \ \ \ \ \ }{\Longrightarrow}}}\ x_1\left(t\right)=\ \frac{1}{2}\prod \left(\frac{t}{2\times 1}\right)$
$X_2\left(\omega \right)=\ \ \frac{{sin \left(2\omega \right)\ }}{\omega }\ {{\stackrel{\ \ \ \ \ \ \ \ \ \ {\mathcal{F}}^{-1}\ \ \ \ \ \ }{\Longrightarrow}}}\ x_2\left(t\right)=\ \frac{1}{2}\prod \left(\frac{t}{2\times 2}\right)$
$x\left(t\right)=\ x_1\left(t\right)*x_2\left(t\right)=\frac{1}{2}\prod \left(\frac{t}{2\times 1}\right)\ *\ \ \frac{1}{2}\prod \left(\frac{t}{2\times 2}\right)$
سیگنال $x(t)$ به صورت زیر بدست میآید:
$2\pi x(0)= 2\pi × \frac{1}{2}= \pi$
متوسط
پاسخ ضربه یک سیستم زمان پیوسته، به شکل $\mathrm{h}\left(\mathrm{t}\right)\mathrm{=\delta}\left(\mathrm{2t}\right)\mathrm{+\delta(t-1)}$ میباشد. پاسخ این سیستم به ورودی $\mathrm{x}\left(\mathrm{t}\right)\mathrm{=sin(2}\left(\mathrm{t-1}\right)\mathrm{)}$ ، کدام است؟
تحلیل سیستمهای LTI
1 $\mathrm{sin}{\left(\mathrm{2}\left(\mathrm{t-1}\right)\right)}\mathrm{+sin(2}\left(\mathrm{t-2}\right)\mathrm{)}$
2 $\mathrm{sin}{\mathrm{(2t-3)}}\mathrm{+sin(2t-4)}$
3 $\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin} {\mathrm{(2t-3)}}\mathrm{+sin(2t-4)}$
4 $\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin} {\left(\mathrm{2}\left(\mathrm{t-1}\right)\right)}\mathrm{+sin(2}\left(\mathrm{t-2}\right)\mathrm{)}$
گزینه 4 صحیح است.
نکته اول در این تست این است که اگر نگوید سیستم LTI است، سوال قابل حل نیست! پس در اینجا بافرض LTI بودن سیستم سوال را حل میکنیم:
$y\left(t\right)=x\left(t\right)\ast h\left(t\right)=x\left(t\right)\ast\left[\delta\left(2t\right)+\ \delta\left(t-1\right)\right]=\frac{1}{2}x\left(t\right)+x\left(t-1\right)$
$y\left(t\right)=\ \frac{1}{2}\sin{(2(t-1))}+\ \sin{\left(2\left(t-1-1\right)\right)}$
متوسط
در یک سیستم $LTI$ با تابع تبدیل $\mathrm{H}\left(\mathrm{s}\right)\mathrm{=}\frac{\mathrm{s+5} }{\mathrm{s}^\mathrm{2}\mathrm{+4s+4-} \mathrm{k}^\mathrm{2}}$ که در آن $k$ عدد حقیقی است، کدام مورد درست است؟
تحلیل سیستمهای LTI
1 سیستم نمیتواند همزمان سببی و پایدار باشد.
2 سیستم ممکن است هم پایدار و هم سببی باشد.
3 سیستم اگر پایدار باشد، حتماً سببی هم هست.
4 سیستم اگر سببی باشد، حتماً پایدار هم هست.
گزینه 2 صحیح است.
ابتدا قطبهای سیستم را محاسبه میکنیم:
$H\left(s\right)=\ \frac{s+5}{s^2+4s+4-\ k^2}=\ \frac{s+5}{{\left(s+2\right)}^2-\ k^2}\Longrightarrow \ {\left(s+2\right)}^2-\ k^2=0\ \Longrightarrow s_{1,2}=\ \pm k-2\ $
حال با توجه به حالات مختلف k محل قرارگیری قطبها را بررسی میکنیم:
$If\ \ k\ =\ 5\ \ then\ \left\{ \begin{array}{c} s_1\ =\ 3\ \\ s_2\ =\ -7 \end{array} \right.$
در این حالت چون یک قطب سمت چپ محور $j\omega$ و قطب دیگر در سمت راست محور قرار دارد، اگر سیستم علی باشد یعنی $+\infty \in ROC[H(s)]$ است در نتیجه $ROC[H(s)]: Re[s]\gt 3$ میشود و سیستم نمیتواند همزمان علی و پایدار باشد. همچنین اگر فرض کنیم این سیستم پایدار است آنگاه $ROC[H(s)]: 3\gt Re[s]\gt -7$ میشود و این یعنی سیستم نمیتواند علی شود (رد گزینههای 3و4). حال اگر :
$If\ \ k\ =\ 0\ \ then\ \left\{ \begin{array}{c} s_1\ =\ -2\ \\ s_2\ =\ -2 \end{array} \right.$
در این حالت چون هر دو قطب سمت چپ محور $j\omega$ قرار دارد، اگر سیستم علی باشد یعنی $+\infty\in ROC[H(s)]$ است در نتیجه $ROC[H(s)]: Re[s]\gt -2$ میشود و سیستم میتواند همزمان علی و پایدار باشد.(رد گزینهی 1)
دشوار
سیستمی داریم که در آن رابطۀ ورودی – خروجی به صورت $\ \mathrm{y}(t)=\frac {1}{1+t^2}x(t)$ میباشد. اگر ورودی سیستم $x\left(t\right)=\frac{\sin (\omega t)}{\pi t}$ باشد، مقدار $DC$ سیگنال خروجی کدام است؟
تحلیل سیستمهای LTI
1 $0$
2 $1-e^{-\omega}$
3 $e^{-\omega}-1$
4 $e^{-\omega}-e^\omega$
گزینه 2 صحیح است.
مقدار DC سیگنال y برابر $\int_{-\infty}^{+\infty}y(t)dt$ است. با توجه به فرضیات داده شده در سوال عبارت را بازنویسی میکنیم:
$\int_{-\infty}^{+\infty}y\left(t\right)dt\ =\ \int_{-\infty}^{+\infty}{\frac{1}{1\ +\ t^2}\frac{\sin{\left(wt\right)}}{\pi t}dt}$
برای محاسبه حاصل انتگرال باید آن را به فرمولی که حفظ هستیم و محاسبه آن راحتتر است، تبدیل کنیم. طبق رابطه تبدیل فوریه یک سیگنال داریم:
$Y(\omega )\ =\ \int^{+\infty }_{-\infty }{y\left(t\right)e^{-j\omega t}dt}\ {{\stackrel{\omega \ =\ 0}{\Longrightarrow}}}\ Y(0)\ =\ \int^{+\infty }_{-\infty }{y\left(t\right)dt}\ =\int^{+\infty }_{-\infty }{\frac{1}{1\ +\ t^2}\frac{{\mathrm{sin} \left(wt\right)\ }}{\pi t}dt}$
در نتیجه برای محاسبه مقدار DC سیگنال کافیست تبدیل فوریه سیگنال $y(t)$ را در نقطه $0$ پیدا کنیم. تبدیل فوریه سیگنال $y(t)$ به صورت زیر محاسبه میشود:
$y\left(t\right)=\underbrace{\frac{1}{1\ +\ t^2}}_{z\left(t\right)}x\left(t\right)\stackrel{\ \ \ \ \ \ \ \ \ \ \mathcal{F}\ \ \ \ \ \ \ }{\Longrightarrow}\frac{1}{2\pi }Z\left(\omega \right)*X\left(\omega \right)$
محاسبه تبدیل فوریه سیگنال z برای ما آشنا نیست اما عکس تبدیل فوریه آن برای ما آشناست. پس میتوان از روش زیر استفاده کرد:
$\underline{\overline{\left|e^{\alpha \left|t\right|},Re\left[\alpha \right]\gt 0\stackrel{\ \ \ \ \ \ \ \ \ \ \mathcal{F}\ \ \ \ \ \ \ }{\Longrightarrow}\frac{-2\alpha }{{\omega }^2\ +\ {\alpha }^2}\ \ \ \longrightarrow \ \frac{-2\alpha }{t^2\ +\ {\alpha }^2}\stackrel{\ \ \ \ \ \ \ \ \ \ \mathcal{F}\ \ \ \ \ \ \ }{\Longrightarrow}\ 2\pi e^{\alpha \left|\omega \right|}\right|}}$
$\mathcal{F}\left[\frac{-2\alpha }{t^2\ +\ {\alpha }^2}\right]=2\pi e^{\alpha \left|\omega \right|}\longrightarrow \mathcal{F}\left[\frac{1}{t^2\ +\ 1}\right]=\pi e^{-\left|\omega \right|}$
$\mathcal{F}\left[\frac{{\mathrm{sin} \left(wt\right)\ }}{\pi t}\right]=\prod \left(\frac{\omega }{2w}\right)$
با توجه به تعریف کانولوشن داریم:
$Y\left(\omega \right)=\frac{1}{2\pi }\int^{+\infty }_{-\infty }{X\left(\alpha \right)Z\left(\omega -\alpha \right)d\alpha }{{\stackrel{\omega \ =\ 0}{\Longrightarrow}}}Y\left(0\right)=\frac{1}{2\pi }\int^{+\infty }_{-\infty }{X\left(\alpha \right)Z\left(-\alpha \right)d\alpha }=\frac{1}{2\pi }\int^{+\infty }_{-\infty }{\pi e^{-\left|\omega \right|}\prod \left(\frac{\omega }{2w}\right)d\alpha }=\frac{1}{2}\int^{+w}_{-w}{e^{-\left|\omega \right|}d\omega }=\int^w_0{e^{-\omega }d\omega }=1-e^{-\omega }$
آسان
کدام عبارت در خصوص تبدیل فوریه دنباله $\mathrm{x}\left[\mathrm{n}\right]\mathrm{=}3^nu[n-1]+4^nu[-n]$ ، درست است؟
تبدیل فوریه
1 تبدیل فوریه وجود ندارد.
2 تبدیل فوریه همواره وجود دارد.
3 تبدیل فوریه به ازاء $n \ge 1$ وجود دارد.
4 تبدیل فوریه فقط به ازاء $|z| \ge 1$ وجود دارد.
گزینه 1 صحیح است.
برای اینکه یک سیگنال تبدیل فوریه داشته باشد باید شرایط دیریکله در آن برقرار باشد. مهمترین شرط آن مطلقا انتگرال پذیر یا مطلقا جمع پذیر بودن سیگنال است. حال باید چک کنیم که سیگنال داده شده مطلقا جمع پذیر هست یا خیر:
$\sum^{+\infty }_{n\ =\ -\infty }{\left|3^nu\left[n-1\right]+4^nu\left[-n\right]\right|}\ =\ \underbrace{\sum^{+\infty }_{n\ =\ -\infty }{\left|3^nu\left[n-1\right]\right|}}_{+\infty }\ +\ \sum^{+\infty }_{n\ =\ -\infty }{\left|4^nu\left[-n\right]\right|}\ \ =\ \infty $
در نتیجه سیگنال داده شده تبدیل فوریه ندارد.
دشوار
اگر $x[n]$ یک سیگنال گسسته زمان پریود یک با پریود $N=5$ بوده و ضرایب سری فوریه آن به صورت زیر باشد، در این صورت ضرایب سری فوریه سیگنال $(-1)^n x[n]$ کدام است؟
سری فوریه
1 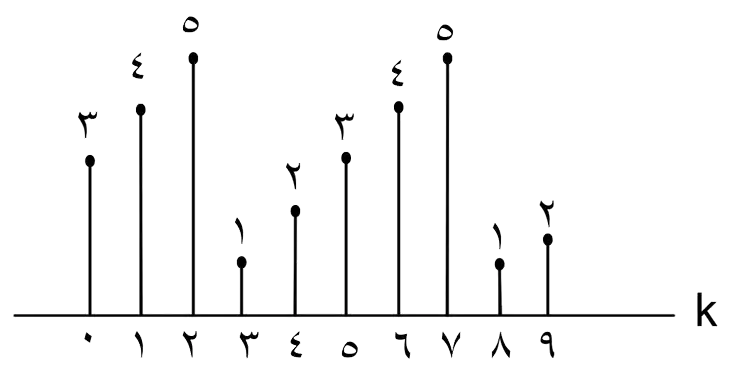
2 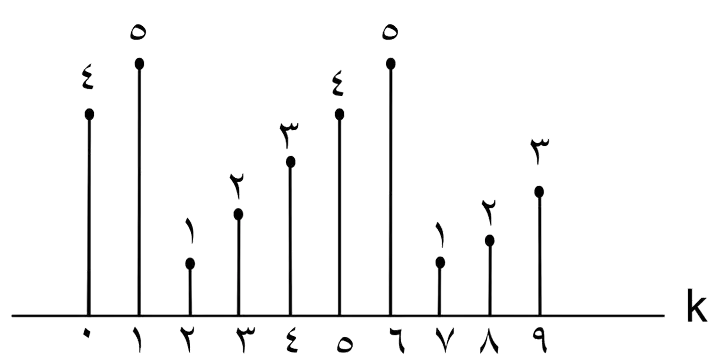
3 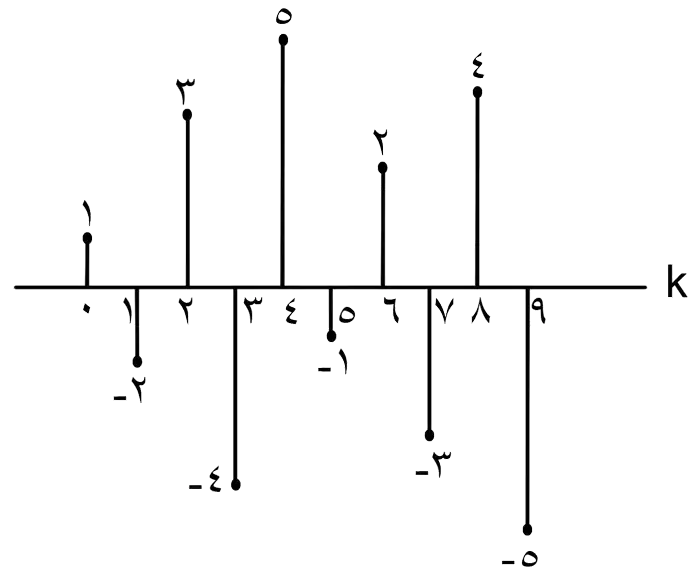
4 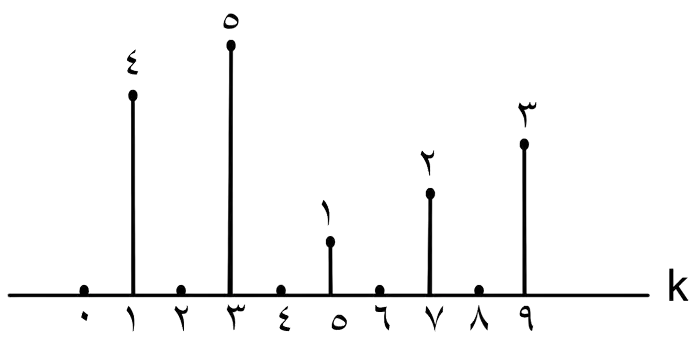
گزینه 4 صحیح است.
چون سیگنال $x[n]$ با دوره 5 متناوب است در نتیجه سری فوریه آن به صورت زیر بدست میآید:
$x\left[n\right]=\sum_{k\ =\ \lt N \gt }{a_ke^{jk{\omega }_0n}}\ \ \ {{\stackrel{{\omega }_0\ =\ \frac{2\pi }{N}\ =\ \frac{2\pi }{5}}{\Longrightarrow}}}\sum_{k\ =\ \lt N \gt }{a_ke^{j\frac{2k\pi }{5}n}}$
سوال از ما ضرایب سری فوریه $(-1)^n x[n]$ را خواسته است که میتوان آن را به شکل زیر نوشت:
${\left(-1\right)}^nx\left[n\right]=x\left[n\right]e^{j\pi n}=e^{j\pi n}\times \sum_{k\ =\ \lt N\gt }{a_ke^{j\frac{2k\pi }{5}n}}=\sum_{k\ =\ \lt N\gt }{a_ke^{j\frac{n\pi }{5}\left(2k+5\right)}}$
از طرفی با استفاده از استدلال زیر میفهمیم که سیگنال $(-1)^n x[n]$ با دورهی 10 متناوب است:
در نتیجه میتوان سیگنال $(-1)^n x[n]$ را به صورت زیر نوشت:
${\left(-1\right)}^nx\left[n\right]=\sum_{k\ =\ \lt N\gt }{b_ke^{jk{\omega }_0n}}\ \ \ {{\stackrel{{\omega }_0\ =\ \frac{2\pi }{N}\ =\ \frac{2\pi }{10}}{\Longrightarrow}}}\sum_{k\ =\ \lt N\gt }{b_ke^{j\frac{n\pi }{5}k}}$
با مقایسه دو عبارت بدست آمده برای سیگنال $(-1)^n x[n]$ میتوان با اعمال مراحل زیر روی متغیر k در ضرایب $a_k$ ، به ضرایب $b_k$ رسید:
$1) \ k \to \frac {k}{2}$
$2) \ k \to k-5$
حال اگر مراحل ذکر شده را روی شکل $a_k$ نیز اعمال کنیم، به شکل گزینهی 4 خواهیم رسید.
روش دوم: استفاده از دورههای نکته و تست درسهای کنکور کامپیوتر
دوره های نکته و تست کنکور کامپیوتر باهدف تسلط دانشجویان بر تستزنی هر درس تهیه شده است. این دورهها جواب تشریحی تمامی تستهای کنکور را شامل میشوند. برای آشنایی بیشتر با این دورهها از لینکهای زیر استفاده کنید.
پاسخ نامه کنکور ارشد کامپیوتر ۱۳۹۶
برای دسترسی به پاسخ نهایی کلیدی برای هر دفترچه کنکور میتوانید به صفحه دفترچه سوالات کنکور ارشد مهندسی کامپیوتردانلود سوالات کنکور ارشد کامپیوتر دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند مراجعه کنید. همچنین در زیر پاسخ کلیدی دفترچه کنکور کامپیوتر سال ۱۳۹۶ قرار گرفته است.
دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند مراجعه کنید. همچنین در زیر پاسخ کلیدی دفترچه کنکور کامپیوتر سال ۱۳۹۶ قرار گرفته است.
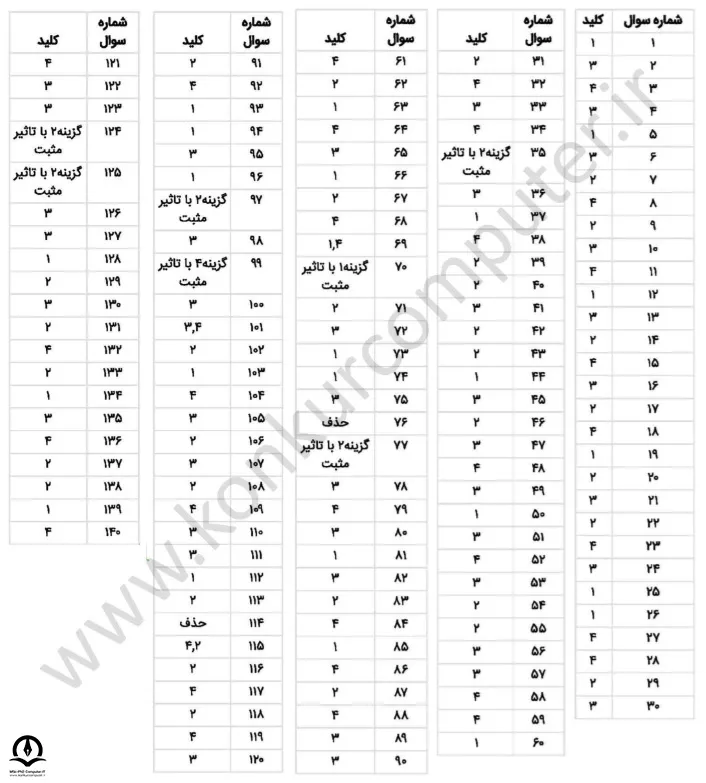
کلید کنکور ارشد کامپیوتر ۱۳۹۶
در تصویر زیر پاسخ کلیدی کنکور ارشد کامپیوتر ۱۳۹۶ آمده است. این پاسخ در واقع پاسخ کلیدی سازمان سنجش برای کنکور کامپیوتر است.
جمعبندی
داوطلبان آزمون کارشناسی ارشد کامپیوتر برای پاسخگویی به سوالات کنکور ارشد کامپیوتر نیاز به دانش عمیق و تسلط بر مباحث مورد نظر دارند و لازم است که از منابع مناسبی استفاده کنند پس استفاده از دوره نکته و تست و پلتفرم آزمون را به شما پیشنهاد میکنیم.
چگونه به پاسخ های تشریحی کنکور ارشد کامپیوتر سال ۱۳۹۶ دسترسی داشته باشیم؟
دو روش برایتان در نظر گرفته شده است: (۱) پلتفرم آزمون (۲) دورههای نکته و تست
آیا این منابع پاسخ تشریحی تستهای سالهای دیگر را شامل میشوند؟
بله. هر کدام از منابع معرفیشده پاسخ تشریحی تمامی تستهای هر درس را شامل میشود.
چگونه میتوانم بهتمامی پاسخهای کلیدی کنکور ارشد دسترسی داشته باشم؟
پاسخ کلیدی کنکورهای کامپیوتر برای تمامی سالها را میتوانید از صفحه دفترچههای کنکور کامپیوتر دانلود کنید.

اشتراکhttps://www.konkurcomputer.ir/d9b7


 این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده، پایگاه دادهدرس پایگاه داده ⚡️ پایگاه داده کنکور ارشد کامپیوتر و آی تی
این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده، پایگاه دادهدرس پایگاه داده ⚡️ پایگاه داده کنکور ارشد کامپیوتر و آی تی این مقاله عالی توضیح داده که درس پایگاه داده چیست و چه کاربردهایی دارد و منابع و سرفصل های درس پایگاه داده در آزمون کنکور ارشد کامپیوتر و آی تی را بررسی کرده
، مدار منطقیآموزش مدار منطقی به زبان ساده - بررسی مدار منطقی و انواع آن
این مقاله عالی توضیح داده که درس پایگاه داده چیست و چه کاربردهایی دارد و منابع و سرفصل های درس پایگاه داده در آزمون کنکور ارشد کامپیوتر و آی تی را بررسی کرده
، مدار منطقیآموزش مدار منطقی به زبان ساده - بررسی مدار منطقی و انواع آن امروزه درک صحیحی از مدارهای منطقی برای هر مهندس برق و کامپیوتر ضروری است. این مدارها عنصر اصلی کامپیوترها و بسیاری از وسایل الکترونیکی اطراف ما هستند، در این صفحه به بررسی و آموزش مدار منطقی پرداخته شده است و سیگنال ها و سیستم هاهمه چیز درباره درس سیگنال و سیستم، 0 تا 100 سیگنال و سیستم
امروزه درک صحیحی از مدارهای منطقی برای هر مهندس برق و کامپیوتر ضروری است. این مدارها عنصر اصلی کامپیوترها و بسیاری از وسایل الکترونیکی اطراف ما هستند، در این صفحه به بررسی و آموزش مدار منطقی پرداخته شده است و سیگنال ها و سیستم هاهمه چیز درباره درس سیگنال و سیستم، 0 تا 100 سیگنال و سیستم این صفحه به معرفی درس سیگنال و سیستم به زبان ساده پرداخته، همچنین پیش نیاز درس سیگنال و سیستم و سرفصلهای آن بررسی و منابع درس سیگنال و سیستم معرفی شده است ارائه شده است.
این صفحه به معرفی درس سیگنال و سیستم به زبان ساده پرداخته، همچنین پیش نیاز درس سیگنال و سیستم و سرفصلهای آن بررسی و منابع درس سیگنال و سیستم معرفی شده است ارائه شده است.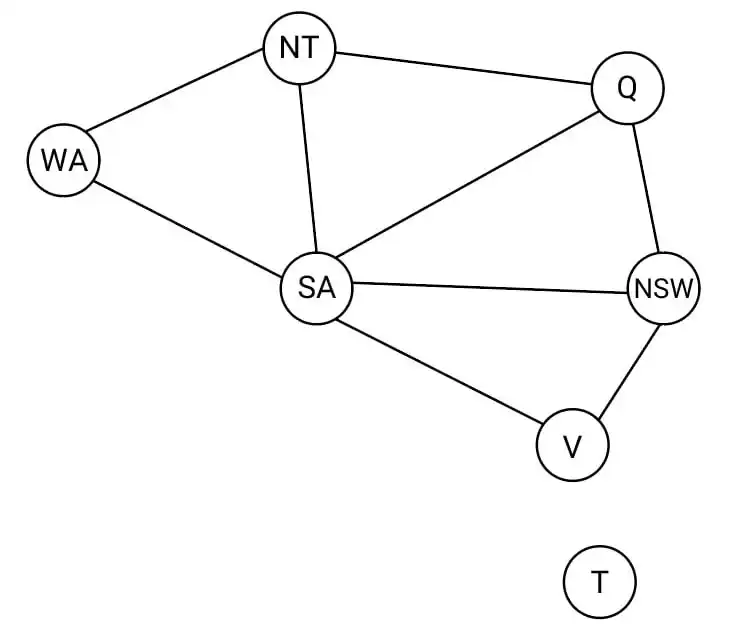







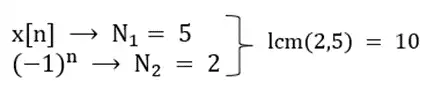
 از نگاه دانشجویان، قدرت بیان فوق العاده استاد رضوی و پوشش ۱۰۰ درصدی تمامی سرفصلها، نکات و تستها، ویدیوهای حل تست ساختمان داده و طراحی الگوریتم را به بهترین ویدیو حل تست کشور در درس ساختمان و الگوریتم تبدیل کرده است. این فیلم پرطرفدارترین و پرفروشترین فیلم حل تست ساختمان داده و الگوریتم کشور است و هر سال بیش از ۶۰۰۰ نفر این فیلم را تهیه میکنند
از نگاه دانشجویان، قدرت بیان فوق العاده استاد رضوی و پوشش ۱۰۰ درصدی تمامی سرفصلها، نکات و تستها، ویدیوهای حل تست ساختمان داده و طراحی الگوریتم را به بهترین ویدیو حل تست کشور در درس ساختمان و الگوریتم تبدیل کرده است. این فیلم پرطرفدارترین و پرفروشترین فیلم حل تست ساختمان داده و الگوریتم کشور است و هر سال بیش از ۶۰۰۰ نفر این فیلم را تهیه میکنند
 بهترین دوره نکته و تست هوش مصنوعی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست هوش و نحوه استفاده از نکته و تست هوش مصنوعی گفته شده
بهترین دوره نکته و تست هوش مصنوعی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست هوش و نحوه استفاده از نکته و تست هوش مصنوعی گفته شده
 دوره نکته و تست پایگاه داده و ویژگیها و اهمیت دوره نکته و تست پایگاه داده و نحوه استفاده صحیح از نکته و تست پایگاه داده کنکور ارشد کامپیوتر و آیتی در این صفحه عالی توضیح داده شده است
دوره نکته و تست پایگاه داده و ویژگیها و اهمیت دوره نکته و تست پایگاه داده و نحوه استفاده صحیح از نکته و تست پایگاه داده کنکور ارشد کامپیوتر و آیتی در این صفحه عالی توضیح داده شده است
 بهترین دوره نکته و تست سیستم عامل در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست سیستم های عامل و نحوه استفاده از نکته و تست سیستم عامل گفته شده
بهترین دوره نکته و تست سیستم عامل در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست سیستم های عامل و نحوه استفاده از نکته و تست سیستم عامل گفته شده
 بهترین دوره نکته و تست شبکه کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست شبکه های کامپیوتری و نحوه استفاده از نکته و تست شبکه گفته شده
بهترین دوره نکته و تست شبکه کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست شبکه های کامپیوتری و نحوه استفاده از نکته و تست شبکه گفته شده
 دوره نکته و تست نظریه زبان ها و ماشین ها در این صفحه قرار گرفته و ویژگی ها و اهمیت دوره نکته و تست نظریه زبان ها و ماشین ها بررسی شده است
دوره نکته و تست نظریه زبان ها و ماشین ها در این صفحه قرار گرفته و ویژگی ها و اهمیت دوره نکته و تست نظریه زبان ها و ماشین ها بررسی شده است
 دوره نکته و تست سیگنال و سیستم و ویژگیهای نکته و تست سیگنال و نحوه استفاده صحیح از نکته و تست سیگنال کنکور ارشد کامپیوتر در این صفحه عالی توضیح داده شده
دوره نکته و تست سیگنال و سیستم و ویژگیهای نکته و تست سیگنال و نحوه استفاده صحیح از نکته و تست سیگنال کنکور ارشد کامپیوتر در این صفحه عالی توضیح داده شده
 بهترین دوره نکته و تست مدار منطقی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست مدار منطقی و نحوه استفاده از نکته و تست مدار منطقی گفته شده
بهترین دوره نکته و تست مدار منطقی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست مدار منطقی و نحوه استفاده از نکته و تست مدار منطقی گفته شده
 بهترین دوره نکته و تست الکترونیک دیجیتال کشور در این صفحه معرفی شده و اهمیت دوره نکته و تست الکترونیک دیجیتال و نحوه استفاده صحیح از دوره بیان شده است
بهترین دوره نکته و تست الکترونیک دیجیتال کشور در این صفحه معرفی شده و اهمیت دوره نکته و تست الکترونیک دیجیتال و نحوه استفاده صحیح از دوره بیان شده است
 بهترین دوره نکته و تست ریاضیات گسسته کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست گسسته و نحوه استفاده از نکته و تست گسسته گفته شده
بهترین دوره نکته و تست ریاضیات گسسته کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست گسسته و نحوه استفاده از نکته و تست گسسته گفته شده
 دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند مراجعه کنید. همچنین در زیر پاسخ کلیدی دفترچه کنکور کامپیوتر سال ۱۳۹۶ قرار گرفته است.
دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند مراجعه کنید. همچنین در زیر پاسخ کلیدی دفترچه کنکور کامپیوتر سال ۱۳۹۶ قرار گرفته است.























































