فصل 1
سیستم نمایش اعداد
تمامی سیستمهای کامپیوتری به منظور پردازش دادهها طراحی میشوند. دادهها را میتوان بهطور کلی به دو دسته دادههای عددی (مانند اعداد ممیز ثابت) و دادههای غیرعددی (مانند کرکتر ʼAʻ) تقسیم کرد. از آنجا که در درس معماری کامپیوتر، هدف یادگیری طراحی سیستمهای کامپیوتری برای پردازش دادههای عددی است، در این بخش مروری بر روشهای مختلف نمایش دادههای عددی خواهیم داشت.
1-1 نمایش اعداد ممیز ثابت
در نمایش ممیز ثابت، نقطه ممیز در یک محل در عدد به صورت ثابت در نظر گرفته میشود و دیگر محل آن تغییر نخواهد کرد. توجه داشته باشید که نقطه ممیز در رجیستر ذخیره نمیشود و صرفاً تعبیری است که ما از عدد داریم. برای روشن شدن مطلب به مثال زیر توجه کنید:
مثال: رشته پنج بیتی \( (10100)_{2} \) را در مبنای 2 در نظر بگیرید. فرض کنید که نقطه ممیز را در سه حالت مختلف زیر در نظر گرفتهایم.
| ممیز در سمت راستترین محل: در این حالت یک عدد 5 بیتی صحیح با مقدار 20 داریم | .10100 |
| ممیز در سمت چپترین محل: در این حالت یک عدد کسری با مقدار 0.625 داریم | 10100. |
| ممیز در محلی بین دو حالت قبل: در این حالت یک عدد مرکب با مقدار 2.5 داریم | 10.100 |
همانطور که مشخص است از یک دنباله عددی ثابت بسته به جای نقطه ممیز سه مقدار عددی مختلف به دست میآید. بهطور کلی عدد ممیز ثابت N را به صورت زیر نشان میدهیم:
$$ N = (\underbrace{a_{n-1}a_{n-2}...a_{0}}_{Integral Part}.\underbrace{a_{-1}a_{-2}...a_{\partial}}_{Fractional Part})_{r} $$
که در آن r مبنا یا ریشه (Radix) عدد را نمایش میدهد و یک عدد صحیح و مثبت بزرگتر از 1 است. به هر یک از \( a_{i} \) ها یک رقم (Digit) گفته میشود. این عدد دارای یک بخش صحیح (Integral Part) با n رقم و یک بخش کسری (Fractional Part) با m رقم است. هر یک از رقمهای \( a_{i} \) یک عدد طبیعی است که در رابطه \( 0 \le a_{i} \le r - 1 \) صدق میکند.
به عبارت دیگر در مبنای r، رقمهای مجاز برای نمایش عدد بین "∘" تا 1- r قرار دارند.
مثال: اگر 10= r، سیستم نمایش دهدهی (Decimal) اعداد را خواهیم داشت که به صورت روزمره از آن استفاده میکنیم. در سیستم دهدهی، رقمهای مجاز بین "∘" تا 9 خواهد بود.
مثال: اگر 2= r، سیستم نمایش دودویی (Binary) اعداد را داریم. در این سیستم نمایش، رقمهای مجاز به صورت \( a_{i} \in \{0,1\} \) در میآید. از آنجا که در این سیستم نمایش، رقمها فقط یکی از دو مقدار "∘" و 1 را اختیار میکنند، به هر یک از این رقمها، یک رقم دودویی (Binary Digit) یا به اختصار (Bit) گفته میشود. بنابراین بیت یک رقم دودویی را نشان میدهد.
مثال: اگر 16= r، سیستم نمایش شانزده (Hexa-Decimal) اعداد را خواهیم داشت. در این سیستم نمایش، رقمهای مجاز به صورت \( a_{i} \in \{0,1,...,15\} \) در میآید. در این سیستم نمایش ممکن است در تعبیر اعداد ابهام پیش بیاید. برای مثال عدد \( 214_{16} \) را در نظر بگیرید. این عدد را میتوان به صورت یک عدد سه رقمی با رقمهای 2، 1 و 4 و یا به صورت یک عدد دو رقمی با رقمهای 2 و 14 در نظر گرفت. برای برطرف کردن این ابهام، برای نمایش رقمهای 15، 14، 13، 12، 11، 10 به ترتیب از حروف F، E، D، C، B، A استفاده میکنیم. بنابراین مجموعه رقمهای مجاز به صورت \( \{0,...,9,A,B,C,D,E,F\} \) در میآید.
تا به حال اشاره کردیم که هر عدد ممیز ثابت به صولهای از رقمها نمایش داده میشود. حال باید رابطهای را تعریف کنیم که دنبالهای از رقمها را به معادل عددی آن تبدیل کند. در سیستم نمایش سنتی اعداد برای رقم موجود در موقعیت i وزن \( r^i \) در نظر گرفته میشود:
$$ r^{n-1} r^{n-2} ... r^{0} \text{ } r^{-1}... r^{-m} $$
$$ a_{n-1} a_{n-2} ... a_{0} . a_{-1}... a_{-m} $$
برای محاسبه مقدار عددی N از رابطه زیر استفاده میکنیم:
$$ N_{V} = \lvert N \rvert = \sum_{i=-m}^{n-1} a_{i} r^{i} $$
مثال: مقدار عددی \(N = (243.1)_{5}\) را به دست آورید.
$$ N_{V} = 2\times5^2 + 4\times5^1 + 3\times5^0 + 1\times5^{-1} = 73.2 $$
مثال: مقدار عددی \(N = (1010001.01)_{2}\) را به دست آورید.
$$ N_{V} = 1\times2^6 + 0\times2^5 + 1\times2^4 + 0\times2^3 + 0\times2^2 + 0\times2^1 + 1\times2^0 + 0\times2^{-1} + 1\times2^{-2} = 81.25 $$
مثال: مقدار عددی \(N = (11100)_{2}\) را به دست آورید.
در این مثال رقمهای 1 در محلهایی به وزن 1، 8 و 16 قرار دارد، بنابراین داریم: \(N_V = 16+9+4 = 28\)
محدوده نمایش: محدوده نمایش اعداد ممیز ثابت با n رقم صحیح و m رقم کسری به صورت زیر تعریف میشود: \( 0 \le N \le r^n - r^{-m} \)
کوچکترین عدد قابل نمایش وقتی به دست میآید که تک تک رقمها برابر"∘" باشند.
بزرگترین عدد قابل نمایش وقتی است که همه رقمها 1- r باشند:
$$ (r-1)(r-1)...(r-1).(r-1)...(r-1) $$
مقدار عددی این عبارت از رابطه زیر به دست میآید:
$$ \begin{matrix} & \overbrace{100..00}^{n}.\overbrace{00..00}^{m} \\ - &\quad\quad\;\, 0.00...01\\ \end{matrix} $$
برای انجام این تفریق دقیقاً مانند تفریق عادی در مبنای 10 عمل میکنیم، یعنی در صورت نیاز به رقم قرضی از رقم قبلی غیر صفر یک واحد قرض کرده و به رقم بعدی r واحد اضافه میکنیم:
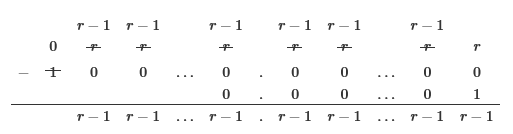
تعداد اعداد قابل نمایش: تعداد اعداد ممیز ثابت قابل نمایش با n رقم صحیح و m رقم کسری برابر \( r^{n+m} \) است.
1-2 تبدیل مبناها
برای تبدیل یک عدد از یک مبنا به یک مبنای دیگر، سه حالت مختلف را در نظر میگیریم که در این قسمت به توضیح این حالتها میپردازیم.
1-2-1 تبدیل از مبنای \( r_1 \) به مبنای 10
تبدیل یک عدد از مبنای \( r_1 \) به مبنای 10 معادل به دست آوردن مقدار عددی آن عدد است.
مثال: عدد \(N = (10100)_{2}\) را به مبنای 10 تبدیل کنید.
\[{\left(\mathrm{10100}\right)}_{\mathrm{2}}\mathrm{=}\mathrm{16}\mathrm{+}\mathrm{4}\mathrm{\ =\ }\mathrm{20}\]
بنابراین:
\[{\left(\mathrm{10100}\right)}_{\mathrm{2}}\mathrm{=}{\left(\mathrm{20}\right)}_{\mathrm{10}}\]
مثال: عدد \(N = (A60)_{16}\) را به مبنای 10 تبدیل کنید.
\[{\left(\mathrm{A}\mathrm{60}\right)}_{\mathrm{16}}\mathrm{=}\mathrm{10}\mathrm{\times }{\mathrm{16}}^{\mathrm{2}}+\mathrm{6}\mathrm{\times }{\mathrm{16}}^{\mathrm{1}}+\mathrm{\circ }\mathrm{\times }{\mathrm{16}}^{\mathrm{\circ }}=\mathrm{2656}\]
بنابراین:
\[{\left(\mathrm{A}\mathrm{60}\right)}_{\mathrm{16}}\mathrm{=}{\left(\mathrm{2656}\right)}_{\mathrm{10}}\]
1-2-2 تبدیل از مبنای 10 به مبنای \( r_2 \)
فرض میکنیم بخش صحیح و بخش کسری عدد N به ترتیب با \( N_1 \) و \( N_F \) نمایش داده شده باشد. در این صورت برای تبدیل عدد N از مبنای 10 به مبنای \( r_2 \) ، به صورت زیر عمل میکنیم:
-
برای تبدیل بخش صحیح عدد N از تقسیم متوالی به مبنای \( r_2 \) استفاده میکنیم:
$\mathrm{\circ }\mathrm{\ }\mathrm{\le }\mathrm{\ }{\mathrm{b}}_{\mathrm{i}}\le {\mathrm{r}}_{\mathrm{2}}-\mathrm{1}$${\mathrm{N}}_{\mathrm{I}}\mathrm{=}\left\{\left[\dots \left({\mathrm{b}}_{\mathrm{i}\mathrm{-}\mathrm{1}}{\mathrm{r}}_{\mathrm{2}}+{\mathrm{b}}_{\mathrm{i}\mathrm{-}\mathrm{2}}\right){\mathrm{r}}_{\mathrm{2}}+\dots +{\mathrm{b}}_{\mathrm{2}}\right]{\mathrm{r}}_{\mathrm{2}}+{\mathrm{b}}_{\mathrm{1}}\right\}{\mathrm{r}}_{\mathrm{2}}+{\mathrm{b}}_{\mathrm{\circ }}$بنابراین اگر \( N_1 \) را بر \( r_2 \) تقسیم کنیم، رقم \( b_0 \) به عنوان باقیمانده و \( \left(\dots \left({\mathrm{b}}_{\mathrm{i}\mathrm{-}\mathrm{1}}{\mathrm{r}}_{\mathrm{2}}+{\mathrm{b}}_{\mathrm{i}\mathrm{-}\mathrm{2}}\right){\mathrm{r}}_{\mathrm{2}}+\dots +{\mathrm{b}}_{\mathrm{2}}\right){\mathrm{r}}_{\mathrm{2}}\mathrm{+}{\mathrm{b}}_{\mathrm{1}} \) به عنوان خارجقسمت به دست میآید. با تقسیم خارجقسمت بر \( r_2 \) رقم \( b_1 \) به دست میآید و این کار تا وقتی به خارجقسمتی کوچکتر از \( r_2 \) برسیم، به همین شکل ادامه پیدا میکند.
-
برای تبدیل بخش کسری عدد N از ضرب متوالی در مبنای \( r_2 \) استفاده میکنیم:
$\mathrm{\circ }\mathrm{\ }\mathrm{\le }{\mathrm{b}}_{\mathrm{i}}\le {\mathrm{r}}_{\mathrm{2}}-\mathrm{1}$${\mathrm{N}}_{\mathrm{F}}\mathrm{=}{{\mathrm{r}}_{\mathrm{2}}}^{-\mathrm{1}}\left\{{\mathrm{b}}_{-\mathrm{1}}+{{\mathrm{r}}_{\mathrm{2}}}^{-\mathrm{1}}\left[{\mathrm{b}}_{-\mathrm{2}}+{{\mathrm{r}}_{\mathrm{2}}}^{-\mathrm{1}}\left({\mathrm{b}}_{-\mathrm{3}}+\dots \right)\right]\right\} $بنابراین اگر \( N_F \) را در \( r_2 \) ضرب کنیم، رقم \( b_{-1} \) به عنوان بخش صحیح حاصلضرب و \( {{\mathrm{r}}_{\mathrm{2}}}^{-\mathrm{1}}\left[{\mathrm{b}}_{-\mathrm{2}}+{{\mathrm{r}}_{\mathrm{2}}}^{-\mathrm{1}}\left({\mathrm{b}}_{-\mathrm{3}}+\dots \right)\right]\) به عنوان بخش کسری حاصلضرب به دست میآید. با ضرب بخش کسری حاصل در \( r_2 \) رقم \( b_{-2} \) به دست میآید و این کار تا "∘" شدن بخش کسری، به همین شکل ادامه پیدا میکند.
مثال: عدد \( N = (25.625)_{10} \) را به مبنای 2 تبدیل کنید.
تبدیل بخش صحیح: ابتدا عدد 25 را بر 2 تقسیم میکنیم، خارجقسمت برابر 12 و باقیمانده برابر 1 است که این باقیمانده بیت \( b_{0} \) را نشان میدهد. حال 12 را بر 2 تقسیم میکنیم، خارجقسمت برابر 6 و باقیمانده برابر "∘" است که این باقیمانده بیت \( b_{1} \) را نشان میدهد. با تقسیم 6 بر 2 خارجقسمت و باقیمانده به ترتیب برابر 3 و "∘" است که این باقیمانده بیت \( b_{2} \) را نشان میدهد. در نهایت با تقسیم 3 بر 2 به باقیمانده 1 و خارجقسمت 1 میرسیم که به ترتیب بیتهای \( b_{3} \) و \( b_{4} \) را نشان میدهد. بنابراین بخش صحیح عدد برابر است با: \( (11001)_{2} \)
تبدیل بخش کسری: ابتدا عدد 0.625 را در 2 ضرب میکنیم، که حاصل برابر 1.25 میشود. رقم صحیح به دست آمده یعنی 1 اولین بیت پس از ممیز یعنی \( b_{-1} \) را نشان میدهد. با ضرب بخش کسری یعنی 0.25 در 2، حاصل برابر 0.5 میشود که بخش صحیح یعنی "∘" بیت \( b_{-2} \) را نشان میدهد. در نهایت با ضرب بخش کسری 0.5 در 2، بیت \( b_{-3} \) برابر 1 به دست میآید. بنابراین بخش کسری عدد برابر است با: \( (0.101)_{2} \)
روابط زیر این مراحل را نشان میدهد:
| 0.625×2 = 1.25 0.25×2 = 0.5 0.5×2 = 1.0 |
 |
بنابراین داریم:
$$ (25.625)_{10} = (11001.101)_{2} $$
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096
مثال: عدد \(N = (593)_{10}\) را به مبنای 2 تبدیل کنید.
بزرگترین توان 2 که امکان کم کردن آن از عدد 593 وجود دارد عدد 512 است، سپس میتوان به ترتیب اعداد 64، 16 و 1 را از باقیمانده کم کرد (روابط زیر را ببینید).
593 - 512 = 81
81 - 64 = 17
17 - 16 = 1
1 - 1 = 0
بنابراین در معادل مبنای 2 این عدد در محلهایی به وزن 1، 16، 64 و 512 بیت 1 و در سایر محلها بیت "∘" داریم. یعنی:
$$ (593)_{10} = (1001010001)_{2} $$
مثال: برای نمایش عدد \(N = (345)_{10}\) در مبنای 2 به چند بیت نیاز داریم؟
از آنجا که \(2^8 = 256 \le 345 \lt 2^9 = 512\) برای نمایش این عدد در مبنای 2 به 9 بیت نیاز داریم.
مثال: عدد \(N = (451.5)_{10}\) را به مبنای 16 تبدیل کنید.
روابط زیر مراحل تبدیل را نشان میدهد:
| 0.5×16 = 8.0 |  |
بنابراین داریم:
$$ (451.5)_{10} = (1E3.8)_{16} $$
1-2-3 تبدیل از مبنای \( r_1 \) به مبنای \( r_2 \)
برای تبدیل یک عدد از مبنای \( r_{1} \) به مبنای \( r_{2} \) ، ابتدا عدد را از مبنای \( r_{1} \) به مبنای 10 تبدیل کرده و سپس عدد را از مبنای 10 به مبنای \( r_{2} \) تبدیل میکنیم.
مثال: عدد \(N = (23.3)_{5}\) را به مبنای 2 تبدیل کنید.
ابتدا عدد را به مبنای 10 تبدیل میکنیم:
$$ (23.3)_{5} = 2\times5^1 + 3\times5^0 + 3\times5^{-1} = (13.6)_{10} $$
حال عدد 13.6 را به مبنای 2 تبدیل میکنیم:
| 0.6×2 = 1.2 0.2×2 = 0.4 0.4×2 = 0.8 0.8×2 = 1.6 |
13 - 8 = 5 5 - 4 = 1 1 - 1 = 0 |
بنابراین داریم:
$$ (13.6)_{10} = (1101.\overline{1001})_{2} $$
مثال: فرض کنید عدد N در مبنای \( r_{1} \) با \( n_{1} \) رقم نمایش داده شده است. اگر بخواهیم این عدد را به مبنای \( r_{2} \) تبدیل کنیم، تعداد رقمهای مورد نیاز در مبنای جدید چقدر است؟
تعداد رقمهای مورد نیاز در مبنای مقصد باید به گونهای باشد که بتوان بزرگترین عدد قابل نمایش در مبنای \( r_{1} \) با \( n_{1} \) رقم را در مبنای مقصد نمایش داد. از این رو بزرگترین عدد قابل نمایش با \( n_{1} \) رقم در مبنای مبدأ باید از بزرگترین عدد قابل نمایش در مبنای مقصد کوچکتر باشد، بنابراین اگر فرض کنیم \( n_{2} \) تعداد رقمهای مورد نیاز برای نمایش عدد N در مبنای \( r_{2} \) باشد، باید رابطه \( r_{1}^{n1} - 1 \le r_{2}^{n2} -1 \) برقرار باشد.
$$ r_{1}^{n1} - 1 \le r_{2}^{n2} -1 \Rightarrow n_{1} log r_{1} \le n_{2} log r_{2} \Rightarrow n_{2} \ge n_{1} \frac{logr_{1}}{logr_{2}} \Rightarrow n_{2}\lceil n_{1}\frac{logr_{1}}{logr_{2}}\rceil $$
$$ n_{2}\lceil n_{1}\frac{logr_{1}}{logr_{2}}\rceil $$
مثال: تعداد بیتهای لازم برای نمایش یک عدد 3 رقمی دهدهی در مبنای 2 چیست؟
$$ n_{2}\lceil n_{1}\frac{logr_{1}}{logr_{2}}\rceil = \lceil 3\frac{log10}{log2}\rceil = \lceil 3\frac{1}{0.301}\rceil = 10 $$
مثال: عدد \(N = (01101001101001.010111)_{2}\) را به مبنای 16 تبدیل کنید.
از آنجا که در این مثال \( r_{1}=2 , r_{2}=2^4\) بنابراین 4 = k است.
$$ N = (\underbrace{0001}_{1} \underbrace{1010}_{A} \underbrace{0110}_{6} \underbrace{1001}_{9}.\underbrace{0101}_{5}\underbrace{1100}_{c})_{2} = (1A69.5C)_{16} $$
مثال: عدد \(N = (C41.5A)_{16}\) را به مبنای 2 تبدیل کنید.
از آنجا که در این مثال \( r_{2}=2 , r_{1}=2^4\) بنابراین 4 = k است.
$$ N = ( \underbrace{ C }_{1100} \underbrace{ 4 }_{0100} \underbrace{ 1 }_{0001} . \underbrace{ 5 }_{0101} \underbrace{ A }_{1010} )_{16} = (110001000001.0101101)_{2} $$
1-3 جمع و تفریق در مبنای r
عملیات جمع و تفریق در مبنای r دقیقاً مشابه مبنای 10 انجام میشود. به این صورت که اعداد رقم به رقم با هم جمع میشوند و در صورت ایجاد رقم نقلی آن را به طبقه بعد منتشر میکنیم. در عملیات تفریق نیز اعداد رقم به رقم از هم کم میشوند و در صورت نیاز به رقم قرضی از طبقه قبلی قرض گرفته میشود.
مثال: جمع زیر را در مبنای 16 انجام دهید.
\[ \begin{array}{c} \mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ {\left(\mathrm{2}\mathrm{\ \ \ \ \ A\ \ \ \ \ }\mathrm{5}\mathrm{\ \ \ \ \ .\ \ \ \ \ }\mathrm{6}\right)}_{\mathrm{16}}\ \ \ + \\ \begin{array}{c} \underline{{\left(\mathrm{4}\mathrm{\ \ \ \ \ }\mathrm{7}\mathrm{\ \ \ \ \ C\ \ \ \ \ .\ \ \ \ \ }\mathrm{8}\right)}_{\mathrm{16}}\ \ \ \ \ \ \ } \\ {\left(\mathrm{7}\mathrm{\ \ \ \ \ }\mathrm{2}\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ .\ \ \ \ \ E}\right)}_{\mathrm{16}}\ \ \ \ \ \ \ \end{array} \end{array} \]
مثال: جمع زیر را در مبنای 2 انجام دهید.
\[ \begin{array}{c} \mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ {\left(\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{\circ }\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{\circ }\mathrm{\ \ \ \ \ }\mathrm{\circ }\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{\circ }\mathrm{\ \ \ \ \ .\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{\circ }\right)}_{\mathrm{2}}\ \ \ \ \ + \\ \begin{array}{c} \underline{{\left(\mathrm{\circ }\mathrm{\ \ \ \ \ }\mathrm{\circ }\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ .\ \ \ \ \ }\mathrm{\circ }\mathrm{\ \ \ \ \ }\mathrm{1}\right)}_{\mathrm{2}}\ \ \ \ \ \ \ \ } \\ {\left(\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{\circ }\mathrm{\ \ \ \ \ }\mathrm{\circ }\mathrm{\ \ \ \ \ }\mathrm{\circ }\mathrm{\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ .\ \ \ \ \ }\mathrm{1}\mathrm{\ \ \ \ \ }\mathrm{1}\right)}_{\mathrm{2}}\ \ \ \ \ \ \ \ \end{array} \end{array} \]
مثال: تفریق زیر را در مبنای 16 انجام دهید.
$$ \require{enclose} \begin{matrix} & 25 & 20 & & \\ 4 & \enclose{horizontalstrike}{9} & \enclose{horizontalstrike}{4} & &\enclose{horizontalstrike}{22}\\ (5 & \enclose{horizontalstrike}{A} & \enclose{horizontalstrike}{5} & . &\enclose{horizontalstrike}{6})_{16} & - & \\ (2 & C & 8 & . & 9)_{16} \\ \hline (2 & D & C & . & D)_{16} \\ \end{matrix} $$
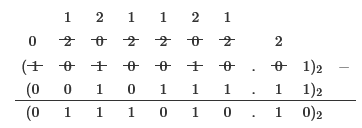
مثال: تفریق زیر را در مبنای 2 انجام دهید.