داوطلبان با استفاده از آخرین کنکورهای برگزار شده میتوانند شبیهسازی انجام دهند و عملکرد خودشان را ارزیابی کنند. دسترسی به پاسخ تشریحی این کنکورها برای مقایسه جواب دانشجو با پاسخ مرجع ضروری است. در این مقاله به روشهایی برای دسترسی به پاسخ تشریحی سوالات کنکور ارشد کامپیوتر ۱۴۰۲ اشاره خواهیم کرد.
پلتفرم آزمون کنکور کامپیوتر یک سرویس است که دانشجویان با استفاده از آن میتوانند به پاسخ تشریحی تمامی تستهای کنکور دسترسی داشته باشند، آزمون شخصیسازیشده بسازند، با دیگر دانشجویان رقابت کنند و…. برای آشنایی بیشتر با این پلتفرم پیشنهاد میکنیم از صفحه پلتفرم آزمون دیدن فرمایید.
در ادامه بهعنوان نمونهای از پاسخهای تشریحی پلتفرم آزمون، جواب تشریحی تستهای کنکور کامپیوتر ۱۴۰۲ برای درسهای ساختمان داده و طراحی الگوریتم، پایگاه داده، مدارهای منطقی و معماری کامپیوتری ارائه شده است.
تستهای درس ساختمان داده و طراحی الگوریتم کنکور کامپیوتر ۱۴۰۲ به همراه جواب تشریحی
متوسط فرض کنید برای حل یک مسئله باید از بین چهار الگوریتم انتخاب کنید. کدامیک ارجحیت دارد؟ روابط بازگشتی
1 الگوریتم A نمونهای به اندازه n را با حل بازگشتی بیست نمونه با اندازه $\frac{n}{3}$ حل میکند و سپس راهحلهای آنها را در زمان $O\left(n^2\right)$ ترکیب میکنند.
2 الگوریتم B نمونهای به اندازه n را با حل بازگشتی هشت نمونه با اندازه $\frac{n}{2}$ حل میکند و سپس راهحلهای آنها را در زمان $O\left(n^3\right)$ ترکیب میکنند.
3 الگوریتم C نمونهای به اندازه n را با حل بازگشتی دو نمونه با اندازه $2\times n$ حل میکند و سپس راهحلهاي آنها را در زمان $O\left(n\right)$ ترکیب میکنند.
4 الگوریتم D نمونهای به اندازه n را با حل بازگشتی دو نمونه با اندازه n-1 حل میکند و سپس راهحلهای آنها را در زمان ثابت ترکیب میکنند.
پیچیدگی زمانی هر روش را حساب کرده و بهترین را انتخاب میکنیم.
گزینه ۱:
$T(n)=20T(\frac{n}{3})+O(n^2 )$
با استفاده از قضیه اصلی (Master):
$n^{{{\mathrm{log}}_3 20\ }}\approx n^{2.7}\in O\left(n^{{{\mathrm{log}}_3 20\ }}\approx n^{2.7}\right)>O\left(n^2\right)\to T\left(n\right)\in O\left(n^{{{\mathrm{log}}_3 20\ }}\approx n^{2.7}\right)$
گزینه ۲:
$T\left(n\right)=8T\left(\frac{n}{2}\right)+O\left(n^3\right)$
با استفاده از قضیه اصلی (Master):
$n^{{{\mathrm{log}}_2 8\ }}=n^3\in O\left(n^3\right)\to T\left(n\right)\in O(n^3{\mathrm{log} \left(n\right)\ })$
گزینه ۳:
$T\left(n\right)=2T\left(2n\right)+O\left(n\right)$
این راهحل به جواب نمیرسد، زیرا در هر مرحله به ازای هر تعداد ورودی اولیه تعداد ورودیها در هر مرحله افزایش یافته و تا بینهایت ادامه مییابد، وچون زمان با تعداد ورودیها رابطه مستقیم دارد زمان حل مسئله به بینهایت میرود و حل ناممکن است.
گزینه ۴:
$T(n)=2T(n-1)+O(1)$
$T(n)=4T(n-2)+3×O(1)$
$T(n)=8T(n-3)+7×O(1)$
:
$T(n)=2^n T(0)+(1+2+2^2+⋯+2^{n-1} )×O(1)$
$→T(n)=(1+2+2^2+⋯+2^{n-1} )×O(1)=\frac{1(1-2^n )}{1-2}×O(1)=(2^n-1)×O(1)=2^n×O(1)=O(2^n )$
$→T(n)∈O(2^n)$
به روش سادهتر میتوان با نکته زیر مرتبه زمانی را محاسبه کرد.
نکته: مرتبه روابط بازگشتی به فرم $T(n)=aT(n-b)+c$ که در آن a, b, c اعداد ثابت هستند به صورت زیر بدست میآید:
$T\left(n\right)=\left\{ \begin{array}{c} O\left(a^{\frac{n}{b}}\right)\ \ \ \ \ :a>1 \\ O\left(n\right)\ \ \ \ \ :a=1,\ c\neq 0 \\ O\left(1\right)\ \ \ \ \ :a=1,\ c=0 \end{array} \right.$
$a=2,\ b=1,\ c=1\to T\left(n\right)=O(2^{\frac{n}{1}})$
مقایسه پیچیدگی زمانی گزینهها:
$O\left(2^n\right)>O\left(n^3{\mathrm{log} \left(n\right)\ }\right)>O\left(n^{{{\mathrm{log}}_3 20\ }}\approx n^{2.7}\right)\to \mathrm{\ \text{گزینه1}}$
یادآوری قضیه اصلی (Master):
برای رابطه بازگشتی $T\left(n\right)=aT\left(\frac{n}{b}\right)+f(n)$ که در آن a, b ثابت بوده و $a≥1,b>1$ است، قضیه اصلی دارای سه حالت گوناگون زیر است که برای حل هر مسئله یکی از این سه حالت انتخاب میشود:
حالت اول: اگر معادله $f\left(n\right)=O(n^{{{\mathrm{log}}_b a-\epsilon \ }})$ برای $ϵ>0$ برقرار باشد، آنگاه زمان زیر برای رابطه برقرار است:
$T\left(n\right)=\theta (n^{{{\mathrm{log}}_b a\ }})$
حالت دوم: اگر معادله $f\left(n\right)=\theta (n^{{{\mathrm{log}}_b a\ }})$ برقرار باشد، آنگاه زمان زیر برای رابطه برقرار است:
$T\left(n\right)=\theta (n^{{{\mathrm{log}}_b a\ }})$
حالت سوم: اگر معادله $f\left(n\right)=\mathrm{\Omega }(n^{{{\mathrm{log}}_b a-\epsilon \ }})$ برای $ϵ>0$ و اگر $af\left(\frac{n}{b}\right)\le cf(n)$ برای $c<1$ و n های بزرگ برقرار باشند، آنگاه زمان زیر برای رابطه برقرار است:
$T\left(n\right)=\theta (f\left(n\right))$
متوسط فرض کنید $A=\left[a_1,a_2,\ldots,a_n\right]$ آرایهای از اعداد صحیح متمایز باشد و k یک عدد صحیح داده شده باشد. هدف این است که دو عدد متمایز از A را پیدا کند که مجموع آنها دقیقاً k باشد، یا گزارش دهید که چنین عناصری وجود ندارد. یک الگوریتم کارا برای حل این مسئله چه زمانی خواهد داشت؟ سوالات ترکیبی
1 $O\left(\log{n}\right)$
2 $O\left(n\right)$
3 $O\left(n\log{n}\right)$
4 $O\left(n^2\right)$
روش اول: (روش مرتب کردن و استفاده از دو اشارهگر)
- مرتب کردن آرایه به صورت صعودی (آرایه مرتب شده $A'$). $O(nlog(n))$
- استفاده از دو اشارهگر p, q در آرای مرتب شده. یکی به ابتدای آرایه (p) و دیگری به انتهای آن (q) اشاره میکند. $O(1)$
- اجرای حلقه زیر: ($O(n)$)
while $q > p$ :
If $(A' [p]+A' [q]==k)$
return $A' [p],A' [q]$
else
{
if ( $ A' [p]+A' [q]
$p=p+1$
else
$p=p-1$
}
- اگر حلقه بالا به جواب نرسد، مسئله جواب ندارد بنابراین گزارش آن ارسال میشود. $O(1)$
پیچیدگی زمانی:
$O(nlog(n))+O(1)+O(n)+O(1)∈O(nlog(n))$
روش دوم: (روش مرتب کردن و جستوجوی دودویی (باینری))
- مرتب کردن آرایه به صورت صعودی (آرایه مرتب شده $A'$). $O(nlog(n))$
- گردش در تمام المانهای آرایه جدید و تلاش برای یافتن عدد $k-a$ (a عدد فعلی اشاره شده) با استفاده از الگوریتم جستوجوی دودویی. اگر به ازای عددی جستوجو موفقیتآمیز بود، دو عدد به عنوان جواب مسئله بازگردانده میشوند. $O(nlog(n))$
- در صورت نیافتن دو عدد، گزارش عدم موفقیت. $O(1)$
پیچیدگی زمانی:
$O(nlog(n))+O(nlog(n))+O(1)∈O(nlog(n))$
نکته: مرتبه زمانی الگوریتم جستوجوی دودویی (باینری) برابر با $θ(log(n))$ است.
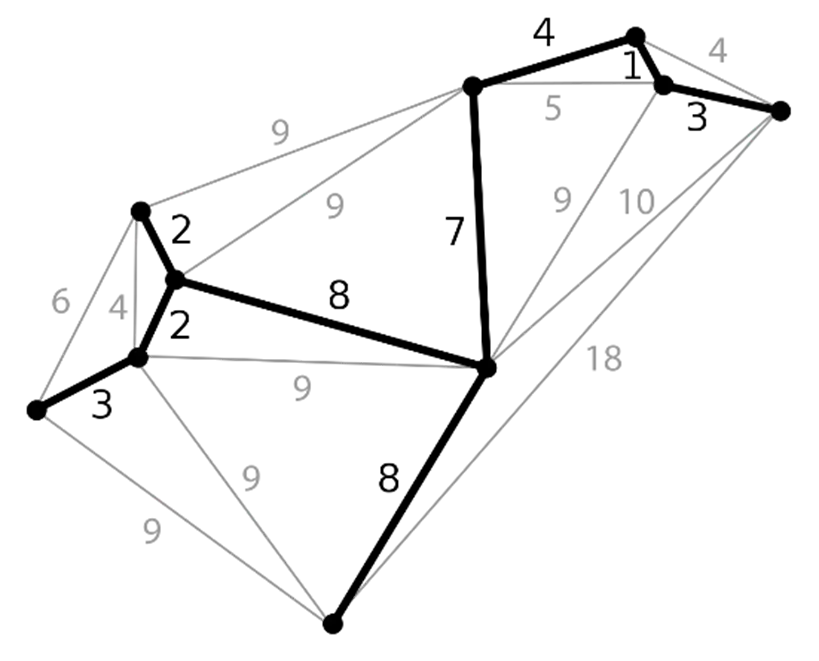
دشوار الگوریتم مرتبسازی ادغام (Mergesort) را درنظر بگیرید. بهجای اینکه آرایه ورودی را به دو قسمت تقریباً مساوی تقسیم کنیم، آنرا به m بخش تقسیم میکنیم که لزوماً مساوی نیستند (m یک ثابت است.) سپس بهصورت بازگشتی الگوریتم ادغام اصلاح شده را روی هر قسمت اجرا میکنیم و m آرایه مرتبشده را ادغام میکنیم. زمان اجرای الگوریتم ادغام اصلاح شده در حالتی که $m\gt2$ کدام است؟ مرتبسازی
1 $O\left(mn\right)$
2 $O\left(m\log{n}\right)$
3 $O\left(\log{\log{n}}\right)$
4 $O\left(n\log{n}\right)$
گزینه 4 صحیح است.
$\frac{n}{K_1}+\frac{n}{K_2}+\ldots+\frac{n}{K_m}=n\Rightarrow n\left(\frac{1}{K_1}+\frac{1}{K_2}+\ldots+\frac{1}{K_m}\right)=n\Rightarrow\frac{1}{K_1}+\frac{1}{K_2}+\ldots+\frac{1}{K_m}=1$
n عنصر
$\overbrace{}$ |
| $\frac{n}{K_m} $ |
$\frac{n}{K_2}$ |
... |
$\frac{n}{K_1}$ |
حالا روی هریک از قسمتهای $\frac{n}{K_i}$ الگوریتم مرتبسازی ادغامی را بهصورت بازگشتی فراخوانی میکنیم و درنهایت که مرتب شدند پاسخها را باهم ادغام (merge) میکنیم بنابراین زمان اجرا برابر است با:
| $T\left(m\right)=T\left(\frac{n}{K_1}\right)+T\left(\frac{n}{K_2}\right)+\ldots+T\left(\frac{n}{K_m}\right)+θ(n)∈θ(nlogn)$ |
| $\downarrow$ |
| زمان Merge |
طبق نکاتی که در مورد حل روابط بازگشتی بلد هستیم چون مجموع ضرایب n درون 4T برابر 1 شده $(\frac{1}{K_1}+\frac{1}{K_2}+\ldots+\frac{1}{K_m}=1)$ و در انتهای رابطه بازگشتی هم $\theta\left(n\right)$ داریم، مرتبه $T\left(n\right)$ برابر $\theta\left(n\log{n}\right)$ است.
متوسط کدامیک از روابط بازگشتی زیر را نمیتوان مستقیماً با قضیه اصلی حل کرد؟ روابط بازگشتی
1 $T\left(n\right)=16T\left(\frac{n}{4}\right)+n$
2 $T\left(n\right)=T\left(\frac{n}{5}\right)+20$
3 $T\left(n\right)=3T\left(\frac{n}{4}\right)+n\log{n}$
4 $T\left(n\right)=2T\left(\frac{n}{2}\right)+n\log{n}$
گزینه 4 صحیح است.
برای حل این سوال نباید از روشهای ابتکاری که برای حل روابط بازگشتی به این فرم وجود دارد استفاده کنید و فقط باید قضیه Master ساده را درنظر بگیرید.
در رابطه بازگشتی $T\left(n\right)=aT\left(\frac{n}{b}\right)+f\left(n\right)$ اگر در حاصل تقسیم $f\left(n\right)$ بر $n^{\log_b{a}}$ یا بالعکس فقط لگاریتم n مشاهده کنیم (حالا با هر توانی = $\log^K{n}$) قضیه Master جواب نمیدهد. توجه کنید که اگر $\log^K{n}$ در یک n ای ضرب بشود، قضیه Master جواب میدهد. بررسی گزینه 1) $\frac{n^{\log_4{16}}}{n}=\frac{n^2}{n}=n$ : لگاریتم تنها نشد پس Master جواب میدهد بررسی گزینه 2) $\frac{n^{\log_5{1}}}{20}=\frac{n^0}{20}=\frac{1}{20}$ : لگاریتم تنها نشد پس Master جواب میدهد. بررسی گزینه 3) $\frac{n\log{n}}{n^{\log_4{3}}}=\frac{n\log{n}}{n^{0.8}}=n^{0.2}\log{n}$ : در اینجا $f\left(n\right)$ را بر $n^{\log_b{a}}$ تقسیم کردیم، چون با این مقادیر این کار راحتتر است، توجه کنید که تفاوتی ندارد که $f\left(n\right)$ را بر $n^{\log_b{a}}$ تقسیم کنیم یا بالعکس لگاریتم تنها نشد پس Master جواب میدهد. بررسی گزینه 4) $\frac{n\log{n}}{n^{\log_2{2}}}=\frac{n\log{n}}{n}=\log{n}$ : لگاریتم تنها نشد پس Master جواب نمیدهد.
تستهای درس پایگاه داده کنکور کامپیوتر ۱۴۰۲ به همراه جواب تشریحی
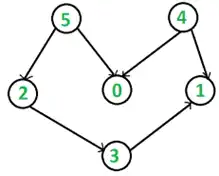
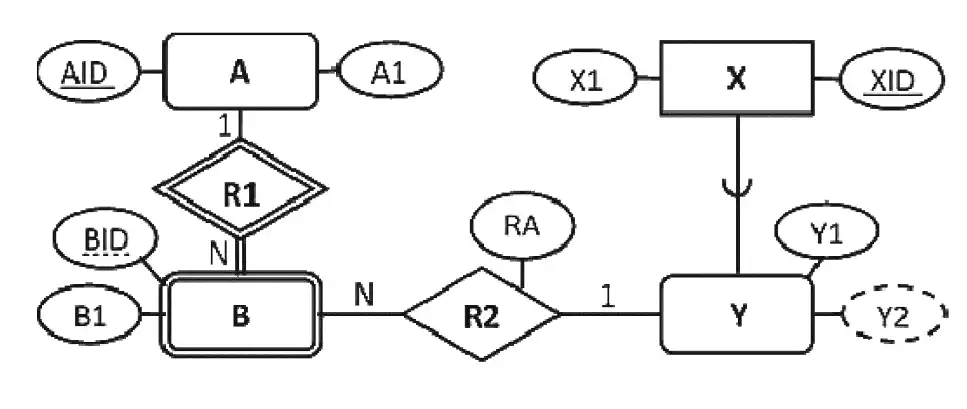
آسان کدام مورد یک طراحی منطقی درست برای نمودار EER زیر است؟
[توجه: در نمودار EER، از خط ممتد در زیر صفت برای نمایش کلید کاندیدا و از خطچین زیر صفت برای نمایش صفت ممیزه یا کلید جزئی موجودیت ضعیف استفاده شده است. در طراحی جداول، از خط ممتد در زیر صفت(ها) برای نمایش کلید اصلی و از خطچین برای نمایش کلید خارجی استفاده شده است.]
طراحی پایگاه داده
1 A(AID, A1) X(XID, X1)
B(AID, BID, B1, XID, RA) Y(XID, Y1)
2 A(AID, A1) X(XID, X1)
B(AID, BID, B1) Y(XID, AID, BID, Y1, Y2, RA)
3 A(AID, A1) X(XID, X1)
B(BID, B1, XID, RA) Y(XID, Y1)
4 A(AID, A1) X(XID, X1)
B(AID, BID, B1) Y(XID, Y1) R2(AID, BID, XID, RA)
از موجودیت A شروع میکنیم:
A یک موجودیت ساده است، موجودیتهای ساده برای خود یک رابطه تشکیل میدهند و تمام صفات ساده خود را شامل میشوند. A صفت AID را به عنوان کلید اصلی میگیرد (چون روی شکل تنها کلید کاندید است.).
A(AID, A1)
در موجودیت B:
B یک موجودیت ضعیف است، موجودیتهای ضعیف برای خود یک رابطه دارند که کلید این رابطه ترکیبی از کلید اصلی موجودیتی که به آن وابسته هستند و کلید جزئی خود میباشد. بنابراین کلید B ترکیب AID, BID میشود. صفت B1 متعلق به این موجودیت است برای همین در رابطه آن قرار میگیرد.
B در یک ارتباط N:1 با موجودیت Y قرار دارد، در اینگونه ارتباطها صفات و کلید اصلی طرف ۱ ارتباط در رابطه طرف N قرار میگیرند. بنابراین در اینجا RA به عنوان یک صفت دیگر B قرار میگیرد و کلید Y که در ادامه مشخص میشود برابر XID است، به عنوان کلید خارجی در رابطه B قرار میگیرد.
B(AID, BID, B1, XID, RA)
موجودیتهای X و Y:
موجودیت Y یک subclass بوده که superclass Xآن است. در نگاشت generalizationها و specializationها از EER به مدل رابطهای چندین روش وجود دارد:
۱- برای هر یک از subclassها و superclass یک رابطه درست کنیم، رابطه superclass شامل تنها صفات خود میباشد و subclassها علاوه بر صفات خود کلید اصلی superclass را نیز به عنوان کلید اصلی خود دارند.
۲- تنها برای هر یک از subclassها رابطه تشکیل دهیم، در اینجا هر رابطه subclass شامل صفات خود و صفات موجود متناظرش در superclass است و کلید این رابطه کلید اصلی superclass میباشد. این روش زمانی میتواند به کار رود که subclassها به صورت disjoint یعنی جدا از هم باشند. در موارد overlap کارایی ندارد.
علاوهبر دو روش بالا دو روش دیگر هم وجود دارند که به جای ایجاد چندین رابطه تنها یک رابطه ایجاد میکنند و تمام صفات superclass و subclassها را در آن قرار میدهند. (توضیحات این دو روش خارج از محدوده کنکور است.)
حال اگر به گزینهها دقت کنید هم برای X و هم برای Y رابطه تشکیل شده است بنابراین اینجا از روش ۱ استفاده شده است.
موجودیت X تمام صفات خود را دارد و XID چون تنها کلید کاندید است به عنوان کلید اصلی استفاده میشود:
X(XID, X1)
موجودیت Y تمام صفات خود را دارد و از XID که کلید X است به عنوان کلید استفاده میکند. در شکل نشان داده شده که Y صفت Y2 را نیز دارد امّا اگر دقت کنید این صفت از نوع صفت مشتق است و صفتهای مشتق در مدل رابطهای وارد نمیشوند. بنابراین در نهایت مدل رابطهای Y به صورت زیر میشود:
Y(XID, Y1)
متوسط جداول زیر برای یک باشگاه قایقسواری طراحی شده است که در آن قایقهای فراهمشده توسط تعدادی از شرکتها به اعضای باشگاه اجاره داده میشوند.
پایگاه داده رابطهای
Member (MID, MName, MDate, MType) اطلاعات اعضا شامل شمارۀ عضویت، نام، تاریخ عضویت، نوع عضویت
Boat (BID, Capacity, BType, Company) اطلاعات قایقها شامل شمارۀ قایق، ظرفیت، نوع، شرکت
Rent (MID, BID, Date, Duration) اطلاعات اجاره قایق شامل شماره عضو، شماره قایق، تاریخ اجاره، مدت اجاره به ساعت
کدام مورد، جبر رابطهای معادل شماره اعضایی است که همه قایقهای از نوع Jet، شرکت Yamaha را برای حداقل 2 ساعت متوالی اجاره کردهاند؟
1 $\Pi_{\lt MID \gt}\left(\sigma_{(Duration>=2\ AND\ Company\ =\ ’ Yamaha’ \ AND\ BType\ =\ ’ Jet ’)}\left(Rent\bowtie B o a t\right)\right)$
2 $\Pi_{\lt MID,\ BID>}\left(\sigma_{(Duration>=2)}\left(Rent\right)\right)\div\Pi_{\lt BID \gt}\left(\sigma_{(Company\ =\ ' Y a m a h a'\ AND\ BType\ =\ ' J e t')}\left(Boat\right)\right)$
3 $\Pi_{\lt MID \gt}\left(\sigma_{(Duration>=2)}\left(Rent\right)\right)-\Pi_{\lt MID \gt}\left(\sigma_{(Company\ !=\ ' Y a m a h a'\ OR\ BType\ !=\ ' J e t')}\left(Rent\bowtie B o a t\right)\right)$
4 $\Pi_{\lt MID \gt}\left(\sigma_{(Duration>=2)}\left(Member\bowtie R e n t\right)\right)\cap\Pi_{\lt MID \gt}\left(\sigma_{(Company\ =\ ' Y a m a h a'\ AND\ BType\ =\ ' J e t')}\left(Rent\bowtie B o a t\right)\right)$
بررسی گزینهها:
گزینه ۱:
$\prod_{}(\sigma_{(Duration \ge 2\ AND\ Company='Yamaha'\ AND\ BType='Jet')}(Rent\ \Join \ Boat))$
این گزینه شماره عضویت افرادی را برمیگرداند که یکی از قایقهای Jet شرکت Yamaha را به مدت بیش از ۲ ساعت اجاره کردهاند. این گزینه میتواند از هر شماره عضویت چندین نمونه داشته باشد که تعدادشان برابر تعداد قایقها و دفعات اجاره آنها توسط یک فرد میباشند.
سؤال از ما شماره عضویت افرادی که تمام قایقها را اجاره کردهاند میخواهد بنابراین این گزینه غلط است.
گزینه ۲:
$\prod_{}(\sigma_{(Duration \ge 2)}(Rent)) \div \prod _{}(\sigma_{(Company='Yamaha'\ AND\ BType='Jet')}( Boat))$
عبارت $\prod_{}{({\sigma }_{Duration\ge 2}(Rent))}$ شماره قایق و شماره عضویت مربوط به اطلاعات تمام اجارههایی که مدتشان بیش از ۲ ساعت هستند را برمیگرداند.
عبارت $\prod_{}{({\sigma }_{Company='Yamaha'AND\ BType='Jet'}\left(Boat\right))}$ شماره تمام قایقهایی را برمیگرداند که از نوع Jet شرکت Yamaha باشند.
حال تقسیم عبارت اول بر دوم شماره عضویت کسانی را برمیگرداند که تمام BIDها را شامل شده باشند. به عبارتی دیگر شماره عضویت کسانی برگردانده میشود که تمام قایقهای از نوع Jet شرکت Yamaha را اجاره کرده باشند، همچنین با توجه به رابطه اول این افراد همگی قایقها را به مدت بیش از ۲ ساعت اجاره کردهاند.
این گزینه صحیح است.
گزینه ۳:
$\prod_{}(\sigma_{(Duration \ge 2)}\ (Rent))-\prod_{}\ (\sigma_{Company!='Yamaha'\ OR \ BType!='Jet')}(Rent\ \Join \ Boat))$
عبارت $\prod_{}{({\sigma }_{Duration\ge 2}\left(Rent\right))}$ شماره عضویت افرادی را بازمیگرداند که هر قایقی را به مدت دو ساعت اجاره کرده باشند.
عبارت $\prod_{}{\left({\sigma }_{Compan!='Yamaha'OR\ BType!='Jet'}\left(Rent\infty Boat\right)\right)}$ شماره عضویت کسانی را بازمیگرداند که قایقهایی که از نوع Jet و یا از شرکت Yamaha نباشند را اجاره کردهاند.
تفریق رابطه دوم از رابطه اوّل شماره عضویت کسانی را برمیگرداند که به هیچ عنوان قایقی غیر از نوع Jet شرکت Yamaha به مدت بیش از ۲ ساعت اجاره نکرده باشند. یعنی ممکن است کسی باشد که تنها یک قایق از این نوع اجاره کرده باشد و در جواب نهایی بیاید و یا ممکن کسی باشد که تمام قایقها از جمله قایقهای خواسته سؤال را اجاره کرده باشد ولی در جواب نهایی نیاید. بنابراین این گزینه غلط است.
گزینه ۴:
$\prod_{}(\sigma_{(Duration \ge 2)}\ (Member \Join \ Rent))\cap \prod_{}\ (\sigma_{Company='Yamaha'\ AND \ BType='Jet')}(Rent\ \Join \ Boat))$
عبارت $\prod_{}{({\sigma }_{Duration\ge 2}\left(Member\infty Rent\right))}$ شماره عضویت افرادی که قایق به مدت بیش از دو ساعت اجاره کرده باشند برمیگرداند.
عبارت $\prod_{}{({\sigma }_{Company='Yamaha'\ AND\ BType='Jet'}\left(Rent\infty Boat\right))}$ شماره عضویت افرادی که قایق از نوع Jet شرکت Yamaha را اجاره کرده باشند برمیگرداند.
اشتراک دو عبارت بالا شماره عضویت افرادی که یک یا چند قایق Jet شرکت Yamaha را به مدت ۲ ساعت و یا بیشتر اجاره کرده باشند برمیگرداند. نتیجه مشابه با گزینه ۱ است. این گزینه نیز غلط است.
متوسط یک سیستم مدیریت کتابخانه براساس جداول زیر طراحی شده است.
زبان و پرس و جوی SQL
Member (MemID, Name, Age, MemType) اطلاعات اعضا شامل شناسه، نام، سن، نوع عضویت
Book (ISBN, Title, Author, Publisher) اطلاعات کتاب شامل کد شابک، عنوان، نویسنده، ناشر
Borrowed (MemID, ISBN, BorrowDate, ReturnDate) ،اطلاعات امانتگیری شامل شناسه عضو، شابک
تاریخ امانتگیری، تاریخ بازگشت
کدام مورد، این محدودیت که «هر فرد با نوع عضویت عادی (Regular) نمیتواند بیش از 2 بار یک کتاب را به امانت ببرد» را با استفاده از اظهار (Assertion) بهدرستی توصیف مینماید؟
1 $\begin{matrix}\mathrm{Create\ Assertion\ BookConstraint\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\\\mathrm{Check\ (Not\ Exists(select\ *\ from\ Member\ where\ MemType\ =\ 'Regular'\ And\ Exists\ \ \ \ \ }\\\mathrm{(Select\ *\ From\ Borrowed\ As\ B1\ Where\ Exists\ \ \ \ \ }\\\mathrm{ (select\ *\ From\ Borrowed\ As\ B2\ Where\ B1.ISBN\ =\ B2.ISBN}\\\mathrm{And\ B1.BorrowDate\ !=\ B2.BorrowDate)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\\\end{matrix}$
2 $\begin{matrix}\mathrm{Create\ Assertion\ BookConstraint\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\\\mathrm{Check\ (Not\ Exists(Select\ ISBN\ From\ Book\ Where\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\\\mathrm{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (select\ count(*)\ From\ Borrowed\ Natural\ Join\ Member\ \ \ \ \ \ \ \ \ }\\\mathrm{where\ MemType\ =\ 'regular')\ >\ 2))\ \ \ \ }\\\end{matrix}$
3 $\begin{matrix}\mathrm{Create\ Assertion\ BookConstraint\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\\\mathrm{Check\ (Not\ Exists(select\ *\ from\ Member\ where\ MemType\ =\ 'regular'\ And\ Not\ Exists}\\\mathrm{ \ \ \ \ (select\ *\ from\ Borrowed\ where\ Member.MemID\ =\ Borrowed.MemID}\\\mathrm{Group\ By\ ISBN\ Having\ count(*)\ >\ 2)))\ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\\\end{matrix}$
4 $\begin{matrix}\mathrm{Create\ Assertion\ BookConstraint\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\\\mathrm{Check\ (Not\ Exists(select\ *\ from\ Member\ Natural\ Join\ Borrowed\ Natural\ Join\ Book\ \ \ \ }\\\mathrm{where\ MemType\ =\ 'regular'\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\\\mathrm{Group\ By\ ISBN,\ MemID\ Having\ count(*)\ >\ 2))\ \ \ }\\\end{matrix}$
گزینه 4 با تاثیر مثبت توسط سنجش اعلام شد. بررسی گزینهها:
گزینه ۱:
در اینجا دو شرط لازم است True باشند تا محدودیت اعمال شده عمل کند.
۱- عضوی از نوع ‘Regular’ داشته باشیم
۲- با توجه به عبارات پرانتز سوم و دستور Exists قبل از آن، زمانی شرط دوم برقرار است که کتابی با ISBN مشخص در دو تاریخ متفاوت قرض گرفته شده باشد. اینکه کتاب توسط یکنفر یا چند نفر متفاوت قرض گرفته شده باشد و یا نوع عضویت افراد Regular بوده باشد در اینجا چک نمیشود.
بنابراین این گزینه غلط است.
به عنوان مثال: اگر دو شخص متفاوت که هر دو از نوع Regular هم هستند، کتاب یکسانی را در دو تاریخ متفاوت فقط برای یکبار قرض گرفته باشند، سیستم خطا اعلام میکند و محدودیت اعمال میشود.
گزینه ۲:
دستور Select ISBN From Book … میگوید ISBN تمام کتابهای جدول Book را برگردان اگر شرط زیر برقرار باشد. علت اینکه تمام کتابها برگردانده میشود این است که در شرط آمده مقادیر رکوردهای Book تأثیری روی شرط ندارند. در کل به دلیل دستور Not Exists اگر شرط زیر برقرار باشد محدودیت عمل میکند و سیستم خطای Assertion میدهد.
شرط (select count(*) …) > 2 میگوید بررسی کن اگر کتابی توسط فرد یکسان با نوع Regular بیش از دو بار در تاریخ یکسان و برگشت یکسان قرض گرفته شدهاست عبارت True را برگردان. به عبارتی این شرط بررسی میکند که آیا بیش از دو رکورد کاملا مشابه در جداول وجود دارد یا خیر.
برای مثال: اگر فردی با نوع عضویت Regular یک کتاب را در بیش از دو تاریخ قرض گرفته باشد این محدودیت عمل نمیکند.
گزینه ۳:
این گزینه میتوانست کاملا درست باشد اگر به جای Not Exists پس از عبارت MemType=’rgular’ And از دستور Exists استفاده شده بود.
در این گزینه ابتدا چک میشود که عضو داده شده از نوع Regular باشد سپس این عضو یک کتاب با ISBN مشخص را بیش از دو بار قرض نگرفته باشد. (در حالیکه ما اعضایی را میخواهیم که قرض گرفته باشند.)
گزینه ۴:
این گزینه دقیقا خواسته مسئله میباشد.
عبارات جلوی Not Exists شماره کتاب و عضوهایی را برمیگرداند که عضو داده شده از نوع Regular باشد و آن شخص کتابی با ISBN مشخص را بیش از دو بار قرض گرفته باشد.
آسان در رابطه R(A, B, C, D, E) با وجود وابستگی تابعی $\left(C,D\right)\rightarrow E$، کدامیک از تجزیههای زیر برای این رابطه، یک تجزیه بیکاست (Lossless, Nonless) است؟ طراحی پایگاه داده
1 $\begin{matrix}\mathrm{R}_\mathrm{1}(A,\ B,\ C,\ D)\\\mathrm{R}_\mathrm{2}\left(\mathrm{D,\ E}\right)\ \ \ \ \ \ \ \ \ \\\end{matrix}$
2 $\begin{matrix}\mathrm{R}_\mathrm{1}(A,\ B,\ D)\ \ \ \ \ \\\mathrm{R}_\mathrm{2}\left(\mathrm{A,\ B,\ C,\ E}\right)\\\end{matrix}$
3 $\begin{matrix}\mathrm{R}_\mathrm{1}(A,\ B,\ C,\ D)\ \\\mathrm{R}_\mathrm{2}\left(\mathrm{A,\ C,\ D,\ E}\right)\\\end{matrix}$
4 $\begin{matrix}\mathrm{R}_\mathrm{1}(A,\ B)\ \ \ \ \ \\\mathrm{R}_\mathrm{2}\left(\mathrm{C,\ D,\ E}\right)\\\end{matrix}$
سنجش این سوال را از کلید نهایی حذف کرد.
شرط تجزیه بیکاست یک رابطه R به چندین رابطه $R_1, R_2, \dots , R_n$ این است که پیوند طبیعی تمام این رابطهها دقیقا رابطه R را ایجاد کنند.
اگر رابطه R به دو رابطه تجزیه شود این تجزیه زمانی بیکاست است که صفت یا صفتهایی مشترک در دو رابطه وجود داشته باشند که این صفت یا صفتها حداقل در یکی از دو رابطه کلید کاندید یا سوپرکلید باشد.
به عبارت دیگر باید یکی از دو عبارت زیر برقرار باشند:
$R_1\cap R_2\to (R_1-R_2)\ or\ R_1\cap R_2\to (R_2-R_1)$
بررسی گزینهها:
گزینه ۱:
اشتراک دو رابطه صفت D است، این صفت با توجه به وابستگی تابعی داده شده نمیتواند کلید هیچکدام از دو رابطه باشد.
$D\to \left(A,\ B,\ C\right)$$\ Flase$$,\ \ \ \ \ \ D\to \left(E\right)$$\ False$
گزینه ۲:
اشتراک دو رابطه دو صفت (A, B) است، این صفتها با توجه به وابستگی تابعی داده شده نمیتوانند سوپرکلید هیچکدام از دو رابطه باشد.
$\left(A,\ B\right)\to \left(D\right)$$\ False$$,\ \ \ \ \ \ \left(A,\ B\right)\to \left(\ C,\ E\right)$$\ False$
گزینه ۳:
اشتراک دو رابطه سه صفت (C, D) است، این صفتها با توجه به وابستگی تابعی داده شده میتوانند کلید رابطه دوم باشند:
$\left(C,\ D\right)\to E$
$\Rightarrow \left(A,\ C,\ D\right)\to AE \Rightarrow \left(A,\ C,\ D\right)\to E$
$\Rightarrow \left(A,\ C,\ D\right)=R_1\cap R_2\to R_2-R_1=E$$\ \ True$
گزینه ۴:
اشتراک دو رابطه هیچ صفتی نمیشود. این گزینه مشخصاً غلط است.
دشوار چند عبارت از عبارات زیر درست است؟
اصول و مفاهیم پایه
• زبان سطح پایین دستکاری دادهها (Low Level DML) باید در یک زبان برنامه همه منظوره (General Purpose Language) نهفته شود.
• مدل دادهای فیزیکی (Physical Data Model) مفاهیمی را فراهم میکند که توسط کاربران نهایی (End Users) بهراحتی قابل فهم باشند.
• مدل دادهای (Data Model) ابزاری برای حصول تجرید دادهها (Data Abstraction) است.
• DBMS مسئولیت کامل اینکه در هر لحظه پایگاه دادهها در وضعیت معتبر (Valid State) باشد را برعهده دارد. لازم به ذکر است وضعیت معتبر وضعیتی است که تمام محدودیتها و شرایط و ساختارهای تعریف شده در شمای پایگاه داده را ارضاء کند.
1 صفر
2 1
3 2
4 3
گزینه 3 صحیح است. بررسی عبارات:
عبارت اول:
این عبارت درست است.
در زبان سطح پایین دستکاری دادههای باید روند تغییرات دادهها برخلاف زبان سطح بالا قدم به قدم مشخص شوند. زبان سطح پایین باید حتما در یک زبان برنامهنویسی همه منظوره باشد اما زبان DML سطح بالا لازم نیست.
عبارت دوم:
این عبارت نادرست است.
مدل دادهای فیزیکی جزئیاتی را فراهم میکند که از نحوه ذخیره دادههای برروی محیط فیزیکی اطلاع میدهند. مفاهیم فراهم شده در این مدل سطح پایین به طور کلی برای متخصصان کامپیوتر میباشند و نه کاربران نهایی (End Users).
عبارت سوم:
این عبارت کاملا درست است.
به طور کلی Data abstraction به معنی مخفی کردن جزئیات ذخیرهسازی و سازماندهی دادهها و تنها نمایش جزئیات منطقی مثل موجودیتها و روابط میباشد.
Data Model که مجموعهای از مفاهیم برای بیان ساختار یک پایگاه دادهاست، ابزارهای لازم برای رسیدن به این abstraction را در اختیار قرار میدهد.
عبارت چهارم:
این عبارت نادرست است.
DBMS به طور کامل نه بلکه فقط تا حدی مسئول نگه داشتن پایگاهداده در حالت valid است.
آسان کدام نمودار بهترین توصیف برای عبارت زیر را نشان میدهد؟
طراحی پایگاه داده
«در اسناد تحلیل مربوط به امور تغذیه دانشجویان نوشته شده است: تمام غذاها این قابلیت را دارند که بهعنوان پیشغذای دیگر نیز استفاده شوند. بهعنوان مثال الویه که خود میتواند غذای مستقلی باشد، میتواند بهعنوان پیشغذای چلوخورشت قیمه به دانشجو داده شود. همچنین همراه با پیشغذا یک نوشیدنی یا ترشی (و نه هر دو با هم) به دانشجو داده میشود»
1 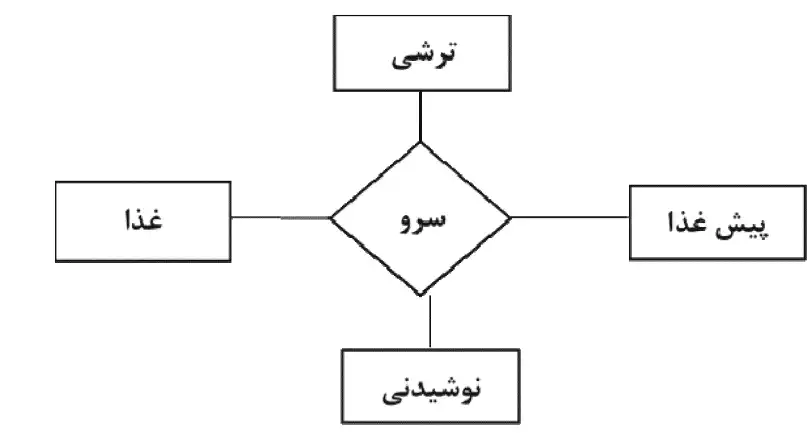
2 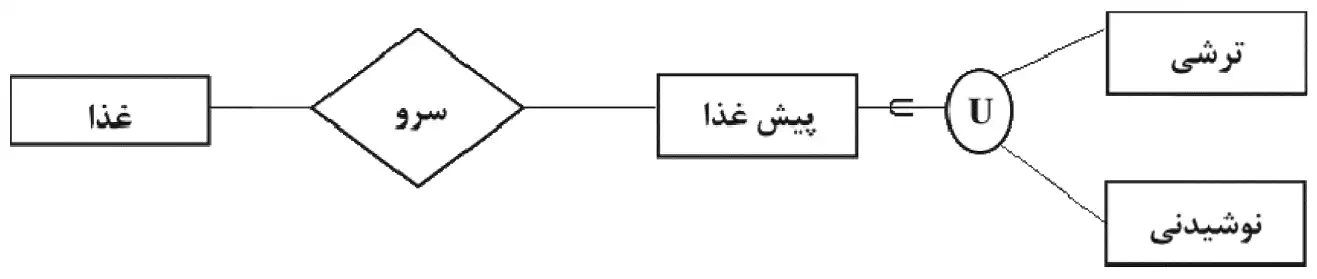
3 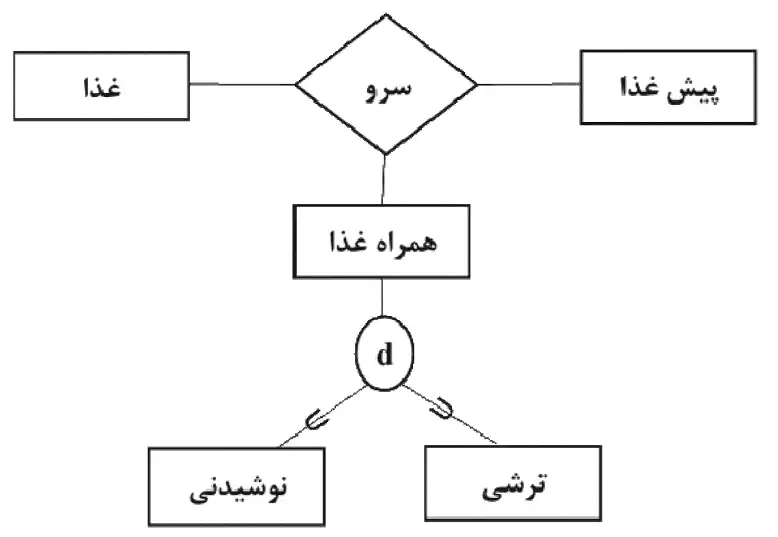
4 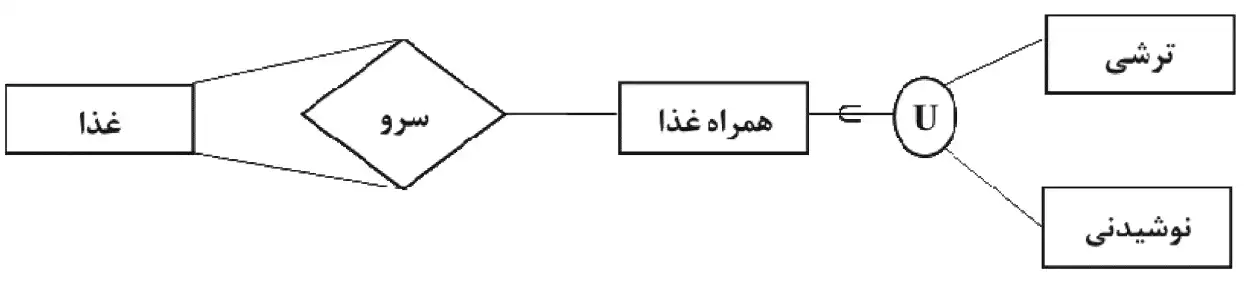
گزینه 4 صحیح است. بررسی اشکال:
شکل ۱:
در این شکل پیشغذا و غذا به عنوان دو موجودیت جداگانه معرفی شدهاند درحالیکه لازم به اینکار نیست زیرا همانطور که در پاراگراف آمده ذکر شده پیشغذا از میان همان غذاها انتخاب میشود بنابراین بودن یک موجودیت غذا کافیست.
همچنین در اینجا هم نوشیدنی و هم ترشی هر دو با هم در رابطه شرکت کردهاند امّا مطابق آنچه ذکر شده این دو همزمان با هم سرو نمیشوند، بنابراین بودنشان همزمان در رابطه درست نیست.
شکل ۲:
اجتماع نوشیدنی و ترشی باید موجودیت همراه غذا را تشکیل دهد نه پیشغذا.
پیشغذا همان غذاها هستند و نیازی به داشتن موجودیت جداگانه نمیباشند.
شکل ۳:
اینجا فقط مشکل وجود موجودیت پیشغذا است، زیرا پیشغذاها از همان موجودیت غذا میتوانند انتخاب شوند و نیاز به موجودیت جداگانه ندارند.
شکل ۴:
این شکل بهترین شکل برای توصیف پاراگراف آمده است.
به وضوح مشخص است که همراه غذا از اجتماع نوشیدنی و ترشی بدست میآید.
در هر سرو یک همراه غذا از نوشیدنی و یا ترشی سرو میشود که در این شکل به خوبی نمایش دادهشدهاست.
غذا و پیشغذا هر دو میتوانند از موجودیت غذا انتخاب شوند پس تعریف موجودیت دیگر لازم نیست و فقط کافیست که موجودیت غذا را دو بار در رابطه شرکت دهیم.
متوسط دو جدول زیر با وابستگیهای تابعی نشان داده شده مفروض است.
طراحی پایگاه داده
1) TblOne (A, B) , $\left\{A\to B\right\}$
2) TblTwo (A, C) , $\left\{A\to C\right\}$
حال اگر DE Normalization انجام دهیم، کدام مورد درست است؟
1 جدول حاصل نرمال سطح چهار است ولی در مورد نرمال بودن سطح پنجم نمیتوان اظهارنظر کرد.
2 جدول حاصل میتواند مشکل MVD (وابستگی چندمقداره) داشته باشد.
3 جدول حاصل نرمال سطح دوم نیست.
4 جدول حاصل نرمال سطح سوم نیست.
گزینه 2 با تاثیر مثبت در سنجش اعلام شد. گاهی اوقات دسترسی به برخی دادهها و انتخابها آنقدر پرکاربرد و زیاد میشوند که افزودن دادههای اضافی و برگرداندن پایگاه داده به یک سطح نرمال پایینتر برای ما از لحاط هزینه بهینهتر میباشد. فرآیند Denormalization برای همین منظور استفاده میشود.
توجه کنید این فرآیند دقیقا برعکس عمل normalization نیست و فقط براساس کاربردهای مورد نیاز انجام میشود.
برای مثال: فرض کنید که ما دو جدول از اساتید و دورهها داریم. در جدول دورههای ID اساتید ذخیره میشود امّا نام اساتید خیر. در اینجا ما اگر نیاز داشته باشیم که به دورهها به همراه نام اساتید دسترسی داشته باشیم باید هر بار این دو جدول را با یکدیگر پیوند بزنیم.
از یک لحاظ اینکار خوب است زیرا اگر استادی تصمیم به تغییر نامش بگیرد ما فقط کافی است آن نام را در یکجا تغییر دهیم.
ولی از طرف دیگر اگر این جدولها بزرگ باشند، ممکن است زمانهای زیادی هر بار صرف پیوند این جدول بکنیم. در اینجا denormalization برای حل این مشکل میآید و با ایجاد یک جدول از پیوند این دو جدول سرعت را افزایش میدهد.
در این سؤال با توجه به جداول داده شده، عمل Denormalization یک جدول از پیوند طبیعی دو جدول آمده به ما میدهد:
$NewTbl\ \left(A,\ B,C\right),\ \left\{A\to B,\ A\to C\right\}$
جدول بدست آمده در سطح 2NF است زیرا صفات B و C با کل کلید جدول که A است رابطه کامل دارند.
جدول بدست آمده در سطح 3NF است زیرا هیچ وابستگی انتقالی در رابطه وجود ندارد، به عبارتی هیچ یک از صفتها با کلید به دلیل وجود واسطه وابستگی تابعی ندارند بلکه مستقیم با خود کلید یعنی A رابطه دارند.
جدول بدست آمده میتواند مشکل MVD داشته باشد و در سطح 4NF نباشد. این مشکل اجباری نیست فقط امکانش هست. علت آن هم پیوند دو جدول با صفتی مشترک است.
تستهای درس مدارهای منطقی کنکور کامپیوتر ۱۴۰۲ به همراه جواب تشریحی
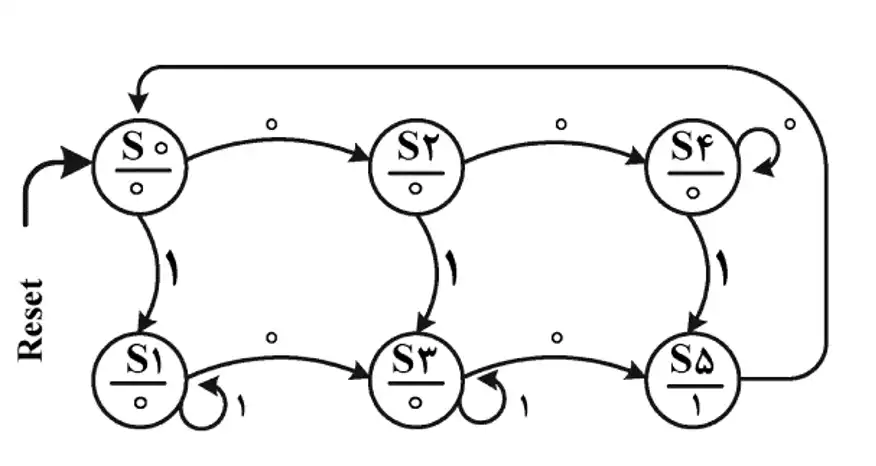
آسان ماشین حالت زیر چه رشتهای را
نمیتواند تشخیص دهد؟
تحلیل مدارات ترتیبی و پارامترهای زمانی فلیپ فلاپها
1 تعدادی صفر سپس یک
2 ابتدا صفر، تعدادی یک سپس صفر
3 تعدادی یک سپس صفر
4 تعدادی یک سپس صفر و تعدادی یک سپس صفر
به ترتیب گزینهها را بررسی میکنیم:
گزینه ۱:
با ۲ تا صفر به S4 میرویم سپس هر مقدار صفر که دریافت کنیم در همان حالت میمانیم تا اینکه با دریافت یک ۱ به S5 میرویم که حالت هدف است. بنابراین تعدادی صفر و سپس یک قابل تشخیص است.
گزینه ۲:
با یک صفر به S2 رفته سپس با یک ۱ به S3 میرویم، در اینجا هر چه قدر که ۱ بگیریم در همان حالت میمانیم، تا زمانیکه یک صفر دریافت کرده و به S5 میرویم که حالت هدف است. بنابراین ابتدا صفر، تعدادی یک سپس صفر قابل تشخیص است.
گزینه ۳:
با دریافت یک ۱ به S1 میرویم و تا زمانی که ۱ دریافت کنیم در همانجا میمانیم تا اینکه یک صفر دریافت کنیم که به S3 میرویم، در اینجا براساس گزینه دیگر ورودی دریافت نمیکنیم و چون در S3 که حالت هدف نیست قرار گرفتیم میتوانیم نتیجه بگیریم که این گزینه قابل تشخیص نیست.
گزینه ۴:
تعدادی یک ما را به S1 برده و در آنجا نگه میدارد، با دریافت یک صفر به S3 میرویم و با دریافت تعدادی یک همانجا میمانیم تا اینکه در نهایت با دریافت یک صفر به S5 رفته که حالت هدف است. بنابراین این گزینه قابل تشخیص است.
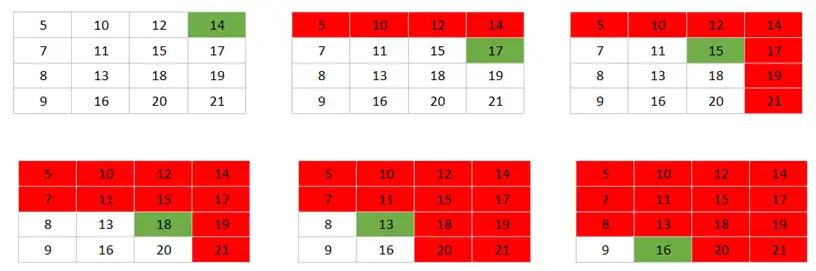
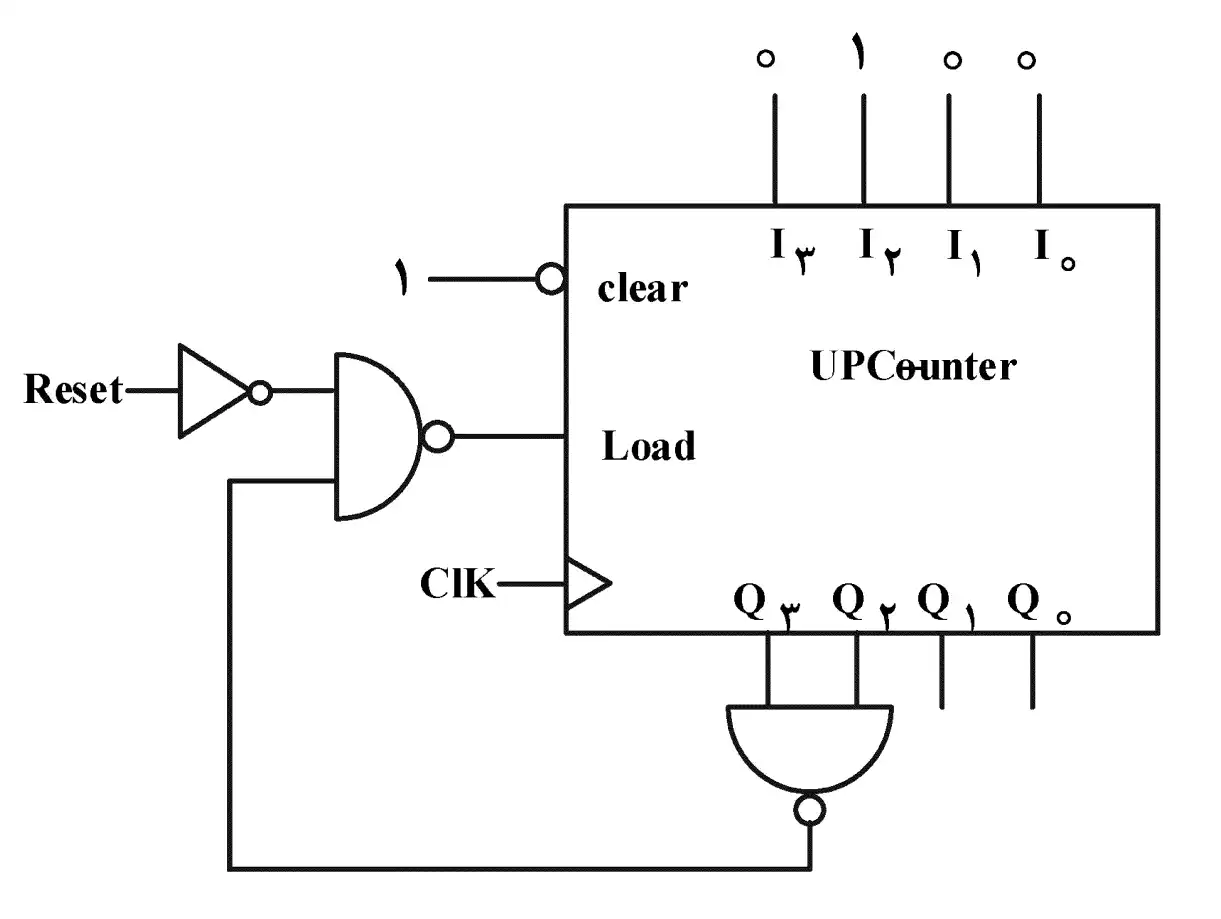
آسان شمارنده زیر چه ترتیبی را میشمارد؟
تحلیل مدارات ترتیبی و پارامترهای زمانی فلیپ فلاپها
1 از صفر تا دوازده
2 از چهار تا دوازده
3 از صفر تا پانزده
4 از چهار تا پانزده
به ورودیهای counter توجه کنید.
ورودی clear یک ۱ است که چون not میشود میتوان آن را صفر در نظر گرفت، بنابراین در این counter، clear عملی انجام نمیدهد.
حال به ورودی $I0$ تا $I3$ توجه کنید، این ورودی برابر عدد ۴ است.
در نهایت برای ورودی Load میتوانیم عبارت زیر را بنویسیم:
$\overline{(\overline{Reset}.\overline{\left(Q_3.Q_2\right)})}=Reset+(Q_3.Q_2)$
براساس ورودی Load اگر Q2 و Q3 هر دو همزمان ۱ باشند، خروجی در کلاک بعدی برابر ۴ یعنی مقدار $I$ ها میشود. به عبارتی اگر خروجی ۱۲ باشد در کلاک بعدی ۴ میشود و دیگر بالاتر نمیرود. بنابراین بیشترین مقدار شمارش ۱۲ است و کمترین مقدار چون ورودی clear عمل نمیکند و Reset نیز به Load وصل است (که آن هم نهایت ۴ را خروجی میدهد) ۴ است.
شمارنده از ۴ تا ۱۲ میشمارد.
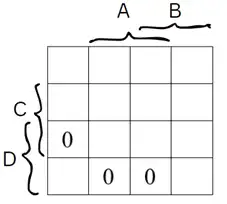
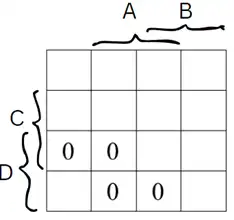
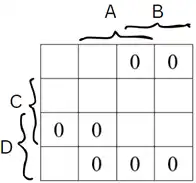
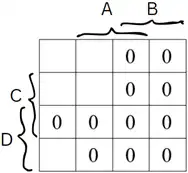
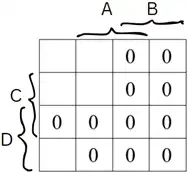
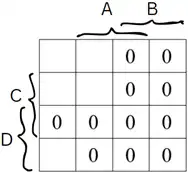
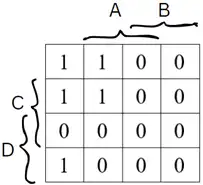
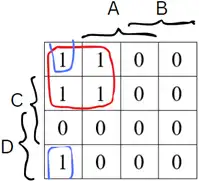
آسان عبارت سادهشدۀ تابع زیر کدام است؟
ساده سازی، جبر بول، گیتها
$F\left(A,B,C,D\right)=\left(A+B+\bar{C}+\bar{D}\right)\left(\bar{A}+C+\bar{D}\right)\left(\bar{A}+B+\bar{C}+\bar{D}\right)\left(\bar{B}+C\right)\left(\bar{B}+\bar{C}\right)\left(A+\bar{B}\right)\left(\bar{B}+D\right)$
1 $\bar{B}\left(\bar{D}+\bar{A}\bar{C}\right)$
2 $\bar{A}\bar{B}+\bar{B}\bar{D}$
3 $\bar{B}\left(\bar{A}+\bar{D}\right)$
4 $\bar{B}\left(\bar{C}+\bar{D}\right)$
عبارت F داده شده به صورت product-of-sums است بنابراین سریعترین راه برای ساده کردن آن استفاده از جدول کارنو است.
فقط توجه کنید که در اینجا چون product-of-sums داریم باید برای هر پرانتز مکانهایی که در آن صفر میشود (به عبارتی ماکسترمها) را پیدا کنید و علامت بزنید. این کار را با معکوس کردن هر پرانتز میتوانید به راحتی انجام دهید. چگونه؟
برای مثال در ابتدا برای پرانتز اول معکوس آن میشود $(~\overline{A}.\overline{B}.C.D)$ حال باید مکانهایی که هر ۴ عبارت برقرار هستند را پیدا کرده و در آن صفر بگذارید.
به سراغ پرانتز بعدی میرویم و همین کار را تکرار میکنیم: $(\bar A +C+\bar D )→(A.\bar C .D)$
$(\bar A +B+\bar C +\bar D )→(A.\bar B .C.D)$
$(\bar B +C)→(B.\bar C )$
$(\bar B +\bar C)→(B.C)$
$(A+\bar B)→(\bar A.B)$
$(\bar B+\bar D )→(B.D)$
در نهایت جدول کارنو به صورت زیر در میآید که چون تعداد یکهای آن کمتر از صفرهاست سعی میکنیم کوچکترین عبارت sum-of-products آن را بدست آوریم:
عبارت نهایی برابر است با:
$F\left(A,B,C,D\right)=\overline{B}\overline{D}+\overline{A}\overline{B}\overline{C}=\overline{B}\left(\overline{D}+\overline{A}\overline{C}\right)$
بنابراین گزینه ۱ صحیح است.
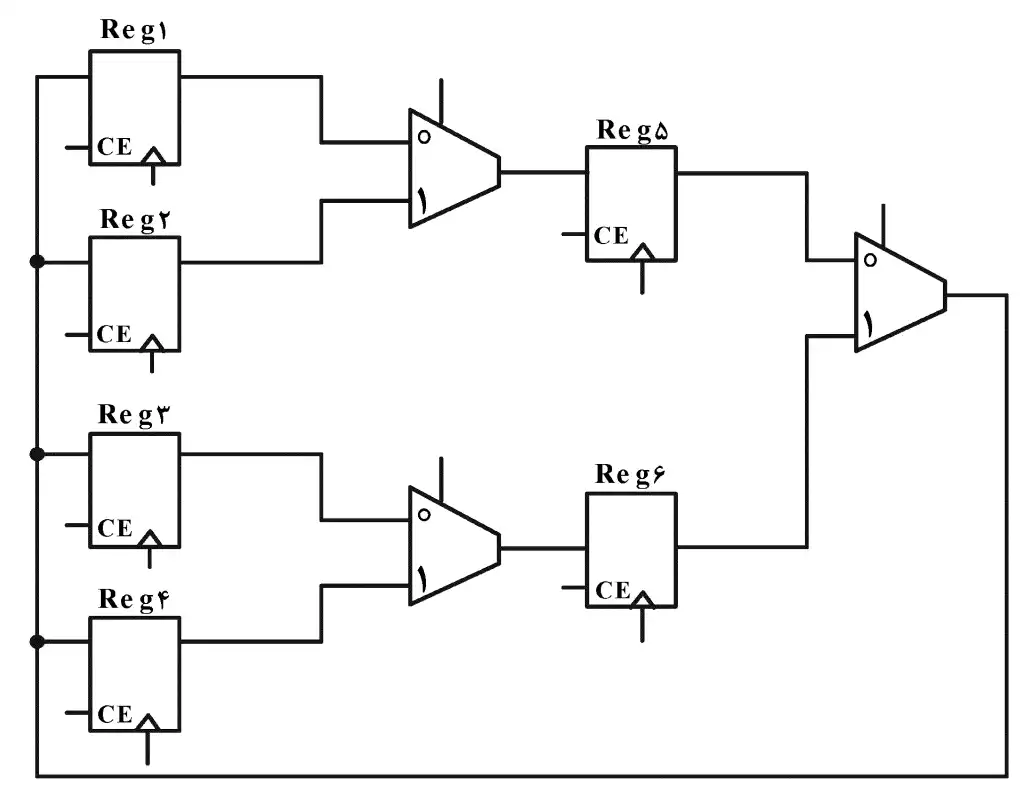
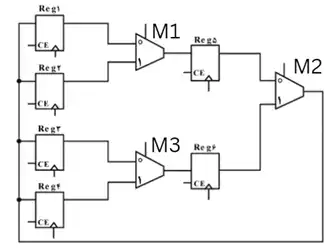
آسان در مدار زیر، حداقل تعداد سیکلهای لازم جهت جابهجایی (Swap) محتوای ثباتهای Reg1 و Reg4 کدام است؟ (فرض کنید که Select مالتی پلکسرها و Clock Enable (CE) ثباتها توسط ماشین حالت مناسب تولید خواهد شد.)
تحلیل مدارات ترتیبی و پارامترهای زمانی فلیپ فلاپها
1 2
2 3
3 4
4 مسیرهای لازم برای این جابهجایی وجود ندارد.
نامهای مشخص شده در شکل زیر را برای مالتیپلکسرها در نظر میگیریم و برای مشخص کردن کلید Enable هر رجیستر از حرف E و عدد هر رجیستر استفاده میکنیم.
در کلاک اول: مقادیر زیر را وارد مدار میکنیم (توجه مقادیر ورودیهایی که مشخص نشدهاند همگی صفر است.):
$M_1=0,\ M_3=1,\ M_2=0,\ E_5=1,\ E_6=1$
در این کلاک مقدار رجیستر ۱ به رجیستر ۵ و مقدار رجیستر ۴ به رجیستر ۶ منتقل میشوند.
در کلاک دوم: (توجه مقادیر ورودیهایی که مشخص نشدهاند همگی صفر است.)
$M_2=0,E_4=1$
در این کلاک مقدار رجیستر ۱ که در رجیستر ۵ هم قرار دارد به رجیستر ۴ منتقل میشود.
در کلاک سوم: (توجه مقادیر ورودیهایی که مشخص نشدهاند همگی صفر است.)
$M_2=1,E_1=1$
در این کلاک مقدار رجیستر ۴ که در رجیستر ۶ هم قرار دارد به رجیستر ۱ منتقل میشود.
در این لحظه دو مقدار مطابق خواسته سؤال جابهجا شدهاند بنابراین حداقل ۳ کلاک برای اینکار لازم است.
(توجه: اعمال دو کلاک دو و سه میتوانند جابهجا نیز رخ دهند.)
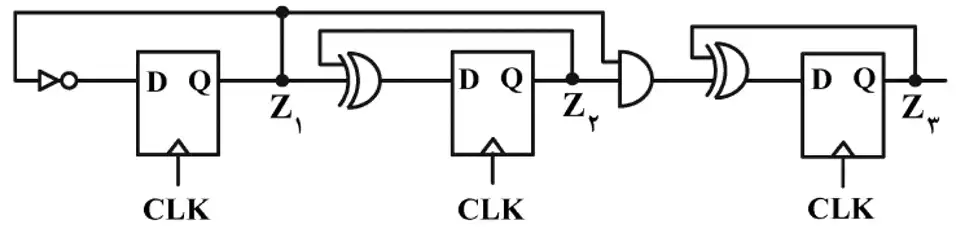
متوسط با این فرض که سیگنال CLK فرکانس 160 MHz داشته باشد، فرکانس سیگنال $Z_3$ چند مگاهرتز است؟
تحلیل مدارات ترتیبی و پارامترهای زمانی فلیپ فلاپها
1 10
2 80
3 40
4 20
ابتدا ورودی D تمام فلیپفلاپها را بدست میآوریم: (به یاد داشته باشید که در فلیپفلاپ D خروجی Q در کلاک بعدی برابر مقدار D فعلی است.)
$D_1=\overline{Z_1},\ \ D_2=Z_1\bigoplus Z_2,\ \ D_3=Z_1.Z_2\bigoplus Z_3$
با شروع از $Z_3 Z_2 Z_1=000$ سعی میکنیم یک دوره کامل از تغییرات از این ۳ سیگنال را بیابیم. این کار را با توجه به ۳ عبارت بالا انجام میدهیم:
$000→001→010→011→100→101→110→111→000$
همانطور که میبینید پس از ۸ کلاک (تعداد پیکانها) یک دوره کامل تغییرات ۳ سیگنال طی شده و دوباره به مقدار 000 میرسیم. چون فرکانس کلال 160MHz است فرکانس هر دوره برابر $\frac{160}{8}=20MHz$ میشود.
حال توجه کنید که در هر دوره مقدار $Z_3$ یکبار از صفر به ۱ و یکبار از ۱ به صفر میرود بنابراین در هر دوره تنها یک حلقه طی میکند و فرکانسش با دوره یکی است. یعنی فرکانس $Z_3$ نیز برابر 20MHz است.
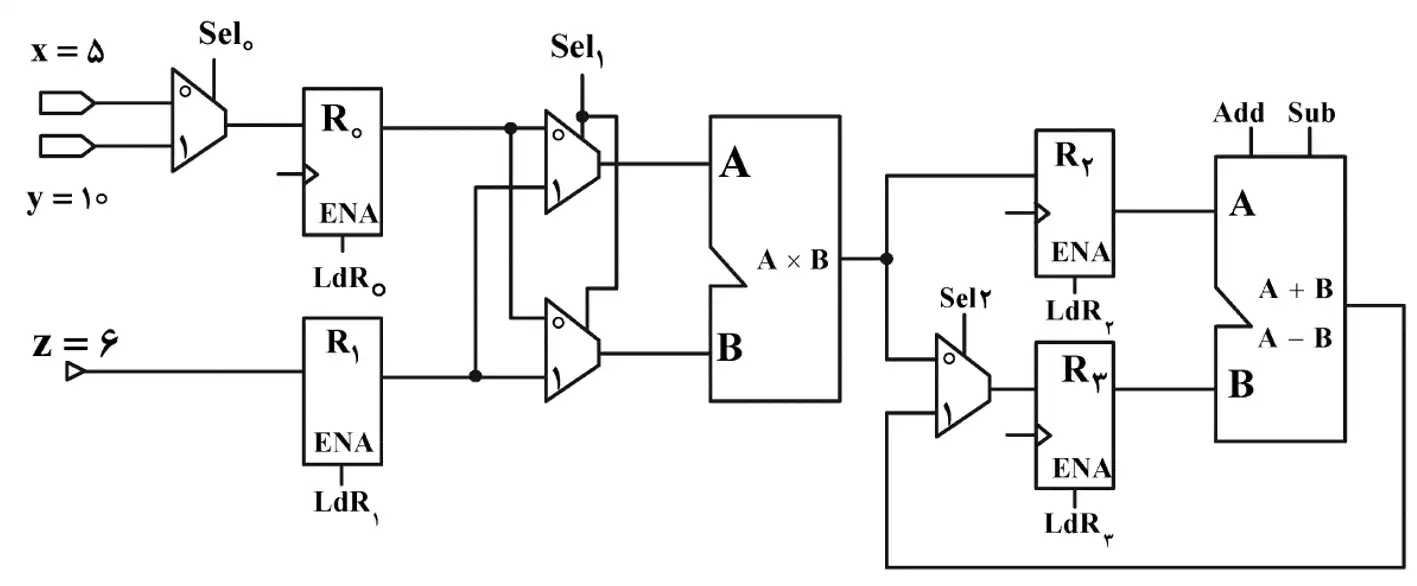
متوسط مدار زیر به همراه سیگنالهای کنترلی مشخص شده طی 5 سیکل داده شده است. مقدار ثبات $R_3$ پس از 5 سیکل کدام است؟
تحلیل مدارات ترتیبی و پارامترهای زمانی فلیپ فلاپها
سیکل 1: $Sel_0=0$، $LdR_0=1$، $LdR_1=1$
سیکل 2: $Sel_1=0$، $LdR_2=1$
سیکل 3: $Sel_0=1$، $LdR_0=1$، $Sel_1=1$، $Sel_2=0$، $LdR_3=1$
سیکل 4: $Sub = 1$، $LdR_3=1$، $Sel_2=1$، $Sel_1=0$، $LdR_2=1$
سیکل 5: $Add = 1$، $LdR_3=1$، $Sel_2=1$
1 25
2 89
3 111
4 161
با توجه به دستورات در هر سیکل داریم.
در سیکل اول:
عدد ۵ به رجیستر صفر و عدد ۶ به رجیستر یک منتقل میشوند.
در سیکل دوم:
(توجه کنید $Sel_1$ به دو مالتی پلکسر که به ضربکننده متصل هستند، وصل است)
مقدار ذخیره شده در رجیستر صفر در خودش ضرب شده و حاصل به رجیستری دو میرود. در نتیجه مقدار رجیستر دو برابر $5×5=25$ میشود.
در سیکل سوم:
در این سیکل دو اتفاق میافتد:
۱- مقدار ۱۰ به رجیستر صفر منتقل میشود.
۲- مقدار رجیستر یک در خودش ضرب شده و حاصل در رجیستر سه ذخیره میشوند. مقدار رجیستر یک برابر ۶ است بنابراین مقدار $6×6=36$ در رجیستر سه ذخیره میشود.
در سیکل چهارم:
در این سیکل دو اتفاق میافتد:
۱- مقادیر دو رجیستر دو و سه از هم کم شده و حاصل در رجیستر سه ذخیره میشود. مقدار رجیستر دو ۲۵ و رجیستر سه ۳۶ است بنابراین مقدار نهایی رجیتسر سه به $25-36=-11$ میرسد.
۲- مقدار فعلی رجیستر صفر که ۱۰ است در خودش ضرب شده و حاصل در رجیستر دو ذخیره میشود. بنابراین در انتهای این سیکل مقدار رجیستر دو برابر $10×10=100$ است.
در سیکل پنجم:
در این سیکل مقدار فعلی رجیستر دو که ۱۰۰ است با مقدار رجیستر سه که ۱۱- است جمع شده و حاصل به رجیستر سه منتقل میشود. بنابراین مقدار رجیستر سه به $100-11=89$ میرسد.
مقدار نهایی رجیستر سه برابر ۸۹ است.
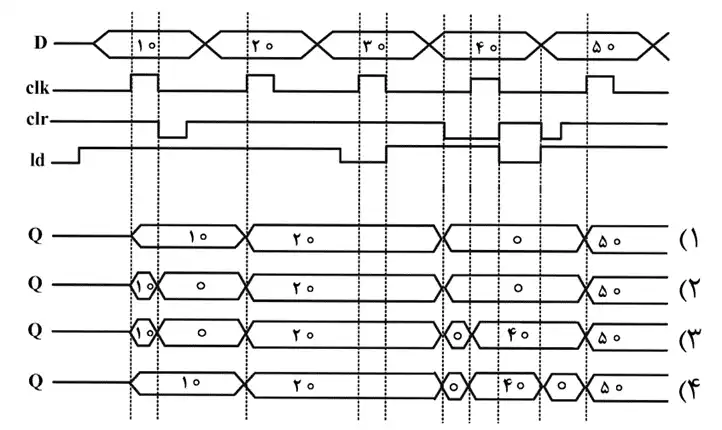
متوسط کد Verilog/VHDL زیر را در نظر بگیرید. با توجه به مقادیر ورودیها که بهصورت شکل موج داده شده است، خروجی Q کدام است؟
تحلیل مدارات ترتیبی و پارامترهای زمانی فلیپ فلاپها
Verilog
Module ParReg(D, Id, clr, clk, Q);
input D, Id, clr, clk; output Q;
wire [7 : 0] D; wire Id, clr, clk;
reg [7 : 0] Q;
always@(posedge clk or negedge clr)
if (!clr) begin
Q = 0;
end else begin
if (Id) begin
Q = D;
end
end
end module;
VHDL
entity ParReg is
port (D: in bit_vector; clk, Id: in bit; Q: out bit_vector);
end entity ParReg;
architecture RTL of ParReg is
begin
L : Process (clk, clr)
begin
if (clr = ‘0’) then
Q <= (others => ‘0’)
elseif (clk ‘ event and clk = ‘1’) then
if (Id = ‘1’) then
Q <= D;
end if;
end if;
end process;
end architecture RTL;
1 1
2 2
3 3
4 4
طبق کدها متوجه میشویم که clear پایهی active low و آسنکرون با کلاک است، در لبه مثبت اول کلاک، کلیر 1 (غیر فعال) و لود نیز 1 (فعال) است. طبق کدها در این شرایط میتوان ورودی D را به خروجی Q انتقال داد (که این مورد در همه گزینهها رعایت شده). حال وقتی در خطچین دوم، لبه کلاک منفی میشود (پایین میرود) و کلیر صفر میشود، مقدار خروجی بدون توجه به سایر پایهها صفر خواهد شد (چون کلیر آسنکرون تنظیم شده است) به این ترتیب گزینههای 1 و 4 رد میشوند چون مقدار خروجی را همچنان 10 نگه داشتهاند. بین گزینههای 2 و 3 تفاوت وقتی دیده میشود که از لبه سوم کلاک عبور کردهایم و clear = 0 میشود. در این لحظه با توجه به مقدار کلیر، باید Q = 0 شود که در هر 2 گزینه رعایت شده اما در گزینه سوم وقتی لبه بالارونده چهارم کلاک آمده و البته LD هم یک شده، مقدار D را به Q انتقال داده است که اشتباه است چون در این لحظه همچنان clear = 0 است و نمیتوان خروجی را 1 کرد.
تستهای درس معماری کامپیوتری کنکور کامپیوتر ۱۴۰۲ به همراه جواب تشریحی
آسان اگر یک کامپیوتر از نمایش اعداد مکمل 2 و ثباتهای 12 بیتی استفاده کند، دامنه نمایش اعداد صحیح در آن کدام است؟ محاسبات
1 از –2048 تا +2047
2 از –2047 تا +2047
3 از –4096 تا +4095
4 از –4095 تا +4095
از میان ۱۲ بیت، ۱ بیت به عنوان بیت علامت استفاده میشود و دیگر بیتها برای مقادیر اعداد. با ۱۱ بیت میتوان از 0 تا $2^{11}-1=2047$ را نمایش داد. توجه داشته باشید که در سیستم مکمل ۲ اعداد منفی قابل نمایش یکی بیشتر از مثبتها است.
براساس این توضیحات دامنه نمایش اعداد برای اعداد مثبت حداکثر 247 و برای اعداد منفی حداقل عدد -248 است.
بنابراین گزینه ۱ صحیح است.
آسان در یک سامانه پردازشی، %40 زمان برای دسترسی به حافظه RAM و %30 زمان برای دسترسی به هارد دیسک صرف میشود. اگر سرعت دسترسی به حافظه RAM و دیسک را بهترتیب دو و سه برابر کنیم، تسریع چقدر میشود؟ ارزیابی کارایی
1 1.33
2 1.5
3 1.66
4 2.5
اگر T زمان کل مصرفی در سامانه پردازشی باشد داریم:
$T=T_R+T_H+T_O$
$T_R$ : زمان مصرف شده توسط RAM
$T_H$ : زمان مصرف شده توسط هارددیسک
$T_O$ : زمان مصرف شده توسط باقی اجزاء پردازش
براساس توضیحات سؤال داریم:
$T_R=0.4T,T_H=0.3T,T_O=0.3T$
پس از افزایش سرعت زمان مصرفی RAM نصف شده و زمان هارددیسک $\frac{1}{3}$ میشود. اگر $T'$ را به عنوان زمان مصرفی جدید بگیریم داریم:
$T'=\frac{T_R}{2}+\frac{T_H}{3}+T_O=0.2T+0.1T+0.3T=0.6T$
چون سرعت و زمان مصرف شده رابطه عکس با هم دارند، میتوانیم نسبت سرعتها را با محاسبه عکس نسبت زمانهای مصرفی بدست آوریم:
$\frac{S'}{S}=\frac{T}{T'}=\frac{T}{0.6T}\approx 1.66$
متوسط میخواهیم برای یک بانک ثبات (Register File) شامل 4 ثبات 4 بیتی مداری طراحی کنیم که امکان انتخاب دو ثبات بهعنوان ورودی به واحد ALU و یک ثبات بهعنوان محل نگهداری خروجی ALU نیاز داشته باشد. برای طراحی این مدار (بهغیر از ثباتها) به کمک دیکودر و مالتی پلکسر به چه مشخصاتی نیاز است؟ طراحی کامپیوتر
1 سه رمزگشای $(decoder) 2\times4$ و 16 بافر سه حالته
2 دو رمزگشای $(decoder) 2\times4$ و 16 بافر سه حالته
3 دو رمزگشای $(decoder) 2\times4$ و 32 بافر سه حالته
4 سه رمزگشای $(decoder) 2\times4$ و 32 بافر سه حالته
چون باید ۳ ثبات برای ۲ ورودی و ۱ خروجی ALU انتخاب کنیم نیاز به سه decoder داریم که چون ۴ ثبات داریم decoderها باید 2x4 باشند.
خروجی ALU را به ورودی ۴ ثبات وصل میکنیم و ثباتی را که میخواهیم خروجی در آن ذخیره شود را بایک decoder مشخص میکنیم.
برای ورودیهای ALU باید دو ثابت انتخاب کنیم برای اینکار به ۱۶ بافر سه حالته برای هر ورودی نیاز داریم. ۱۶ بافر برای این است که ثباتها ۴ بیتی بوده و ما ۴ تا ثبات داریم و باید هر بیت خروجی ثبات را با یک بافر سه حالته کنترل کنیم (به یاد داشته باشید که بافر سه حالته یک ورودی کنترل دارد که اگر ۱ باشد خروجی برابر ورودی دیگر المان است و اگر صفر باشد خروجی high impedance است.)
بنابراین در کل به ۳ دیکدر و ۳۲ بافر سه حالته نیاز داریم.
آسان یک کامپیوتر دارای دستورات و حافظهای با کلمات 32 بیتی، 8 ثبات و 112 دستورالعمل است. هر دستورالعمل از یک بخش Opcode و دو میدان (Field) آدرس تشکیل شده است: یکی برای ثبات و یکی برای حافظه. میتوان از حافظه در هر ثبات و یا بالعکس، از ثبات در خانهای از حافظه نوشت. امکان جابهجایی مستقیم داده بین خانههای حافظه وجود ندارد. تعداد بیتهای مورد نیاز برای میادین مختلف دستورات کدام است؟ (Opcode, RegAddr, MemAddr) طراحی کامپیوتر
1 (21, 3, 8) بیت
2 (22, 3, 7) بیت
3 (3, 22, 7) بیت
4 (16, 8, 8) بیت
برای RegAddr چون ۸ تا رجیستر داریم $log_2 \ 8=3$ بیت برای دسترسی به آنها کافی است.
برای Opcode نیز چون ۱۱۲ تا دستورالعمل داریم تعداد $⌈log_2\ 112 ⌉=7$ بیت برای مشخص کردن آنها کافی است.
توجه کنید حافظه کلمات ۳۲ بیتی دارد بنابراین هر دستور میتواند ۳۲ بیت باشد. ۱۰ بیت را برای دو قسمت قبل استفاده کردیم بنابراین میتوان $32-10=22$ بیت باقی مانده را برای دسترسی به خانههای حافظه در نظر گرفت.
بنابراین جواب نهایی برابر (7,3,22) است.
آسان یک حافظه نهان (Cache) دارای نگاشت مستقیم (Direct Mapping) و ظرفیت 1 MB و حافظه اصلی دارای ظرفیت 512 MB است. بلوکهای حافظه هرکدام 32 بایتی هستند. میادین مختلف آدرس (Tag, Block, Word Offset) چند بیتی هستند؟ حافظه ها
1 (5, 15, 9) بیت
2 (5, 15, 12) بیت
3 (5, 18, 9) بیت
4 (5, 14, 10) بیت
در روش Direct Mapping سه بخش آدرس به صورت زیر بدست میآیند:
Word offset به راحتی از روی گزینههای مشخص است که ۵ است، آن هم به دلیل ۳۲ بایتی بودن بلوکهای حافظه است که از طریق $log_232=5$ بدست آمده است.
تعداد بیتهای مورد نیاز Block با محاسبه $log_2$ تعداد Blockهایی که حافظه Cache میتواند ذخیره کند تعیین میشود. در این جا Cache ظرفیت $1MB=2^{20} B$ دارد و هر بلاک $32B=2^5 B$ حافظه نیاز دارد بنابراین:
$\frac{2^{20}}{2^5}=2^{15}\ Block\to {{\mathrm{log}}_2 2^{15}\ }=15\ bits\ for\ Block$
تعداد بیتهای tag برابر اختلاف تعداد بیتهای لازم برای آدرسدهی حافظه اصلی و Cache میباشد. تعداد بیتهای لازم برای Cache برابر ۲۰ است که حاصل جمع Block و Word offset میباشد. تعداد بیتهای لازم برای حافظه اصلی برابر $log_2512M=log_22^{29}=29$ است. در نتیجه تعداد بیتهای tag برابر است با:
$29-20=9\ bits\ for\ Tag$
آسان با فرض اینکه X آدرس یک خانه در حافظه است، این برنامه RTL معادل اجرای کدام دستور است؟
RTL
t0: MAR <= X
t1: DR <= M[MAR]
t2: M[MAR] <= A
t3: A <= DR
1 STA X
2 LDA X
3 COMP A,X
4 XCHG A,X
به ترتیب خطوط دستورات را بررسی میکنیم:
در دستور اول، مقدار موجود در حافظه X به یک رجیستر به اسم MAR منتقل میشود.
در دستور دوم، از مقدار ذخیره شده در MAR به عنوان آدرس برای دسترسی به حافظه استفاده میشود و داده موجود در آن آدرس را در رجیستری به اسم DR میریزد.
در دستور سوم، مقدار A در حافظهای با آدرسی که در MAR ذخیره شده است منتقل میشود. این خانهی حافظه همان خانه حافظه در مرحله قبل است و MAR مقدارش برابر با X است. A یک رجیستر است.
در دستور چهارم، مقدار DR در A ریخته میشود. DR با توجه به دستورات قبل مقدارش برابر با M[MAR] است.
با توجه به این توضیحات، میتوان گفت که این دستورات مقدار ذخیره شده در M[MAR] یا همان M[X] را با مقدار ذخیره شده در رجیستر A جابهجا میکنند. بنابراین گزینه جواب باید XCHG A, X باشد.
بررسی گزینههای دیگر:
گزینه ۱:
این گزینه مقدار A را در حافظه با آدرس X منتقل میکند.
گزینه ۲:
این دستور مقدار خانه حافظه به آدرس X را به A منتقل میکند.
گزینه ۳:
Comp->Compare
این گزینه گویا به مقایسه مقدار حافظه در آدرس X و مقدار A میپردازد.
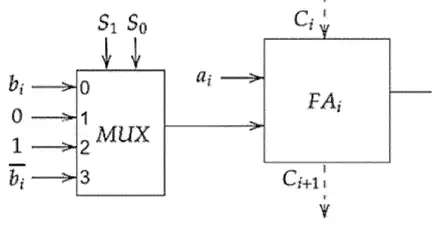
آسان شکل زیر جزء i اُم یک واحد حسابی (Arithmetic Unit) n بیتی است که عملکرد آن با خطوط $S_1S_0$ برای ورودیهای n بیتی A و B و تک بیت Cin، کنترل میشود. $FA_i$ یک تمام افزا (Full Adder) است.
طراحی کامپیوتر
اگر $S_1=1$، کدام حالت مربوط به عملکرد این واحد حسابی است؟
1
| $F$ |
$C_{in}$ |
$S_0$ |
$S_1$ |
| A-1 |
0 |
0 |
1 |
| A |
1 |
0 |
1 |
| A-B-1 |
0 |
1 |
1 |
| A-B+1 |
1 |
1 |
1 |
2
| $F$ |
$C_{in}$ |
$S_0$ |
$S_1$ |
| A-1 |
0 |
0 |
1 |
| A |
1 |
0 |
1 |
| A-B-1 |
0 |
1 |
1 |
| A-B |
1 |
1 |
1 |
3
| $F$ |
$C_{in}$ |
$S_0$ |
$S_1$ |
| A |
0 |
0 |
1 |
| A-1 |
1 |
0 |
1 |
| A-B-1 |
0 |
1 |
1 |
| A-B |
1 |
1 |
1 |
4
| $F$ |
$C_{in}$ |
$S_0$ |
$S_1$ |
| A |
0 |
0 |
1 |
| A+1 |
1 |
0 |
1 |
| A-B |
0 |
1 |
1 |
| A-B+1 |
1 |
1 |
1 |
وقتی $S_1=1$ است یعنی MUX بسته به مقدار $S_0$ تنها میتواند ۱ و $\overline{b_i}$ را خروجی دهد.
در اینجا به یک نکته توجه کنید شکل نمایش داده شده بیانگر یک بیت از دو ورودی و خروجی است، و وقتی با i آن را نمایش دادهاند به معنی این است که برای تمام بیتها عمل یکسانی صورت میگیرد. بنابراین وقتی ۱ به عنوان خروجی MUX انتخاب میشود به این معنی است که یک عدد با بیتهای تمام ۱ با عدد A جمع میشود و ما میدانیم که جمع شدن با یک عدد تمام یک، معادل با جمع شدن با عدد ۱- است.
با این توضیحات داریم:
اگر $S_0=0$, $C_{in}=0$ باشد، خروجی MUX برابر ۱ است و ما چون carry نداریم Full adders جمع یک عدد تمام یک با A را محاسبه میکند که معادل A-1 است.
اگر $S_0=0$, $C_{in}=0$ باشد، مانند قبل اتفاق میافتد با این تفاوت که یک ۱ نیز بدلیل وجود carry به حاصل اضافه میشود که حاصل را برابر A میکند.
اگر $S_0=1$, $C_{in}=0$ باشد، عدد A با مکمل ۱ عدد B جمع میشود که جمع با مکمل یک معادل با $A-B-1$ است.
اگر $S_0=1$, $C_{in}=1$ باشد، مانند قبلی اتفاق میافتد با این تفاوت که یک ۱ نیز اضافه میشود $A-B$.
روش دوم: استفاده از دوره های نکته و تست درس های کنکور کامپیوتر
شما با تهیه دوره نکته و تست هر درس از دروس رشته مهندسی کامپیوترمعرفی و بررسی دروس رشته مهندسی کامپیوتر در این صفحه تمامی دروس رشته کامپیوتر بطور کامل معرفی شده است، همچنین سرفصل هر یک از این دروس و منابع آن نیز برای شما عزیزان معرفی شده است میتوانید به پاسخ تشریحی تمامی تستهای کنکور، از اولین سال برگزاری دسترسی داشته باشید. علاوه بر روش سنتی حل تستها، روشهایی بیان میشود که با استفاده از آنها میتوان بسیاری از تستها را در زمان کمتری حل کرد.
در این صفحه تمامی دروس رشته کامپیوتر بطور کامل معرفی شده است، همچنین سرفصل هر یک از این دروس و منابع آن نیز برای شما عزیزان معرفی شده است میتوانید به پاسخ تشریحی تمامی تستهای کنکور، از اولین سال برگزاری دسترسی داشته باشید. علاوه بر روش سنتی حل تستها، روشهایی بیان میشود که با استفاده از آنها میتوان بسیاری از تستها را در زمان کمتری حل کرد.
پاسخنامه کنکور ارشد کامپیوتر
روش دیگری که میتوانید به پاسخ کلیدی (و نه تشریحی) تست های کنکور ارشد کامپیوتر ۱۴۰۲ دسترسی داشته باشید، استفاده از دفترچه کنکور کامپیوتر سال ۱۴۰۲ است. میتوانید از صفحه دفترچه سوالات کنکور ارشد مهندسی کامپیوتردانلود سوالات کنکور ارشد کامپیوتر دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند تمامی دفترچههای کنکور کامپیوتر را بهصورت رایگان دانلود کنید.
دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند تمامی دفترچههای کنکور کامپیوتر را بهصورت رایگان دانلود کنید.
کلید کنکور ارشد کامپیوتر ۱۴۰۲
در تصویر زیر میتوانید کلید کنکور ارشد کامپیوتر ۱۴۰۲ را ملاحظه فرمایید. در واقع کلید کنکور ارشد همان پاسخنامهای است که توسط سازمان سنجش برای کنکور ارائه میشود.
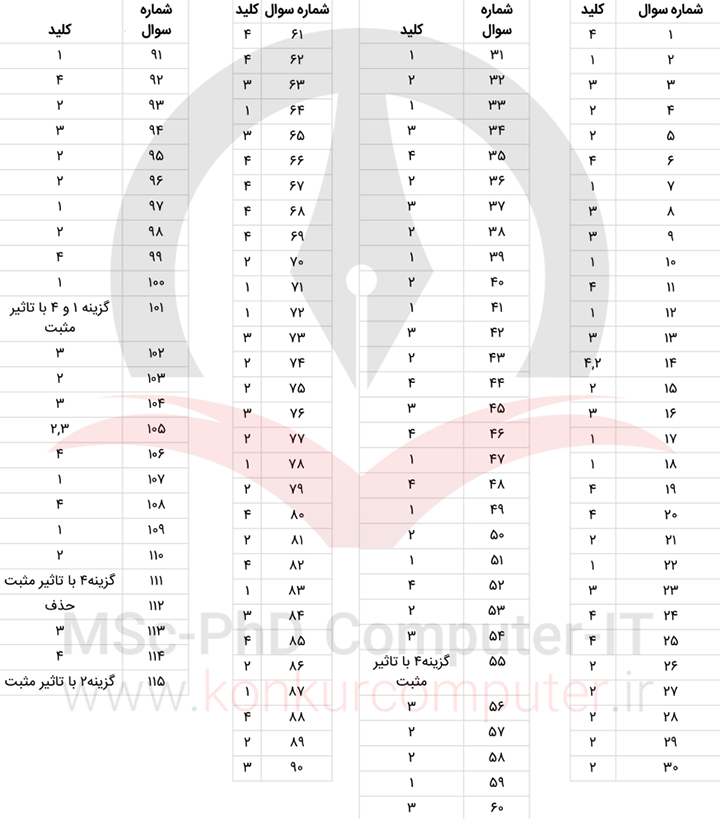
جمعبندی
آزمون کارشناسی ارشد کامپیوترمعرفی ارشد کامپیوتر ارشد کامپیوتر چیست؟
این مقاله عالی به معرفی ارشد کامپیوتر میپردازد و درباره آینده رشته کامپیوتر و نحوه اپلای کردن توضیح میدهد شامل سوالات متنوعی از جمله طراحی الگوریتمآموزش طراحی الگوریتم به زبان ساده
ارشد کامپیوتر چیست؟
این مقاله عالی به معرفی ارشد کامپیوتر میپردازد و درباره آینده رشته کامپیوتر و نحوه اپلای کردن توضیح میدهد شامل سوالات متنوعی از جمله طراحی الگوریتمآموزش طراحی الگوریتم به زبان ساده درس طراحی الگوریتم یکی از مهمترین و بنیادیترین دروس رشته کامپیوتر است. هدف از این درس، معرفی روشهای مختلف طراحی الگوریتمها برای حل مسائل گوناگون است، در این صفحه به معرفی و آموزش طراحی الگوریتم پرداخته شده است. و ساختمان دادهآموزش ساختمان داده و الگوریتم
درس طراحی الگوریتم یکی از مهمترین و بنیادیترین دروس رشته کامپیوتر است. هدف از این درس، معرفی روشهای مختلف طراحی الگوریتمها برای حل مسائل گوناگون است، در این صفحه به معرفی و آموزش طراحی الگوریتم پرداخته شده است. و ساختمان دادهآموزش ساختمان داده و الگوریتم هر ساختمان داده یک نوع فرمت ذخیرهسازی و مدیریت دادهها در کامپیوتر است، که امکان دسترسی و اصلاح کارآمد آن دادهها را برای یکسری از الگوریتمها و کاربردها فراهم میکند، در این صفحه به بررسی و آموزش ساختمان داده و الگوریتم پرداخته شده است، شبکهجامعترین آموزش درس شبکه های کامپیوتری
هر ساختمان داده یک نوع فرمت ذخیرهسازی و مدیریت دادهها در کامپیوتر است، که امکان دسترسی و اصلاح کارآمد آن دادهها را برای یکسری از الگوریتمها و کاربردها فراهم میکند، در این صفحه به بررسی و آموزش ساختمان داده و الگوریتم پرداخته شده است، شبکهجامعترین آموزش درس شبکه های کامپیوتری درس شبکه های کامپیوتری یکی از مهمترین و بنیادیترین دروس رشته کامپیوتر است، با توجه به اینکه اینترنت امروزی بزرگترین سیستم مهندسی ساخت دست بشر در تمام طول تاریخ است، آشنایی با شبکههای کامپیوتری برای تمامی علاقهمندان و دانشجویان رشته کامپیوتر الزامی است، در این راستا در این صفحه به معرفی شبکههای کامپیوتری پرداخته شده است، هوش مصنوعیدرس هوش مصنوعی
درس شبکه های کامپیوتری یکی از مهمترین و بنیادیترین دروس رشته کامپیوتر است، با توجه به اینکه اینترنت امروزی بزرگترین سیستم مهندسی ساخت دست بشر در تمام طول تاریخ است، آشنایی با شبکههای کامپیوتری برای تمامی علاقهمندان و دانشجویان رشته کامپیوتر الزامی است، در این راستا در این صفحه به معرفی شبکههای کامپیوتری پرداخته شده است، هوش مصنوعیدرس هوش مصنوعی این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده و ... است. داوطلبان برای پاسخگویی به این سوالات نیاز به دانش عمیق و تسلط بر مباحث مورد نظر دارند و لازم است که از منابع مناسبی مانند دوره نکته و تست و پلتفرم آزمون استفاده کنند.
این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده و ... است. داوطلبان برای پاسخگویی به این سوالات نیاز به دانش عمیق و تسلط بر مباحث مورد نظر دارند و لازم است که از منابع مناسبی مانند دوره نکته و تست و پلتفرم آزمون استفاده کنند.
چه روشهایی برای دسترسی به جواب تشریحی کنکور کامپیوتر ۱۴۰۲ وجود دارد؟
دو روش: (۱) پلتفرم آزمون (۲) دورههای نکته و تست
چگونه به کلید کنکور ارشد کامپیوتر ۱۴۰۲ دسترسی داشته باشم؟
میتوانید کلید کنکور ارشد کامپیوتر ۱۴۰۲ و سایر کنکورها را از صفحه دفترچههای کنکور ارشد کامپیوتر که در بالا معرفی کردیم، دانلود نمایید.

اشتراکhttps://www.konkurcomputer.ir/b509



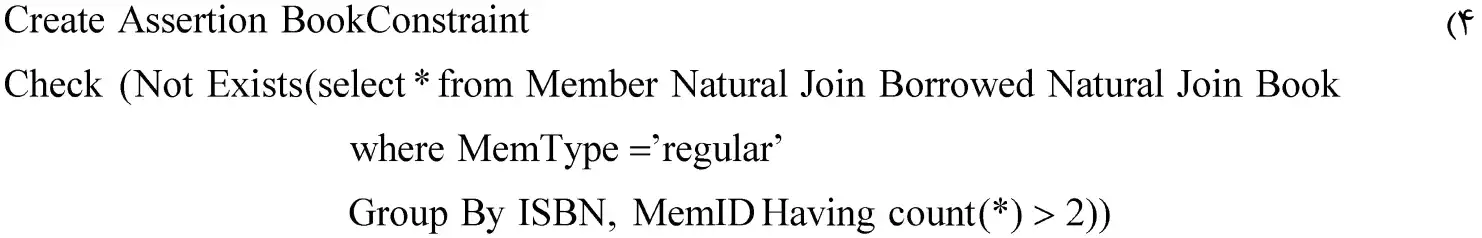
 در این صفحه تمامی دروس رشته کامپیوتر بطور کامل معرفی شده است، همچنین سرفصل هر یک از این دروس و منابع آن نیز برای شما عزیزان معرفی شده است میتوانید به پاسخ تشریحی تمامی تستهای کنکور، از اولین سال برگزاری دسترسی داشته باشید. علاوه بر روش سنتی حل تستها، روشهایی بیان میشود که با استفاده از آنها میتوان بسیاری از تستها را در زمان کمتری حل کرد.
در این صفحه تمامی دروس رشته کامپیوتر بطور کامل معرفی شده است، همچنین سرفصل هر یک از این دروس و منابع آن نیز برای شما عزیزان معرفی شده است میتوانید به پاسخ تشریحی تمامی تستهای کنکور، از اولین سال برگزاری دسترسی داشته باشید. علاوه بر روش سنتی حل تستها، روشهایی بیان میشود که با استفاده از آنها میتوان بسیاری از تستها را در زمان کمتری حل کرد. از نگاه دانشجویان، قدرت بیان فوق العاده استاد رضوی و پوشش ۱۰۰ درصدی تمامی سرفصلها، نکات و تستها، ویدیوهای حل تست ساختمان داده و طراحی الگوریتم را به بهترین ویدیو حل تست کشور در درس ساختمان و الگوریتم تبدیل کرده است. این فیلم پرطرفدارترین و پرفروشترین فیلم حل تست ساختمان داده و الگوریتم کشور است و هر سال بیش از ۶۰۰۰ نفر این فیلم را تهیه میکنند
از نگاه دانشجویان، قدرت بیان فوق العاده استاد رضوی و پوشش ۱۰۰ درصدی تمامی سرفصلها، نکات و تستها، ویدیوهای حل تست ساختمان داده و طراحی الگوریتم را به بهترین ویدیو حل تست کشور در درس ساختمان و الگوریتم تبدیل کرده است. این فیلم پرطرفدارترین و پرفروشترین فیلم حل تست ساختمان داده و الگوریتم کشور است و هر سال بیش از ۶۰۰۰ نفر این فیلم را تهیه میکنند بهترین دوره نکته و تست هوش مصنوعی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست هوش و نحوه استفاده از نکته و تست هوش مصنوعی گفته شده
بهترین دوره نکته و تست هوش مصنوعی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست هوش و نحوه استفاده از نکته و تست هوش مصنوعی گفته شده دوره نکته و تست پایگاه داده و ویژگیها و اهمیت دوره نکته و تست پایگاه داده و نحوه استفاده صحیح از نکته و تست پایگاه داده کنکور ارشد کامپیوتر و آیتی در این صفحه عالی توضیح داده شده است
دوره نکته و تست پایگاه داده و ویژگیها و اهمیت دوره نکته و تست پایگاه داده و نحوه استفاده صحیح از نکته و تست پایگاه داده کنکور ارشد کامپیوتر و آیتی در این صفحه عالی توضیح داده شده است بهترین دوره نکته و تست سیستم عامل در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست سیستم های عامل و نحوه استفاده از نکته و تست سیستم عامل گفته شده
بهترین دوره نکته و تست سیستم عامل در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست سیستم های عامل و نحوه استفاده از نکته و تست سیستم عامل گفته شده بهترین دوره نکته و تست شبکه کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست شبکه های کامپیوتری و نحوه استفاده از نکته و تست شبکه گفته شده
بهترین دوره نکته و تست شبکه کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست شبکه های کامپیوتری و نحوه استفاده از نکته و تست شبکه گفته شده دوره نکته و تست نظریه زبان ها و ماشین ها در این صفحه قرار گرفته و ویژگی ها و اهمیت دوره نکته و تست نظریه زبان ها و ماشین ها بررسی شده است
دوره نکته و تست نظریه زبان ها و ماشین ها در این صفحه قرار گرفته و ویژگی ها و اهمیت دوره نکته و تست نظریه زبان ها و ماشین ها بررسی شده است دوره نکته و تست سیگنال و سیستم و ویژگیهای نکته و تست سیگنال و نحوه استفاده صحیح از نکته و تست سیگنال کنکور ارشد کامپیوتر در این صفحه عالی توضیح داده شده
دوره نکته و تست سیگنال و سیستم و ویژگیهای نکته و تست سیگنال و نحوه استفاده صحیح از نکته و تست سیگنال کنکور ارشد کامپیوتر در این صفحه عالی توضیح داده شده بهترین دوره نکته و تست مدار منطقی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست مدار منطقی و نحوه استفاده از نکته و تست مدار منطقی گفته شده
بهترین دوره نکته و تست مدار منطقی کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست مدار منطقی و نحوه استفاده از نکته و تست مدار منطقی گفته شده بهترین دوره نکته و تست الکترونیک دیجیتال کشور در این صفحه معرفی شده و اهمیت دوره نکته و تست الکترونیک دیجیتال و نحوه استفاده صحیح از دوره بیان شده است
بهترین دوره نکته و تست الکترونیک دیجیتال کشور در این صفحه معرفی شده و اهمیت دوره نکته و تست الکترونیک دیجیتال و نحوه استفاده صحیح از دوره بیان شده است بهترین دوره نکته و تست ریاضیات گسسته کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست گسسته و نحوه استفاده از نکته و تست گسسته گفته شده
بهترین دوره نکته و تست ریاضیات گسسته کشور در این صفحه معرفی و ویژگیها و اهمیت دوره نکته و تست گسسته و نحوه استفاده از نکته و تست گسسته گفته شده دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند تمامی دفترچههای کنکور کامپیوتر را بهصورت رایگان دانلود کنید.
دفترچه سوالات کنکورهای ارشد کامپیوتر از اولین سال برگزاری تا کنکور 1403 به همراه کلید نهایی سازمان سنجش در این صفحه بصورت رایگان قرار داده شده است تا بتوانید به راحتی و بدون صرف زمان زیاد برای جستجو در اینترنت، از دفترچه سوالات سالهای گذشته استفاده نمایند تمامی دفترچههای کنکور کامپیوتر را بهصورت رایگان دانلود کنید.
 ارشد کامپیوتر چیست؟
این مقاله عالی به معرفی ارشد کامپیوتر میپردازد و درباره آینده رشته کامپیوتر و نحوه اپلای کردن توضیح میدهد شامل سوالات متنوعی از جمله طراحی الگوریتمآموزش طراحی الگوریتم به زبان ساده
ارشد کامپیوتر چیست؟
این مقاله عالی به معرفی ارشد کامپیوتر میپردازد و درباره آینده رشته کامپیوتر و نحوه اپلای کردن توضیح میدهد شامل سوالات متنوعی از جمله طراحی الگوریتمآموزش طراحی الگوریتم به زبان ساده درس طراحی الگوریتم یکی از مهمترین و بنیادیترین دروس رشته کامپیوتر است. هدف از این درس، معرفی روشهای مختلف طراحی الگوریتمها برای حل مسائل گوناگون است، در این صفحه به معرفی و آموزش طراحی الگوریتم پرداخته شده است. و ساختمان دادهآموزش ساختمان داده و الگوریتم
درس طراحی الگوریتم یکی از مهمترین و بنیادیترین دروس رشته کامپیوتر است. هدف از این درس، معرفی روشهای مختلف طراحی الگوریتمها برای حل مسائل گوناگون است، در این صفحه به معرفی و آموزش طراحی الگوریتم پرداخته شده است. و ساختمان دادهآموزش ساختمان داده و الگوریتم هر ساختمان داده یک نوع فرمت ذخیرهسازی و مدیریت دادهها در کامپیوتر است، که امکان دسترسی و اصلاح کارآمد آن دادهها را برای یکسری از الگوریتمها و کاربردها فراهم میکند، در این صفحه به بررسی و آموزش ساختمان داده و الگوریتم پرداخته شده است، شبکهجامعترین آموزش درس شبکه های کامپیوتری
هر ساختمان داده یک نوع فرمت ذخیرهسازی و مدیریت دادهها در کامپیوتر است، که امکان دسترسی و اصلاح کارآمد آن دادهها را برای یکسری از الگوریتمها و کاربردها فراهم میکند، در این صفحه به بررسی و آموزش ساختمان داده و الگوریتم پرداخته شده است، شبکهجامعترین آموزش درس شبکه های کامپیوتری درس شبکه های کامپیوتری یکی از مهمترین و بنیادیترین دروس رشته کامپیوتر است، با توجه به اینکه اینترنت امروزی بزرگترین سیستم مهندسی ساخت دست بشر در تمام طول تاریخ است، آشنایی با شبکههای کامپیوتری برای تمامی علاقهمندان و دانشجویان رشته کامپیوتر الزامی است، در این راستا در این صفحه به معرفی شبکههای کامپیوتری پرداخته شده است، هوش مصنوعیدرس هوش مصنوعی
درس شبکه های کامپیوتری یکی از مهمترین و بنیادیترین دروس رشته کامپیوتر است، با توجه به اینکه اینترنت امروزی بزرگترین سیستم مهندسی ساخت دست بشر در تمام طول تاریخ است، آشنایی با شبکههای کامپیوتری برای تمامی علاقهمندان و دانشجویان رشته کامپیوتر الزامی است، در این راستا در این صفحه به معرفی شبکههای کامپیوتری پرداخته شده است، هوش مصنوعیدرس هوش مصنوعی این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده و ... است. داوطلبان برای پاسخگویی به این سوالات نیاز به دانش عمیق و تسلط بر مباحث مورد نظر دارند و لازم است که از منابع مناسبی مانند دوره نکته و تست و پلتفرم آزمون استفاده کنند.
این صفحه عالی به معرفی درس هوش مصنوعی از جمله پیش نیازهای درس هوش مصنوعی، سرفصل و منابع درس هوش مصنوعی و فیلمهای آموزشی درس هوش مصنوعی پرداخته شده و ... است. داوطلبان برای پاسخگویی به این سوالات نیاز به دانش عمیق و تسلط بر مباحث مورد نظر دارند و لازم است که از منابع مناسبی مانند دوره نکته و تست و پلتفرم آزمون استفاده کنند.










































