تبدیل مبنا 16 به 2

ابتدا مقاله به معرفی سیستم اعداد موجود در دنیای کامپیوتر پرداخته و از بین این سیستم‌های موجود سیستم‌های دودویی و هگزادسیمال را توضیح داده است که در ادامه روش تبدیل مبنا 16 به 2 و برعکس را شرح و الگوریتم تبدیل مبنا 16 به 2 را ترسیم و برنامه ی تبدیل مبنا 16 به 2 را به روش بازگشتیتوضیح تابع بازگشتی، دنباله بازگشتی و رابطه بازگشتیاین صفحه عالی به توضیح تابع بازگشتی و دنباله بازگشتی و رابطه بازگشتی پرداخته و توضیح داده تابع بازگشتی چیست و چگونه کار می کند و کاربرد توابع بازگشتی را گفته در زبان برنامه نویسی پایتون آموزش جامع پایتونپایتون فقط برای برنامه نویسان و دانشمندان داده نیست! یادگیری پایتون می‌تواند فرصت‌های جدیدی را برای کسانی که در حرفه‌های کم‌تر داده‌محوری مثل روزنامه‌نگاری، صاحبان مشاغل کوچک یا بازاریابی رسانه‌های اجتماعی هستند، ایجاد کند. و همچنین تبدیل مبنا 2 به 16 را نیز پیاده سازی کرده است.

سیستم اعداد

سیستم اعداد یک سیستم است که دارای مجموعه‌ای از اعداد، ارقام و گاهی کاراکترها است و هر کدام از آنها معنی خاصی دارند. در کامپیوترها، چهار سیستم عددی پرکاربرد وجود دارد:

1. سیستم عددی دودویی (Binary) این سیستم فقط شامل دو عدد 0 و 1 می‌باشد.
2. سیستم عددی Octal این سیستم شامل اعداد 0 تا 7 است.
3. سیستم عددی Decimal این سیستم که در زندگی روزمره ما استفاده می‌شود، ده رقم از 0 تا 9 را شامل می‌شود.
4. سیستم عددی Hexadecimal این سیستم شامل اعداد 0 تا 9 و حروف A تا F است. به عنوان مثال، کاراکتر “F” در این سیستم معادل عدد 15 در سیستم عددی دهدهی است.

هر یک از این سیستم‌ها برای کاربردهای خاصی طراحی شده‌اند. برای مثال، سیستم دودویی مبنای اصلی زبان های برنامه نویسیزبان های برنامه نویسی چیست؟این مقاله عالی توضیح داده که زبان های برنامه نویسی چیست؟ و انواع زبان های برنامه نویسی و بهترین زبان برنامه نویسی برای شروع و پردرآمدترین آنها را معرفی کرده و کامپیوترها است که در این مقاله تبدیل مبنا از 16 به 2 را یاد خواهیم گرفت.

سیستم عددی دودویی (2)

سیستم عددی دودویی یا باینری، یک سیستم است که فقط از دو رقم 0 و 1 استفاده می‌کند. این سیستم به عنوان مبنای اصلی برای زبان‌ های برنامه‌ نویسی و کامپیوترها شناخته می‌شود.

در این سیستم، هر موقعیت در یک عدد دودویی نشان‌دهنده قدرت 0 پایه (2) است. به عنوان مثال، اگر یک عدد دودویی را در نظر بگیریم، آخرین موقعیت در این عدد نشان‌دهنده قدرت x پایه (2) است. به عنوان مثال، اگر x را برابر با 3 در نظر بگیریم، مقدار این موقعیت برابر با 2 به توان 3 یا 8 خواهد بود.

سیستم عددی هگزادسیمال (16)

سیستم عددی هگزادسیمال یا Hexadecimal، سیستمی است که بر پایه 16 می‌باشد. این سیستم از نمادهای 0 تا 9 برای مقادیر صفر تا نه و از حروف A, B, C, D, E, F برای مقادیر ده تا پانزده استفاده می‌کند. این سیستم به دلیل فرمت تقریباً فشرده‌ای که دارد، گزینه‌ مناسبی برای نمایش رشته‌های باینری طولانی به شمار می‌رود و درک آن نسبت به رشته‌های باینری متشکل از صفر و یک‌ها آسان‌تر است. هر رقم هگزادسیمال، نشان‌دهنده چهار رقم دودویی (بیت) است. برای تبدیل اعداد دودویی به هگزادسیمال، می‌توان اعداد باینری را به گروه‌های 4 بیتی تقسیم کرد و هر گروه 4 بیتی را به یک رقم هگزادسیمال تبدیل کرد.

تبدیل مبنای 16 به 2

برای تبدیل یک عدد از مبنای 16 به 2 نیاز به 4 بیت است ، می توان از روش زیر استفاده کرد:

1. هر رقم از عدد مبنای 16 را به تنهایی در نظر بگیرید.
2. هر رقم را به مبنای 2 تبدیل کنید. به عنوان مثال، اگر رقم 7 باشد، در مبنای 2 به صورت 0111 خواهد بود.
3. این کار را برای تمام ارقام انجام دهید و نتایج را پشت‌سرهم قرار دهید.

به‌عنوان‌مثال، اگر عدد مبنای 16 شما 2A3 باشد، تبدیل مبنا 16 به 2 به این صورت خواهد بود:

• 2 در مبنای 16 به مبنای 2 تبدیل می شود 0010
• A در مبنای 16 به مبنای 2 تبدیل می شود 1010
• 3 در مبنای 16 به مبنای 2 تبدیل می شود 0011

بنابراین، تبدیل مبنا 16 به 2 :2A3 در مبنای 16 به 001010100011 در مبنای 2 می باشد.

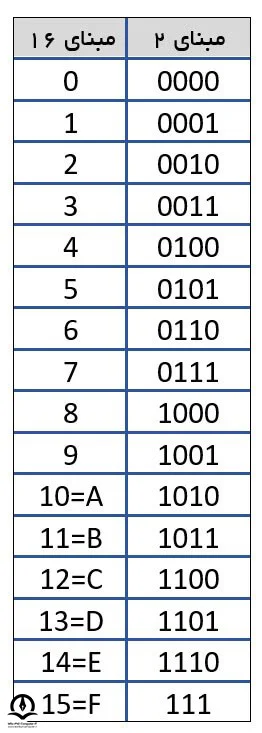
تبدیل مبنا 2 به 16

1. عدد مبنای 2 را به گروه های 4 بیتی تقسیم کنید. اگر تعداد بیت ها بر 4 بخش پذیر نبود، می توانید از صفر (0) برای پر کردن بیت های اضافی در سمت چپ استفاده کنید.
2. هر گروه 4 بیتی را به تنهایی در نظر بگیرید و آن را به مبنای 16 تبدیل کنید. به عنوان مثال، اگر گروه 4 بیتی 1010 باشد، در مبنای 16 به صورت A خواهد بود.
3. این کار را برای تمام گروه‌های 4 بیتی انجام دهید و نتایج را پشت سر هم قرار دهید.

به‌عنوان‌مثال، اگر عدد مبنای 2 شما 110101011 باشد، تبدیل به مبنای 16 به این صورت خواهد بود:

1. ابتدا عدد را به گروه‌های 4 بیتی تقسیم می کنیم: 0110 1010 11
2. سپس هر گروه را به مبنای 16 تبدیل می کنیم:

• 0110 در مبنای 2 به مبنای 16 تبدیل می شود 6
• 1010 در مبنای 2 به مبنای 16 تبدیل می شود A
• 0011 در مبنای 2 به مبنای 16 تبدیل می شود 3

بنابراین، 110101011 در مبنای 2 به 6A3 در مبنای 16 تبدیل می شود.

الگوریتم تبدیل مبنا 16 به 2

الگوریتم تبدیل مبنا 16 به 2 یک عدد هگزادسیمال را به عدد باینری تبدیل می‌کند. اینجا چگونگی کارکرد آن توضیح داده شده است:

1. ابتدا یک دیکشنری به نام mapping تعریف می‌کنیم که هر رقم هگزادسیمال (از 0 تا F) را به معادل باینری 4 بیتی آن نگاشت می‌کند.
2. سپس یک‌رشته خالی به نام binary_number تعریف می‌کنیم تا عدد باینری نهایی را در آن ذخیره کنیم.
3. با استفاده از یک حلقه برای، هر رقم از عدد هگزادسیمال ورودی را بررسی می‌کنیم. برای هر رقم، معادل باینری 4 بیتی آن را از دیکشنری mapping پیدا کرده و به انتهای رشته binary_number اضافه می‌کنیم.
4. در نهایت، تابع عدد باینری نهایی را برمی‌گرداند

def hex_to_bin(hex_number):
#مپ کردن هر رقم هگزادسیمال به معادل باینری 4 بیتی آن
mapping = {
'0': '0000' , '1': '0001' , '2': '0010' , '3': '0011',
'4': '0100' , '5': '0101' , '6': '0110' , '7': '0111',
'8': '1000' , '9': '1001' , 'A': '1010' , 'B': '1011',
'C': '1100' , 'D': '1101' , 'E': '1110' , 'F': '1111',
}
binary_number = ''
for digit in hex_number:
binary_nimber += mapping[digit.upper()]
return binary_nimber

#مثال استفاده از تابع
binary_nimber ='2A3'
print(f'Binary representation of {hex_number} is {hex_to_bin(hex_number)}')

def hex_to_bin(hex_number):
#مپ کردن هر رقم هگزادسیمال به معادل باینری 4 بیتی آن
mapping = {
'0': '0000' , '1': '0001' , '2': '0010' , '3': '0011',
'4': '0100' , '5': '0101' , '6': '0110' , '7': '0111',
'8': '1000' , '9': '1001' , 'A': '1010' , 'B': '1011',
'C': '1100' , 'D': '1101' , 'E': '1110' , 'F': '1111',
}
binary_number = ''
for digit in hex_number:
binary_nimber += mapping[digit.upper()]
return binary_nimber

#مثال استفاده از تابع
binary_nimber ='2A3'
print(f'Binary representation of {hex_number} is {hex_to_bin(hex_number)}')

کپی کردن کد

برنامه تبدیل مبنا 16 به 2 به روش بازگشتی

تابع بازگشتی برای تبدیل یک عدد هگزادسیمال به باینری در زبان برنامه‌ نویسی پایتون:

def hex_to_bin_recursive(hex_number):
mapping = {
'0': '0000' , '1': '0001' , '2': '0010' , '3': '0011',
'4': '0100' , '5': '0101' , '6': '0110' , '7': '0111',
'8': '1000' , '9': '1001' , 'A': '1010' , 'B': '1011',
'C': '1100' , 'D': '1101' , 'E': '1110' , 'F': '1111',
}

if len(hex_number) == 1:
return mapping[hex_number.upper()]
else:
return hex_to_bin_recursive(hex_number[:-1]) + mapping[hex_number[:-1].upper()]

#مثال استفاده از تابع
hex_nimber ='2A3'
print(f'Binary representation of {hex_number} is {hex_to_bin_recursive(hex_number)}')

def hex_to_bin_recursive(hex_number):
mapping = {
'0': '0000' , '1': '0001' , '2': '0010' , '3': '0011',
'4': '0100' , '5': '0101' , '6': '0110' , '7': '0111',
'8': '1000' , '9': '1001' , 'A': '1010' , 'B': '1011',
'C': '1100' , 'D': '1101' , 'E': '1110' , 'F': '1111',
}

if len(hex_number) == 1:
return mapping[hex_number.upper()]
else:
return hex_to_bin_recursive(hex_number[:-1]) + mapping[hex_number[:-1].upper()]

#مثال استفاده از تابع
hex_nimber ='2A3'
print(f'Binary representation of {hex_number} is {hex_to_bin_recursive(hex_number)}')

کپی کردن کد

این تابع با استفاده از روش بازگشتی، هر رقم از عدد هگزادسیمال ورودی را به معادل باینری 4 بیتی آن تبدیل می‌کند. اگر عدد هگزادسیمال فقط یک رقم داشته باشد، تابع معادل باینری آن را برمی‌گرداند. در غیر این صورت، تابع خودش را با بخشی از عدد هگزادسیمال که شامل همه رقم‌ها به جز آخرین رقم است، فراخوانی می‌کند و سپس معادل باینری آخرین رقم را به نتیجه اضافه می‌کند.

برنامه تبدیل مبنا 2 به 16 به روش بازگشتی

تابع بازگشتی در زبان برنامه‌ نویسی پایتون برای تبدیل مبنا 2 به 16 به روش بازگشتی:

def bin_to_hex_recursive(binary_number):
mapping = {
'0': '0000' , '1': '0001' , '2': '0010' , '3': '0011',
'4': '0100' , '5': '0101' , '6': '0110' , '7': '0111',
'8': '1000' , '9': '1001' , 'A': '1010' , 'B': '1011',
'C': '1100' , 'D': '1101' , 'E': '1110' , 'F': '1111',
}

if len(binary_number) == 4:
return mapping[binary_number]
else:
return bin_to_hex_recursive(binary_number[:-4]) + mapping[binary_number[:-4]]

#مثال استفاده از تابع
binary_nimber ='001010100011'
print(f'Hexadecimal representation of {binary_nimber} is {bin_to_hex_recursive(binary_nimber)}')

def bin_to_hex_recursive(binary_number):
mapping = {
'0': '0000' , '1': '0001' , '2': '0010' , '3': '0011',
'4': '0100' , '5': '0101' , '6': '0110' , '7': '0111',
'8': '1000' , '9': '1001' , 'A': '1010' , 'B': '1011',
'C': '1100' , 'D': '1101' , 'E': '1110' , 'F': '1111',
}

if len(binary_number) == 4:
return mapping[binary_number]
else:
return bin_to_hex_recursive(binary_number[:-4]) + mapping[binary_number[:-4]]

#مثال استفاده از تابع
binary_nimber ='001010100011'
print(f'Hexadecimal representation of {binary_nimber} is {bin_to_hex_recursive(binary_nimber)}')

کپی کردن کد

این تابع با استفاده از روش بازگشتی، هر 4 بیت از عدد باینری ورودی را به معادل هگزادسیمال آن تبدیل می‌کند. اگر عدد باینری فقط 4 بیت داشته باشد، تابع معادل هگزادسیمال آن را برمی‌گرداند. در غیر این صورت، تابع خودش را با بخشی از عدد باینری که شامل همه بیت‌ها به جز 4 بیت آخر است، فراخوانی می‌کند و سپس معادل هگزادسیمال 4 بیت آخر را به نتیجه اضافه می‌کند.

جمع‌بندی

دانستیم که چهار سیستم عددی پرکاربرد وجود دارد که از بین آنها سیستم عددی دودویی و سیستم عددی هگزادسیمال معرفی شده‌اند. سیستم عددی دودویی یا باینری، یک سیستم است که فقط از دو رقم 0 و 1 استفاده می‌کند. در این سیستم، هر موقعیت در یک عدد دودویی نشان‌دهنده قدرت 0 پایه (2) است. سیستم عددی هگزادسیمال یا Hexadecimal، سیستمی است که بر پایه 16 می‌باشد. این سیستم از نمادهای 0 تا 9 برای مقادیر صفر تا نه و از حروف A, B, C, D, E, F برای مقادیر ده تا پانزده استفاده می‌کند.

برای تبدیل یک عدد از مبنا 16 به 2 نیاز به 4 بیت است که هر رقم از عدد مبنای 16 را به تنهایی در نظر بگیرید.هر رقم را به مبنای 2 تبدیل کنید. این کار را برای تمام ارقام انجام دهید و نتایج را پشت سر هم قرار دهید. برای تبدیل مبنا 2به 16 هر گروه 4 بیتی را به تنهایی در نظر بگیرید و آن را به مبنای 16 تبدیل کنیدو در ادامه هم با برنامه تبدیل مبنا 16 به 2 به روش بازگشتی در زبان برنامه نویسی پایتون آشنا شدیم.

مطالب مرتبط

همه مقالات

مدار منطقی

رم کامپیوتر چیست؟ رم کجاست؟ معرفی انواع رم (RAM) کامپیوتر

تبدیل مبنا 10 به 2

معرفی گرایش معماری کامپیوتر مقطع ارشد دانشگاه شهید بهشتی