به بیانی ساده می توان گفت در ریاضیات گسسته تعداد نقاط بین دو نقطه مشخص، واضح و معین است در حالی که در ریاضیات پیوسته، بین دو نقطه مشخص تعداد بی نهایتی نقطه دیگر وجود دارد. به عبارت دیگر درریاضیات گسسته، شما با مقادیر مشخص کار می کنید اما ریاضیات پیوسته بر پایه اعداد پیوسته بنا شده است. برخلاف ریاضیات پیوسته که مقادیر آن ها به آرامی تغییر می کند، سرعت تغییر در مقادیر مورد مطالعه در ریاضی گسسته (مانند اعداد صحیح ، نمودارها و عبارات منطقی) بسیار بالاست.
به عبارت دیگر می توان گفت هر زمان اشیا شمارش می شوند، روابط بین مجموعه های متناهی (یا قابل شمارش) مورد مطالعه قرار می گیرد و بطور کلی در فرایندهایی که شامل تعداد محدودی از مراحل هستند، از ریاضیات گسسته یا Discrete Mathematics استفاده می شود.

از جمله دلایل اهمیت روز افزون آموزش ریاضیات گسسته ذخیره و دستکاری اطلاعات به صورت گسسته توسط ماشین های محاسباتی است.
در ادامه مطلب هر آن چه برای آموزش درس ریاضی گسسته، منابع، مراجع و کاربردهای آن نیاز دارید در اختیار شما قرار می گیرد.
ریاضیات گسسته چیست؟
ریاضی گسسته (Discrete Mathematics) بخشی از ریاضیات است که به مطالعه اشیاء گسسته اختصاص دارد. (در اینجا گسسته به معنای عناصر متمایز یا غیر مرتبط است).
به عنوان یکی از اصلی ترین دروس رشته کامپیوتر در مقاطع کارشناسی و کارشناسی ارشد، دانش ساختمان گسسته می تواند به ما در یافتن راه حل بسیاری از مشکلات حوزه کامپیوتر و آی تی کمک کند و این موضوع بیانگر ضرورت هرچه بیشتر آشنایی با کاربردهای مبانی گسسته در کامپیوتر است.
تاریخچه ریاضیات گسسته شامل مشکلات چالش برانگیزی بوده است که توجه های زیادی را متوجه این حوزه کرده است.
بعنوان مثال در تئوری گراف، تحقیقات بسیاری در تلاش برای اثبات قضیه چهار رنگ صورت گرفت
قضیه چهار رنگ بیان میکند که : برای رنگ آمیزی نقشه ای حاوی کشورها حداکثر به 4 رنگ نیاز داریم، به طوریکه که هیچ دو کشور مجاوری همرنگ نباشد
گمان درستی این قضیه برای اولین بار در 23 اکتبر 1852 مطرح شد، هنگامی که فرانسیس گاتری (Francis Guthrie)، در حالی که سعی در رنگ آمیزی نقشه شهرهای انگلیس را داشت، متوجه شد که فقط به چهار رنگ مختلف برای اینکار نیاز است. این مسله برخلاف ظاهر ساده اش سال ها فکر دانشمندان را به خود مشغول کرده بود، علی رغم تمام تلاش هایی که طی سال های 1852 تا 1976 برای اثبات این قضیه صورت می گرفت، همه آن ها به بن بست می رسیدند. سر انجام این قضیه در 21 ژوئن سال 1976 توسط کنت اپل و ولفگانگ هاکن از دانشگاه ایلینوی با استفاده از کامپیوتر اثبات و در اعلامیه ای بیان شد. این اولین قضیه بزرگ و مهمی بود که با استفاده از کامپیوتر اثبات شد و اعلامیه اپل و هاکن توسط رسانه های خبری سراسر جهان به طور گسترده ای گزارش شد. در ابتدا، این اثبات توسط همه ریاضیدانان پذیرفته نشد، زیرا برای انسان ممکن نبود تا بتواند درستی یک اثبات با کمک رایانه را به صورت دستی بررسی کند.
اثبات کنت اپل و ولفگانگ هاکن بی نهایت نقشه های احتمالی را به 1482 کاهش میداد که باید یکی یکی توسط رایانه بررسی میشد و بیش از هزار ساعت طول میکشید.

ویدیو درس ریاضیات گسسته
بهوقت بهار تا ۳ اردیبهشت
35%
ویدیو نکته و تست ریاضیات گسسته
بهوقت بهار تا ۳ اردیبهشت
35%انواع مشکلات حل شده با استفاده از ریاضیات گسسته عبارتند از:
شما در درس ریاضیات گسسته ساختارهای گسسته و تکنیکهای مورد نیاز برای حل مشکلاتی از این قبیل را یاد خواهید گرفت:
- چند روش برای انتخاب رمز ورود معتبر در یک سیستم کامپیوتری وجود دارد؟
- احتمال برنده شدن در یک قرعه کشی چقدر است؟
- آیا لینکی بین دو کامپیوتر در شبکه وجود دارد؟
- چگونه می توان پیام های ایمیل های اسپم را شناسایی کرد؟
- چگونه می توانیم پیامی را رمزگذاری کنیم تا هیچ گیرنده که ما نمیخواهیم به عمد نتواند آن را بخواند؟
- کوتاهترین مسیر بین دو شهر با استفاده از سیستم حمل و نقل چیست؟
- چگونه می توان لیستی از اعداد صحیح را به ترتیب صعودی مرتب کرد؟
- چند مرحله برای انجام چنین مرتب سازی لازم است؟
- چگونه می توان ثابت کرد که یک الگوریتم مرتب سازی به درستی یک لیست را مرتب می کند؟
- چگونه می توان مداری طراحی کرد که دو عدد صحیح را جمع کند؟
- چند آدرس اینترنتی معتبر وجود دارد؟
چرا باید ریاضیات گسسته را مطالعه کنید؟
چندین دلیل مهم برای مطالعه ریاضیات گسسته وجود دارد.
اول، از طریق یادگیری ریاضیات گسسته می توانید بلوغ ریاضی خود را توسعه دهید: یعنی توانایی شما در درک و ایجاد استدلال های ریاضی افزایش پیدا میکند. بدون این مهارت ها در تحصیلات خود در علوم ریاضی به مشکل بر خواهید خورد
دوم، ریاضیات گسسته دروازه ورود به دوره های پیشرفته تر در تمام بخشهای علوم ریاضی است. ریاضیات گسسته مبانی ریاضی بسیاری از دوره های علوم کامپیوتر از جمله ساختمان داده ها، طراحی الگوریتم ها، تئوری پایگاه داده، تئوری اتوماتها (automata theory)، زبان های فرمال، نظریه کامپایلر (compiler theory)، امنیت رایانه و سیستم عامل ها است. در صورتی دانشجویان مبانی ریاضی مناسبی از ریاضیات گسسته نداشته باشند این درک دروس برای آنها بسیار دشوارتر خواهد بود. در واقع دانشجویان در همه دروس مربوط به علوم کامپیوتر از مطالب مربوط به ریاضیات گسسته استفاده میکنند.
همچنین، ریاضیات گسسته شامل پیش زمینه ریاضی لازم برای حل مسائل در تحقیقات عملیاتی (شامل بسیاری از تکنیک های بهینه سازی گسسته)، شیمی، مهندسی، زیست شناسی و غیره است. بسیاری از دانشجویان، درس ریاضیات گسسته مقدماتی را بسیار چالش برانگیز تر از درس های گذشته خود، یا درس هایی که در گذشته گذرانده اند، می دانند. زیرا یکی از مهمترین اهداف این درس، آموزش توانایی استدلال و حل مسائل ریاضی است، نه فقط مجموعه ای از مهارت های گسسته. ریاضیات گسسته، با پیشرفت عصر رایانه، اهمیت بیشتری پیدا کرده است. رایانه دیجیتال اساساً یک ساختار محدود است و بسیاری از خصوصیات آن در چارچوب سیستم های ریاضی محدود قابل درک و تفسیر است.
کاربردهای درس ریاضیات گسسته
غالباً گفته می شود که ریاضیات در حل انواع مشکلات عملی مفید است و دانشمندان در حل این مسائل بر روی ریاضیات گسسته تمرکز می کنند. به طوری که بیشتر محاسباتی که انجام می شود، چه در دانشگاه و چه در صنعت، زیر مجموعه ریاضیات گسسته است. اما وقتی می گویند ریاضیات گسسته قابل استفاده است ، منظور واقعی چیست؟ چه مشکلی حل می شود؟
ریاضی باینری در واقع ریاضیات گسسته است. پس اساس وجود کامپیوتر به ریاضیات گسسته وابسته است. نرم افزارها و فایلها هر دو به عنوان رشته های عظیمی از 1 و 0 ذخیره می شوند. به همین ترتیب شبکه های کامپیوتری نیز بر اساس ریاضیات گسسته توسعه یافته اند. تئوری نمودار در توالی DNA استفاده می شود.
سیم بندی های یک کامپیوتر معمولی خانگی با استفاده از کمترین میزان کابل ، در حقیقت مسئله درخت کم وزن است. گوگل مپ نیز از طرح چنین مسئله ای برای یافتن کوتاه ترین مسیر بهره می برد. در برنامه ریزی مسیر راه آهن از ریاضی گسسته استفاده می کند. تصمیم گیری در مورد نحوه گسترش خطوط ریلی قطار، برنامه ریزی و زمانبندی قطارها و حتی برنامه ریزی برای خدمه و تجهیزات برای سفرهای قطار، نیز از تئوری نمودار و از جبر خطی توأمان استفاده می کند. بدین ترتیب متوجه می شویم که ریاضیات گسسته بخش جدا نشدنی از زندگی روزمره ما است.
مباحث و موضوعات موجود در ریاضیات گسسته
علوم تئوری کامپیوتر (Theoretical computer science)
تئوری اطلاعات (Information theory)
منطق (Logic)
تئوری (Set theory)
ترکبیات (Combinatorics)
تئوری گراف (Graph theory)
احتمالات (Probability)
تئوری اعداد (Number theory)
ساختارهای جبری (Algebraic structures)
حساب دیفرانسیل و انتگرال گسسته یا تحلیل گسسته (discrete calculus or discrete analysis)
هندسه (Geometry)
نظریه بازی ، تئوری تصمیم (Game theory, decision theory)
ریاضیات گسسته و پیوسته ترکیبی (Hybrid discrete and continuous mathematics


درس ریاضی گسسته در کنکور کارشناسی
در رشته ریاضی سوالات تخصصی به 3 دسته ریاضیات، فیزیک و شیمی تقسیم میشود، گروه علوم ریاضی 3 زیر گروه دارد و ضریب دروس کنکور ریاضی در هر زیر گروه متفاوت است، اما در هر سه زیر گروه ریاضیات دارای بیشترین ضریب هستند. 55 تست ریاضی در رشته ریاضی مطرح میشود، دروس ریاضیات شامل دروس دیفرانسیل و ریاضی پایه، هندسه تحلیلی، ریاضیات گسسته، جبروآمار و مدل سازی هست.
از درس ریاضی گسسته 15 تست مطرح میشود که نسبت به حجم مطالب تعداد تست زیادی را به خودش اختصاص داده است و بنابراین از اهمیت زیادی برخوردار است. مباحثی که از درس ریاضی گسسته در کنکور سراسری مطرح میشود به قرار زیر است: ترکیبات و آنالیز ترکیبی، احتمال، استدلال ریاضی، مجموعه ها، ضرب دکارتی و رابطه، گراف، نظریه اعداد، آمار و مدلسازی.
فیلمهای ریاضی گسسته کنکور کامپیوتر بسیار جامع است بطوری که برای داوطلبان کنکور سراسری نیز بسیار عالی است.
ریاضی گسسته در کنکور ارشد کامپیوتر
بخش ریاضیات در رشته مهندسی کامپیوتر دارای ضریب 2 است و شامل 4 درس، ریاضی 1و2، آمار و ریاضیات گسسته است، هنوز مشخص نیست که از گسسته چند تست در کنکور ارشد مطرح میشود ولی حدس ما این است که 6 تست در از این درس در کنکور ارشد کامپیوتر مطرح شود، همین طور گسسته از دورس مشترک رشته فناوری اطلاعات با ضریب ۴ است که تعداد ۶ سوال از آن مطرح میشود.
درس گسسته یک از دروس گسترده در کنکور ارشد مهندسی کامپیوتر و فناوری اطلاعات است، گستردگی درس ریاضیات گسسته به حدی است که دانشجویان نمیتوانند به تنهایی این درس را بخوانند و از پس آن بر بیایند. درس ریاضی گسسته، پایهی تمام ریاضیات کنکور ارشد است و پیش نیاز بسیاری از دروس کنکور است و از این حیث جایگاه ویژهای دارد و یکی از مهمترین دروس کنکور ارشد مهندسی کامپیوتر و آی تی محسوب میشود. و کنار گذاشتن آن اصلا توصیه نمیشود. با کنار گذاشتن درس ریاضی گسسته نه تنها قادر به زدن تستهای درس گسسته نخواهید بود بلکه به درسهای دیگرتان نیز آسیبهای جدی ای وارد میکنید.
مراجع درس ریاضی گسسته
مرجع اصلی که برای ریاضیات گسسته در دانشگاههای معتبر تدریس میشود کتاب گریمالدی است، همچنین کتابهای رزن (Rosen) و لیپزشوتز(Lipschutz) نیز در برخی از دانشگاههای ایران و جهان تدریس میشود، که میتوانید به راحتی این کتابها را در زیر دانلود کنید. برای دانلود سایر کتاب های مرجع رشته کامپیوتر به قسمت دانلود کتابهای زبان اصلی رشته کامپیوتر مراجعه کنید.
البته خواندن کتابهای رفرنس را به دانشجویان ترمهای پایینتر توصیه میکنیم نه به دانشجویانی که قصد شرکت در کنکور ارشد کامپیوتر یا فناوری اطلاعات را دارند، دلیل این امر نیز در قسمت پاسخ به سوالات متداول داوطلبان پیرامون کنکور ارشد کامپیوتر چندین بار بیان شده است که میتوانید به آن قسمت رجوع کنید. دانشجویانی که قصد دارند برای کنکور ارشد و یا دکتری کامپیوتر این درس مهم را بخوانند، میتوانند از منابعی که در قسمت معرفی منابع ارشد کامپیوتر 1401 معرفی شده استفاده کنند.
دانلود کتاب های مرجع درس ریاضیات گسسته
فصلهای ریاضیات گسسته
سر فصل مطالبی که در درس ریاضیات گسسته گفته میشود بصورت زیر است: مبانی منطق ریاضی، شمارش، روابط بازگشتی، رابطهها، تابع، مجموعه، پاست، لاتیس، گراف، نظریه اعداد، ریز موارد این فصول را در زیر میتوانید ببینید:
- گزاره نماها، سورها، اصول استنتاج
- روشهای اثبات
- توابع یک به یک و پوشا، ترکیب توابع، معکوس توابع توابع، دنبالهها
- ضرایب دوجملهای، جایگشتها و ترکیبهای با تکرار
- اصول طرد و شمول، توزیع اشیا درون جعبهها
- اصل لانه کبوتری
- متغیرهای تصادفی، امید ریاضی، واریانس
- حل روابط بازگشتی همگن و ناهمگن
- رابطههای هم ارزی، بستارها
- مشبکهها، جبر بول، خواص جبر بول
- مسیرها و همبندی، مسیرهای اویلری و همیلتونی
- گرافهای مسطح، قضیه اویلر، رنگ آمیزی گرافها
- اعداد اول، قضیه اویلر، مقدمهای بر نظریه رمزنگاری
- استقرای قوی، استقرای ساختاری
برای مشاهده اهمیت هر فصل در کنکور ارشد کامپیوتر و آی تی و اینکه در سالهای اخیر از هر فصل چه تعداد تست مطرح شده میتوانید به لینکهای زیر رجوع کنید:
بودجهبندی سوالات کنکور ارشد مهندسی کامپیوتر
بودجهبندی سوالات کنکور ارشد فناوری اطلاعات
برای نشان دادن اهمیت این درس همین بس که در مورد چند فصل ریاضیات گسسته توضیحاتی بدهیم: «فصل شمارش» در ریاضی گسسته از مهمترین فصول در کارشناسی ارشد، در کنکور کامپیوتر تقریبا همیشه دو تست بصورت مستقیم از مبحث شمارش (یکی در گسسته و یکی در آمار) میآید و در بسیاری از درسها نظیر ساختمان داده و طراحی الگوریتم، آمار و احتمال، معماری کامپیوتر، مدار منطقی، شبکه های کامپیوتری و ... از مبحث شمارش استفاده میشود و برای حل بسیاری نیاز دارید که به مبحث شمارش مسلط باشید. از «فصل بازگشتیها» فصل سوم ریاضی گسسته، در کنکور ارشد، دو تست بصورت مستقیم مطرح میشود. یک تست در درس ریاضیات گسسته و یک تست در درس ساختمان داده و الگوریتم. علاوه بر این دو تست، حداقل 5 تست در درسهای مختلف بصورت غیر مستقیم از این فصل وجود دارد، فصل دیگری از گسسته «فصل گراف» است که از اهمیتی بسیاری برخوردار است، از مبحث گراف هر ساله چندین تست بصورت مسقیم در گسسته و الگوریتم مطرح میشود، گرچه گراف گسسته با گراف الگوریتم تفاوتهایی دارد اما به یکدیگر وابسته هستند.
آموزش ریاضیات گسسته
درس ریاضی گسسته از دروس پایهای رشته کامپیوتر است، و پیش نیاز اکثر دروس رشته کامپیوتر محسوب میشود، همین طور این درس برای دانشجویانی که میخواهد به سمت تحقیقات و ریسرچ بروند بسیار درس مهم و کاربردی محسوب میشود. متاسفانه مشکلاتی در نحوه ارائه این درس و آموزش ریاضی گسسته در دانشگاههای کشور وجود دارد، همین طور مطالب این درس در دانشگاه های کشور بصورت کامل تدریس نمیشود و مطالبی نیز که مطرح میشود بعضا بصورت کامل و با جزییات بالا تدریس نمیشود، این مشکلات باعث شده دانشجویان این درس را به خوبی فرا نگیرند و در نتیجه پایه ضعیفی در این درس داشته باشند، همچنین نحوه ارائه ضعیف و بد این درس باعث شده برخی از دانشجویان احساس کنند درس ریاضیات گسسته درس سختی است و سراغ این درس نروند، در صورتی که این درس از دروس بسیار شیرین رشته کامپیوتر محسوب میشود و همان طور که قبلا هم به آن اشاره شد علاوه بر اینکه این درس برای کنکور ارشد بسیار مهم است این درس، درس بسیار مهمی برای دانشجویانی است که میخواهند در رشته کامپیوتر بصورت آکادمیک فعالیت کنند و کارهای پژوهشی انجام بدهند. آموزش ساده و پایهای درس ریاضی گسسته باعث میشود دانشجویان رشته کامپیوتر علاقه بسیاری به این درس پیدا کنند.
به علت پایه ضعیفی که اکثر دانشجویان کامپیوتر کشور دارند هنگامیکه با کتاب های کنکور شروع به مطالعه این درس میکنند چون کتاب های کنکور همه چیز را از پایه درس نداده اند، شروع به مطالعه برایشان سخت است، به همین علت در راستای کمک به دانشجویان فیلم های جلسات ابتدایی درس مهم ریاضیات گسسته را تحت اختیار دانشجویان کشور قرار داده ایم تا دانشجویان کشور بتوانند شروعی مناسب و حرفه ای داشته باشند، سعی کنید قبل از شروع درس ریاضیات گسسته ابتدا 3 جلسه رایگان زیر را تماشا کنید و بعد از روی کتاب ها مطالعه تان را شروع کنید و یا فیلم ها را بطور کامل تهیه کنید و از روی فیلم ها ادامه دهید. این فیلم ها را میتوانید براحتی در زیر مشاهده کنید
فیلم های ریاضی گسسته که برای شروع نیاز دارید

ریاضی گسسته جلسه 1

ریاضی گسسته جلسه 2

ریاضی گسسته جلسه 3

ریاضی گسسته جلسه 4

ریاضی گسسته جلسه 5

ریاضی گسسته جلسه 6

ریاضی گسسته جلسه 7

حل سوالات گسسته جلسه 1

حل سوالات گسسته جلسه 2

حل سوالات گسسته ارشد کامپیوتر 99
برای تماشای تمامی فیلمهای دیگر ریاضیات گسسته میتوانید به لینک رو به رو مراجعه کنید: آموزش ریاضیات گسسته
نظر برخی از رتبه های برتر کنکور ارشد کامپیوتر و آی تی در مورد کیفیت فیلمها

نظر رتبه 1 کنکور ارشد کامپیوتر 1403
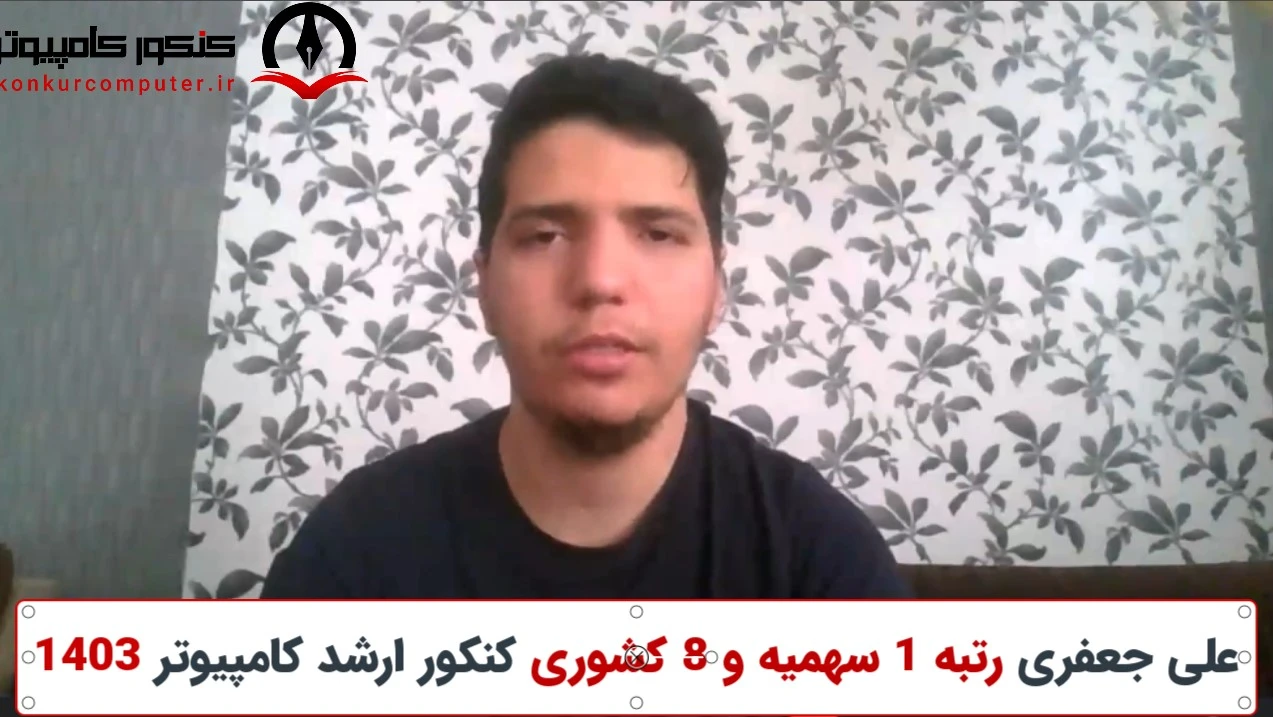
نظر رتبه 1 کنکور ارشد کامپیوتر 1403

نظر رتبه 2 کنکور ارشد کامپیوتر

نظر رتبه 1 کنکور ارشد کامپیوتر
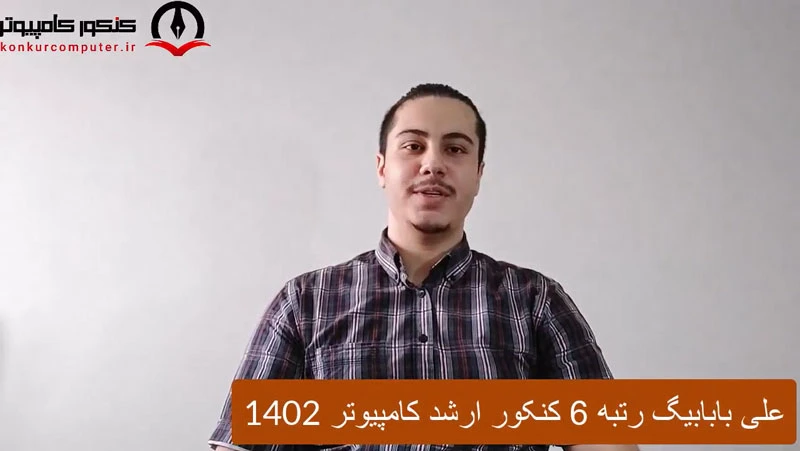
نظر رتبه 6 کنکور ارشد کامپیوتر
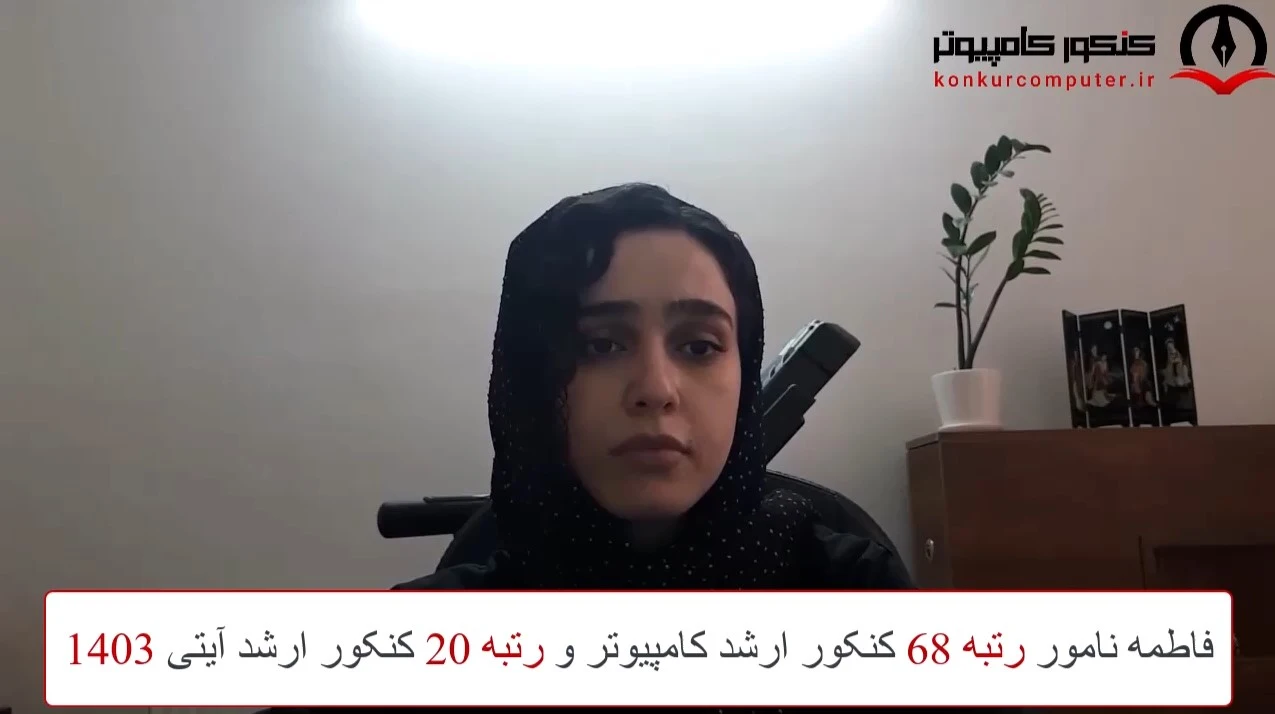
نظر رتبه 68 کنکور ارشد کامپیوتر 1403
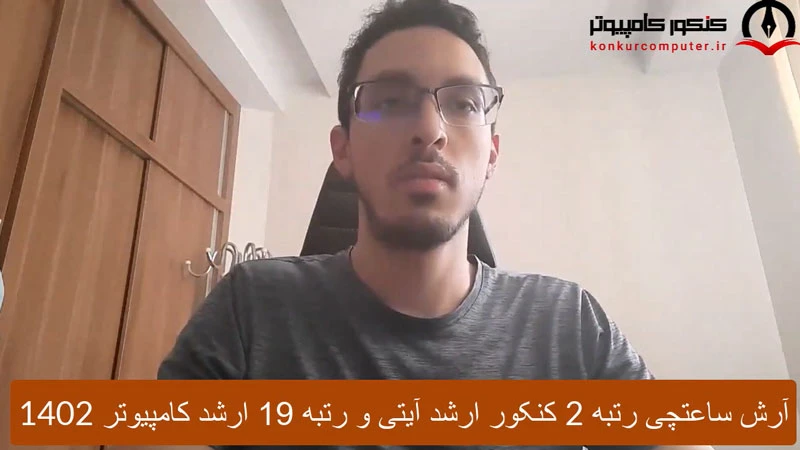
نظر رتبه 2 کنکور ارشد
نظر رتبه 6 کنکور 1400
فیلم ها خیلی قابل فهم و روان است

رتبه 9 :فیلم ها بی نقص بود

از پایه ضعیف تا شریف
نطر رتبه 10: کیفیت تدریس استاد رضوی خیلی خوبه

نظر رتبه 16: کیفیت تدریس خیلی عالی بود

جزوه کامل و ویدیوهای خیلی خوب

نحوه انتقال دانش استاد رضوی بینظیر است
ویدیوها خیلی جامع و کامل بودند
واقعا تدریس اساتید عالی بودند
نظر رتبه 8 کنکور 1400
نظر رتبه 2: معماری کامپیوتر و منطقی 100 زدم

نظر رتبه 13 کنکور ارشد کامپیوتر 1401

نظر رتبه 19: تدریس و فن بیان عالی است
نظر رتبه 12 کنکور ارشد کامپیوتر 1401
نظر رتبه 24: خیلی کامل و جامع است

فیلمها بی نظیر بود
نظر رتبه 45: کیفیت فیلم ها خوب بودن
همه دروس عالی تدریس شده بودند
نیار نیست کتاب تهیه کنید
فیلم ها با بیان شیوا و بدون ابهام بود

کیفیت بالا و هزینه مناسب

نظر رتبه 11 کنکور 1400

فیلمها بینیازم کرد

تدریس زیبا و بیان شیوا
فیلم درس و تست کافیست
فیلم های استاد رضوی از همه نظر عالی بودند

کیفیت و نحوه تدریس و قدرت بیان اساتید از همه نظر خوب بود

خیلی راضی بودم درسها خیلی عمیق تدریس میشد

از همه دروس خیلی راضی بودم
نظر پارسا شریعت
ویدیوها از نظر کیفیت عالی بودند
نظر رتبه 43 کنکور

از دروس استاد رضوی خیلی راضی بودم

نظر پیمان هاشمی

نظر رتبه 40 کنکور
تدریس از 0 تا 100
فیلم شما را جلو میاندازد
نظر رتبه 50 کنکور 1400

نظر رتبه 67 کنکور 1400

نظر ریحانه حسین زاده
نظر مرتضی اکبری

نظر رتبه 113 کنکور 1400
تاثیر منابع خوب
نظر سامان حسینی
تفاوت منابع مناسب
نظر رتبه 32 کنکور 1400

کیفیت بالا تدریس
نظر شیوا رضازاد
از روی مراجع نخوانید
فیلم ها خیلی مفهومی بودند

همه درس ها فوق العاده بود
از صفر تا صد و کامل هستند

آشنایی با استاد رضوی و کافه تدریس معجزه بود

فیلم ها جامع بودند
کل منابع من از کافه تدریس یا کنکور کامپیوتر بود
دروس واقعا فوق العاده بودند

درسها کامل و روان است
فیلم ها خیلی دقیق و جامع و کامل بودند
ویدیوها بسیار قابل فهم بودند
مطالبی که پوشش داده شده بود واقعا کامل بود

تدریس بسیار شیوا و روان و بدون ابهام
با پایه ضعیف هم فیلم ها را متوجه می شوید

فیلم ها خیلی به من کمک کرد

همه دروس را از کافه تدریس گرفتم

ویدیوهاشون خیلی به من کمک کرد
معرفی دوره درس و حل تست ریاضیات گسسته
درس ریاضیات گسسته یکی از دروس مهم و پایهای رشته کامپیوتر و همچنین پایهی تمامِ ریاضیات کنکور ارشد و همینطور پیش نیاز بسیاری از دروس کنکور است و از این حیث جایگاه ویژهای دارد و یکی از مهمترین دروس کنکور ارشد مهندسی کامپیوتر و آی تی محسوب میشود و کنار گذاشتن آن اصلا توصیه نمیشود. با کنار گذاشتن درس گسسته نه تنها قادر به زدن تستهای درس گسسته نخواهید بود بلکه به درسهای دیگرتان نیز آسیبهای جدیای وارد میکنید.
متاسفانه مشکلاتی در نحوه ارائه این درس و آموزش ریاضی گسسته در دانشگاههای کشور وجود دارد، همین طور مطالب این درس در دانشگاه های کشور بصورت کامل تدریس نمیشود، و همان مطالبی نیز که مطرح میشود بعضا بصورت کامل و با جزییات بالا تدریس نمیشود، این مشکلات باعث شده دانشجویان، این درس را به خوبی فرا نگیرند و در نتیجه پایه ضعیفی در این درس داشته باشند، همچنین نحوه ارائه ضعیف و بد این درس باعث شده برخی از دانشجویان احساس کنند درس ریاضیات گسسته درس سختی است و سراغ این درس نروند، در صورتی که این درس از دروس بسیار شیرین رشته کامپیوتر محسوب میشود.
در فیلم های ریاضیات گسسته مطالب بسیار پایهای و از 0 تا 100 و با تمامی جزییات ممکن آموزش داده میشود، آموزش ریاضی گسسته در فیلم ها بصورت اصولی و با سادهترین بیان صورت میگیرد و بر خلاف فیلمهای مشابه این فرض در نظر گرفته نشده که دانشجویان باید یکسری از مطالب را از قبل بلد باشند و همه چی از صفر توضیح داده شده است، به همین علت، تمامی دانشجویان با هر پایه و سطحی که دارند میتوانند از این فیلم بیشترین بهره را ببرند، حتی دانشجویانی که رشته لیسانس شان کامپیوتر نبوده است کاملا متوجه همه مطالب خواهند شد و درس ریاضیات گسسته را بصورت عمیق و مفهومی فرا میگیرند. در داشبورد دانشجویانی که فیلم درس ریاضیات گسسته را تهیه میکنند پی دی اف و جزوات مربوط به فیلمها نیز قرار میگیرد و دانشجویان براحتی میتوانند جزوات را پرینت بگیرند و هنگام تماشا فیلمها از جزوات خط ببرند و مطالب مهم را هایلایت کنند و همین طور اگر نیاز داشتید برای خودشان در کنار جزوات چیزی یاداشت کنند.
از نگاه دانشجویان، قدرت بیان فوق العاده استاد رضوی و پوشش ۱۰۰ درصدی تمامی سرفصلها، نکات و تستها، ویدیوهای درس ریاضیات گسسته را به بهترین ویدیو آموزشی کشور در درس ریاضیات گسسته تبدیل کرده است. در حال حاضر فیلم آموزش ریاضیات گسسته استاد رضوی پرطرفدارترین و پرفروشترین ریاضیات گسسته کشور است و هر سال بیش از ۶۰۰۰ نفر این فیلم را تهیه میکنند، آموزش ریاضیات گسسته به زبان ساده و صفر تا صد دلیل محبوبیت آموزش ریاضیات گسسته است. در فیلمهای ریاضیات گسسته تهیه شده
دانشجویان عزیز هر گونه سوالی در مورد فیلم ها دارید میتوانید از تیم پشتیبانی بپرسید:
آی دی تلگرام تیم پشتیبانی: @konkurcomputer_admin
شماره پشتیبانی: 09378555200

رامین رضوی
RAMIN RAZAVI
ایشان تا قبل از سال 94 بصورت حضوری در شهر تهران و بصورت پروازی در شهرهای مشهد، شیراز، اصفهان، گرگان و ... برای کنکور مقطع ارشد و دکتری تدریس میکردهاند، سپس در سال 94 با توجه به درخواستهای مکررِ شهرهای دیگر برای برگزاری کلاسهای آمادگی کنکور ارشد و دکتری تصمیم گرفت در جهت رفع کمبود امکانات آموزشی در شهرهای کوچک، برای اولین بار در کشور اقدام به برگزاری دورههای آموزشی آنلاین کند که ماحصل آن برقراری عدالت آموزشی طی این سالها و شرکت بیش از 24000 دانشپژوه در کلاسهای آنلاین ایشان و برگزاری 267 دوره آنلاین توسط ایشان بوده است.
در حال حاضر بیش از 90 درصد از رتبههای برتر کنکور ارشد کامپیوتر و آیتی هر سال از دانشجویان استاد رضوی هستند که این درصد موفقیت نه تنها در رشته کامپیوتر بلکه در هیچ رشته دیگری وجود نداشته است.
سرفصلهای دوره ریاضیات گسسته
برای درس ریاضیات گسسته دو فیلم زیر وجود دارد:
- فیلم درس ریاضیات گسسته
- فیلم حل سوالات و تست های ریاضیات گسسته

ویدیو درس ریاضیات گسسته
بهوقت بهار تا ۳ اردیبهشت
35%
ویدیو نکته و تست ریاضیات گسسته
بهوقت بهار تا ۳ اردیبهشت
35%در زیر سرفصلهای دوره درس و تست ریاضیات گسسته با جزئیات آورده شده است و مشخص شده است که فیلم آموزش ریاضیات گسسته و همین طور حل تست ریاضیات گسسته چند جلسه است و هر جلسه چند ساعت است و شامل چه بخشها و مباحثی است:
بخش 1
00:55'
بخش 1
1:05'اصل ضرب - حل چند مثال از اصل ضرب
بخش 2
00:40'ادامه حل مثالها از اصل ضرب
بخش 1
1:55'ادامه نکات اصل ضرب - جایگشت - انواع جایگشت - حل مثال - جایگشت در یک ردیف - جایگشت دایرهایی
بخش 2
00:45'جایگشت با تکرار - حل مثال
بخش 1
1:00'ادامه حل مثالهای جایگشت
بخش 2
00:45'دستهبندی مسائل آنالیز ترکیبی - جایگشت بدون تکرار و جایگشت با تکرار
بخش 3
1:30'فرمول جایگشت با تکرار - مسائل ترکیب - ترکیب بدون تکرار و ترکیب با تکرار - اثبات فرمول ترکیب با تکرار
بخش 1
1:20'حل مثال از مسائل ترکیب
بخش 2
1:30'خواص ترکیب (قاعدهی پاسکال، قاعدهی واندر مورد، ...) - تقسیم n شی مشابه در k سلول متمایز و حل مثال - تعداد جوابهای صحیح و نامنفی معادلهی x1 + x2 + x3 + … + xk = n
بخش 1
1:05'ادامه حل مثال از مباحث جلسه قبل
بخش 2
1:05'خواص مجموعهها در شمارش - قواعد شمول و عدم شمول
بخش 3
00:30'حل مثال
بخش 1
00:40'ادامه حل مثال از مباحث جلسه قبل
بخش 2
00:50'مسائل عدم تطبیق، ناسازگاری - حل مثال
بخش 3
1:30'تعریف تابع - تابع یک به یک - تابع پوشا - حل مثال - تعداد حالات توزیع n شی متفاوت در k سلول
بخش 1
1:40'استرلیگ نوع 1 و نوع 2 - اصل لانه کبوتری
بخش 2
1:05'حل مثال - تعمیم یافته اصل لانه کبوتری
بخش 1
1:30'شروع فصل بازگشتیها - انواع روابط بازگشتی - حل روابط بازگشتی خطی، همگن، ضریب ثابت - فرمت ریشه اعداد مختلط
بخش 2
1:25'حل روابط بازگشتی خطی، ضریب ثابت، ناهمگن
بخش 1
1:30'حل مثال از مباحث جلسه قبل - نوشتن رابطه بازگشتی برای برخی مسائل
بخش 2
1:30'ادامه نوشتن رابطه بازگشتی برای برخی مسائل
بخش 1
1:30'ادامه نوشتن رابطه بازگشتی برای برخی مسائل - تابع مولد
بخش 2
1:55'حل مثال از تابع مولد - بسط نیوتن - تعمیم بسط نیوتن - حل روابط بازگشتی با استفاده از تابع مولد
بخش 1
1:35'روش کرامر - اعداد کاتالان - مسائلی که جواب آنها کاتالان است
بخش 2
1:30'مسائلی که جواب آنها کاتالان است - رابطه بازگشتی کاتالان
بخش 1
1:30'مسئله جوزف - شروع فصل روابط - تعریف ضرب دکارتی - تعریف رابطه
بخش 2
1:10'خواص روابط (بازتاب، ضدبازتاب، تقارن، پادتقارن ...) - حل مثال از خواص روابط
بخش 1
1:00'حل مثال از خواص روابط
بخش 2
1:00'حل مثال از خواص روابط - عملیات روی روابط - عملگر not - عملگر معکوس - عملگر اجتماع
بخش 3
00:35'عملگر اشتراک - عملگر تفاضل
بخش 1
1:20'رابطهی همارزی - افراز
بخش 2
1:15'رابطهی همنهشتی - ترکیب روابط - گراف روابط - بیان ریاضی خواص روابط
بخش 1
1:25'بستارها - نکاتی در رابطه با بستارها - ماتریس روابط
بخش 2
1:00'ماتریس روابط - رابطهی سازگاری - تعریف تابع
بخش 1
1:40'رابطهی ترتیب (ترتیب جزئی، ترتیب کامل) - نکات رابطه ترتیب - پاست (مجموعه با ترتیب جزئی) - هاس
بخش 2
1:20'حل مثال از پاست و هاس - تعریف ماکسیمال و مینیمال - تعریف ماکسیمم و مینیمم
بخش 1
1:15'تعریف کران بالا و کران پایین - کوچکترین کران بالا (LUB) و بزرگترین کران پایین (GLB) - تعریف لاتیس
بخش 2
1:30'خواص لاتیس - تعریف عضو مکمل - لاتیس مکمل پذیر
بخش 1
1:25'توزیعپذیری در لاتیس - تعریف زیر شبکه - چند قضیه مهم مبحث لاتیس - جبر بول
بخش 1
1:40'شروع گراف - گراف ساده - گراف منتظم - گراف کامل - مجموع درجات گراف
بخش 2
2:25'تعداد یالها در گراف ساده n راسی (جهتدار و غیر جهتدار ) - انواع همبندی در گراف جهتدار - دنباله درجات گراف - الگوریتم هاول - حکیمی - گراف دو بخشی
بخش 1
1:10'دو گراف ایزومورف یا یکریخت - مکمل یک گراف
بخش 2
1:20'تعریف گشت، گذر، مسیر، مدار و دور - گذر و مدار اویلری
بخش 3
1:05'چند قضیه در رابطه با گذر و مدار اویلری - مسیر و سیکل همیلتونی
بخش 4
2:10'تعداد سیکلهای همیلتونی در گراف Kn,n - رنگآمیزی گراف - آشنایی با انواع گراف (درخت، سیکل، چرخ، مکعب، نردبان) - چند جملهایی کروماتیک
بخش 1
2:00'درخت آزاد - تعداد درختهای آزاد برچسبدار - نکات درخت - زیر گراف و انواع آن - درخت پوشا
بخش 2
2:00'تعداد درختهای پوشای گراف - زیر گراف القایی - دسترس پذیری - پایگاه راس و نکات آن - تطابق (جور سازی یا Matching) - تطابق ماکزیمال و تطابق ماکزیمم - تطابق کامل
بخش 3
1:30'گرافهای مسطح - چند قضیه مهم در رابطه با گرافهای مسطح - ایزومورف و همومورف
بخش 1
1:50'حل مثال از تابع مولد - تابع مولد پیچش (convolution) - بررسی رشد کاتالان - مسائلی که جواب آنها کاتالان است
بخش 2
1:30'مسائلی که جواب آنها کاتالان است - حل رابطه بازگشتی کاتالان
بخش 1
1:00'شروع فصل اعداد - مفهوم همنهشتی - حل چند مثال از همنهشتی - قضیه فرما
بخش 2
2:00'فرمولهای یافتن باقیمانده a بر k و حل چند مثال - معادلات سیال
بخش 1
1:50'ترکیب با تکرار و بدون تکرار-– جوابهای نامعادلهی a
بخش 2
1:45'اصل عدم شمول - تعداد جوابهای معادلهx1+x2+x3+… +xk = b - به دست آوردن ضریب جملات در بسط
بخش 1
1:30'مجموعهها و خواص آنها - تعداد حالات نشستن افراد دور میز گرد
بخش 2
1:55'تعداد قطرهای یک n ضلعی - توزیع n شی در k جعبه متمایز (تعداد توابع از n عضو به k عضو)
بخش 1
1:30'اصل عدم شمول - تعداد اعضای مضرب k بین 1 تا n - مجموعهها و خواص آنها - به دست آوردن ضریب جملات در بسط
بخش 2
1:55'به دست آوردن ضریب جملات در بسط - تعداد توابع یک به یک از A به B - چند جملهایی رخی - اصل عدم شمول
بخش 1
1:30'تعداد حالات پرانتزگذاری یک عبارت ریاضی - مجموعهها و خواص آنها - تعداد توابع پوشا از A به B
بخش 2
1:35'شروع بازگشتیها - نوشتن رابطه بازگشتی برای برخی مسائل - رابطه بازگشتی قرار دادن n رخ در صفحه شطرنج n در n
بخش 3
00:05'ادامه سوال رابطه بازگشتی قرار دادن n رخ در صفحه شطرنج n در n
بخش 1
1:30'حل روابط بازگشتی خطی، ضریب ثابت و همگن (2 روش) - معادله مشخصه، جواب عمومی، جواب خصوصی
بخش 2
1:30'تابع مولد پیچش - به دست آوردن رابطه بازگشتی برای تعداد جایگشتهای صعود - نزول اعداد 1 تا n (دنباله اویلری) - تابع مولد کاتلان
بخش 3
2:10'به دست آوردن رابطه بازگشتی برای بعضی مسائل - رابطه بازگشتی تعداد افرازهای n به دقیقا k جمعوند - تابع مولد
بخش 4
1:00'به دست آوردن رابطه بازگشتی برای بعضی مسائل - ماتریس سه قطری - دترمینان ماتریس سه قطری
بخش 1
1:15'تابع مک کارتی - به دست آوردن تابع مولد
بخش 2
00:40'به دست آوردن تابع مولد
بخش 3
1:30'ساخت BST با اعداد 1 تا n - شروع فصل روابط - لاتیس توزیعپذیر - تعداد اعضای یک رابطه همارزی - رابطه وجود مسیر یا بستار تعدی
بخش 1
1:35'نکاتی در رابطه با اجتماع و اشتراک توابع - مجموعه تماما مرتب - رابطه همارزی و افراز - تعریف اعداد گویا، گنگ، حقیقی و مختلط - اعداد اعشاری مختوم و متناوب
بخش 2
1:45'تعریف اعداد گنگ به نحوی دیگر - ترکیب روابط ( RoR) - ترتیب توپولوژیکی - بررسی توابع صعودی و نزولی - تعریف مجموعههای شمارا و ناشمارا
بخش 1
1:15'رابطه همارزی و همنهشتی - بستار تعدی - بررسی همارزی بودن یک رابطه
بخش 2
1:05'ترکیب روابط - رابطه بازگشتی تعداد افرازهای یک مجموعه n عضوی
بخش 3
00:55'گراف روابط - تابع ایزومورفیسم - نمودار هاس
بخش 1
1:15'لاتیس - مجموعه جزئا مرتب و تماما مرتب - عضو ماکسیمال و عضو مینیمال - شروع فصل گراف - گراف سه بخشی گراف همیلتونی و اویلری
بخش 2
2:15'تطابق (جور سازی) - تطابق ماکزیمال - تطابق ماکزیمم - تطابق کامل - بررسی دنباله درجات گراف - تعداد نواحی در گراف - ایزومورفیسم (یکریختی) و اتومورفیزم (خود ریختی)
بخش 1
1:20'درخت کامل k تایی
بخش 2
1:15'مجموعه مستقل - مجموعه مستقل ماکسیمال - نوشتن رابطه بازگشتی برای تعداد مجموعههای مستقل در یک گراف - سیکل و مسیر همیلتونی - گراف n -بخشی کامل
بخش 3
1:30'گراف همیلتونی - رابطه تعداد دورهای همیلتونی در گراف دو بخشی کامل
بخش 4
1:05'دنباله درجات یک درخت - تعداد زیر گراف القایی - گشت در گراف - رابطه تعداد زیر گرافهای m راسی در گراف Kn
بخش 5
00:40'تعداد مسیر به طول n در گراف Qn - گذر و مدار در گراف - گذر و مدار اویلری
بخش 1
2:10'منطق گزارهها - گزاره راستگو - گزاره ارضاپذیر - استنتاج معتبر - سور عمومی - به دست آوردن تعداد مقسوم علیههای یک عدد - قضیه فرما
بخش 2
1:10'نمودار هاس - ترتیب کامل و ترتیب جزئی - تعریف خوشترتیبی - مجموعههای شمارا و ناشمارا - تعداد توابع از مجموعه A به B
بخش 3
00:50'تعداد توابع از مجموعه N به مجموعه شمارای S - همنهشتی
بخش 4
1:20'خواص مجموعهها - جواب عمومی رابطه بازگشتی - تعداد درختهای پوشای گراف - بستارها - مجموعه مستقل - یکتا بودن ترتیب توپولوژیکی - وارون یک تابع
بخش 1
00:55'مجموعهی پوشا - رابطه بازگشتی تعداد ماتریسهای متقارن n×n - تابع مولد
بخش 1
1:05'حل سوالات مهندسی و آیتی سال 98 - گزارههای همارز - سور عمومی و سور وجودی - مجموعههای شمارا و ناشمارا - رابطه هم ارزی و رابطه ترتیب - گراف مسطح - به دست آوردن جواب عمومی رابطه بازگشتی - مجموعه خوش ترتیب
پی دی اف درس ریاضیات گسسته
هر یک از فیلمهای درس یا حل تست ریاضیات گسسته را تهیه کنید در داشبورد پی دی اف مربوط به آن دوره نیز قرار میگیرد و دانشجویان براحتی میتوانند جزوات را پرینت و هنگام تماشای فیلمهای درس و حل تست ریاضیات گسسته از جزوات خط ببرند و مطالب مهم را هایلایت کنند و در صورت نیاز برای خودتان در کنار جزوات یاداشت برداری کنید.
منابع و مراجع
- 1. https://en.wikipedia.org/wiki/Four_color_theorem
- 2. https://en.wikipedia.org/wiki/David_Hilbert
- 3. https://plato.stanford.edu/entries/turing-machine/
فیلمهای رایگان
کتاب مرجع ریاضی گسسته چیست؟
مرجع اصلی ریاضیات گسسته کتاب گریمالدی است، پس از کتاب گریمالدی کتاب روزن نیز یکی از مراجع مهم ریاضیات گسسته است، تمامی این کتب مرجع را میتوانید بصورت رایگان در این صفحه دانلود کنید
کاربرد ریاضی گسسته در کامپیوتر چیست؟
مثال های بسیار زیادی در دنیا کامپیوتر وجود دارد که برای حل آن مسائل بر روی ریاضیات گسسته تمرکز میشود. ریاضی باینری در واقع ریاضیات گسسته است. پس اساس وجود کامپیوتر به ریاضیات گسسته وابسته است. نرم افزارها و فایلها هر دو به عنوان رشته های عظیمی از ۱ و ۰ ذخیره می شوند. به همین ترتیب شبکه های کامپیوتری نیز بر اساس ریاضیات گسسته توسعه یافته اند. سیم بندی های یک کامپیوتر معمولی خانگی با استفاده از کمترین میزان کابل ، در حقیقت مسئله درخت کم وزن است. گوگل مپ نیز از طرح چنین مسئله ای برای یافتن کوتاه ترین مسیر بهره می برد. در برنامه ریزی مسیر راه آهن از ریاضی گسسته استفاده می کند. تصمیم گیری در مورد نحوه گسترش خطوط ریلی قطار، برنامه ریزی و زمانبندی قطارها و حتی برنامه ریزی برای خدمه و تجهیزات برای سفرهای قطار، نیز از تئوری نمودار و از جبر خطی توأمان استفاده می کند. بدین ترتیب متوجه می شویم که ریاضیات گسسته بخش جدا نشدنی از زندگی روزمره ما است.
اهمیت درس ریاضی گسسته در رشته کامپیوتر چقدر است؟
ریاضیات گسسته یکی از مهم ترین دروس رشته کامپیوتر و همین طور کنکور ارشد کامپیوتر و آی تی است و تقریبا میتوان گفت که پیش نیاز تمامی دروس رشته کامپیوتر است و تک تک فصل های ریاضی گسسته در دروس دیگر کاربرد دارد بنابراین توصیه می شود که این درس را خوب فرا گیرید








































